No CrossRef data available.
Published online by Cambridge University Press: 25 February 2013
In this paper we consider the following ‘Toeplitz completion’ problem: Complete the unspecified analytic Toeplitz entries of the partial block Toeplitz matrix
to make A hyponormal, where ψi∈H∞ is a non-constant rational function for i=1,2.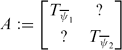 $
\begin{linenomath}
A:=\begin{bmatrix} T_{\overline\psi_1}& ?\\[4pt]
\T_{\overline\psi_2} \end{bmatrix}
\end{linenomath}
$
$
\begin{linenomath}
A:=\begin{bmatrix} T_{\overline\psi_1}& ?\\[4pt]
\T_{\overline\psi_2} \end{bmatrix}
\end{linenomath}
$