Hostname: page-component-f554764f5-rj9fg Total loading time: 0 Render date: 2025-04-15T11:58:56.203Z Has data issue: false hasContentIssue false
  • English
  • Français

A hyperbolic free-by-cyclic group determined by its finite quotients

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  04 April 2025

Naomi Andrew Open the ORCID record for Naomi Andrew [Opens in a new window] ,
Paige Hillen ,
Robert Alonzo Lyman Open the ORCID record for Robert Alonzo Lyman [Opens in a new window]  and
Catherine Eva Pfaff Open the ORCID record for Catherine Eva Pfaff [Opens in a new window]
Naomi Andrew
Affiliation:
Mathematical Institute, University of Oxford, Oxford, OX2 6GG, UK
Paige Hillen
Affiliation:
Department of Mathematics, University of California - Santa Barbara, Santa Barbara, 93117, USA
Robert Alonzo Lyman*
Affiliation:
Department of Mathematics, Rutgers University - Newark, Newark, NJ 07102, USA
Catherine Eva Pfaff
Affiliation:
Department of Mathematics & Statistics, Queen’s University, Kingston, ON K7L 3N6, Canada Institute for Advanced Study, Princeton, NJ 08540, USA
*
Corresponding author: Robert Alonzo Lyman; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the group 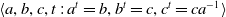$ \langle a,b,c,t \,:\, a^t=b,b^t=c,c^t=ca^{-1} \rangle$ is profinitely rigid amongst free-by-cyclic groups, providing the first example of a hyperbolic free-by-cyclic group with this property.

Keywords

free-by-cyclic grouphyperbolic groupprofinite rigidityresidual finitenessOut(F_n)

MSC classification

Primary: 20E26: Residual properties and generalizations; residually finite groups
Secondary: 20E05: Free nonabelian groups 20E36: Automorphisms of infinite groups 20F65: Geometric group theory
Type
Research Article
Information
Glasgow Mathematical Journal , First View , pp. 1 - 3
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Baumslag, G., Residually finite groups with the same finite images, Compos. Math. 29 (1974), 249–252.Google Scholar
Bridson, M. R. and Grunewald, F. J., Grothendieck’s problems concerning profinite completions and representations of groups, Ann. Math. 160(1) (2004), 359–373.CrossRefGoogle Scholar
Bridson, M. R., McReynolds, D. B., Reid, A. W. and Spitler, R., Absolute profinite rigidity and hyperbolic geometry, Ann. Math. 192(3) (2020), 679–719.CrossRefGoogle Scholar
Bogopolski, O., Martino, A. and Ventura, E., The automorphism group of a free-by-cyclic group in rank 2, Comm. Algebra 35(5) (2007), 1675–1690.CrossRefGoogle Scholar
Bridson, M. R. and Piwek, P., Profinite rigidity for free-by-cyclic groups with centre, September 2024. Preprint, available at arxiv: 2409.20513 [math.GR]Google Scholar
Bridson, M. R. and Reid, A. W., Profinite rigidity, fibering, and the figure-eight knot, in What’s next?—the mathematical legacy of William P. Thurston, Vol. 205 of Ann. of Math. Stud. (Princeton Univ. Press, Princeton, NJ, 2020), 45–64.Google Scholar
Brinkmann, P., Hyperbolic automorphisms of free groups, Geom. Funct. Anal. 10(5) (2000), 1071–1089.CrossRefGoogle Scholar
Bridson, M. R., Reid, A. W. and Wilton, H., Profinite rigidity and surface bundles over the circle, Bull. Lond. Math. Soc. 49(5) (2017), 831–841.CrossRefGoogle Scholar
Hillen, P., Latent symmetry of graphs and stretch factors in $\mathrm {Out}(F_r)$ , September 2024. Preprint, available at arxiv: 2409.19446 [math.GR]Google Scholar
Hughes, S. and Kudlinska, M., On profinite rigidity amongst free-by-cyclic groups I: the generic case, March 2023. Preprint, available at arxiv: 2303.16834 [math.GR].Google Scholar
Khukhro, E. I. and Mazurov, V. D., editors. The Kourovka Notebook: Unsolved Problems in Group Theory, Russian Institute of Mathematics, Academy of Sciences, Siberian Division, Novosibirsk, 2022. 22nd edition,Google Scholar
Platonov, V. P. and Tavgen, O. I., On the Gothendieck problem of profinite completions of groups, Dokl. Akad. Nauk SSSR 288(5) (1986), 1054–1058.Google Scholar
Reid, A. W., Profinite rigidity, in Proceedings of the international congress of mathematicians 2018, ICM 2018, Rio de Janeiro, Brazil, August 1--9, 2018, Vol. II. Invited lectures (World Scientific, Sociedade Brasileira de Matemática (SBM), Hackensack, NJ, Rio de Janeiro, 2018), 1193–1216.CrossRefGoogle Scholar