Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Snider, Robert L.
1983.
Group rings with finite endomorphism dimension.
Archiv der Mathematik,
Vol. 41,
Issue. 3,
p.
219.
Snider, Robert
2006.
Periodic groups whose simple modules have finite central endomorphism dimension.
Proceedings of the American Mathematical Society,
Vol. 134,
Issue. 12,
p.
3485.


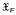 the class of all groups
the class of all groups 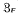 the class of all groups G such that every irreducible FG-module has finite dimension over its endomorphism ring. Clearly
the class of all groups G such that every irreducible FG-module has finite dimension over its endomorphism ring. Clearly 
