Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T19:57:13.614Z Has data issue: false hasContentIssue false
  • English
  • Français

THE GROUP OF AUTOMORPHISMS OF THE FIRST WEYL ALGEBRA IN PRIME CHARACTERISTIC AND THE RESTRICTION MAP

Published online by Cambridge University Press:  01 May 2009

V. V. BAVULA
V. V. BAVULA*
Affiliation:
Department of Pure Mathematics, University of Sheffield, Hicks Building, Sheffield S3 7RH, United Kingdom e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

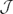Let K be a perfect field of characteristic p > 0; A1 := K〈x, ∂|∂x−x∂=1〉 be the first Weyl algebra; and Z:=K[X:=xp, Y:=∂p] be its centre. It is proved that (i) the restriction map res : AutK(A1)→ AutK(Z), σ ↦ σ|Z is a monomorphism with im(res) = Γ := {τ ∈ AutK(Z)|(τ)=1}, where 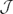(τ) is the Jacobian of τ, (Note that AutK(Z)=K* ⋉ Γ, and if K is not perfect then im(res) ≠ Γ.); (ii) the bijection res : AutK(A1) → Γ is a monomorphism of infinite dimensional algebraic groups which is not an isomorphism (even if K is algebraically closed); (iii) an explicit formula for res−1 is found via differential operators 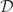(Z) on Z and negative powers of the Fronenius map F. Proofs are based on the following (non-obvious) equality proved in the paper:

Keywords

14J5016W2014L1714R1014R1514M20
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 2 , May 2009 , pp. 263 - 274
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Adjamagbo, K. and van den Essen, A., On equivalence of the Jacobian, Dixmier and Poisson Conjectures in any characteristic, arXiv:math. AG/0608009.Google Scholar
2.Belov-Kanel, A. and Kontsevich, M., The Jacobian conjecture is stably equivalent to the Dixmier Conjecture, Mosc. Math. J. 7 (2) (2007), 209–218, arXiv:math. RA/0512171.CrossRefGoogle Scholar
3.Belov-Kanel, A. and Kontsevich, M., Automorphisms of the Weyl algebra, Lett. Math. Phys. 74 (2) (2005), 181–199, arXiv:math. RA/0512169.CrossRefGoogle Scholar
4.Dixmier, J., Sur les algèbres de Weyl, Bull. Soc. Math. France 96 (1968), 209–242.CrossRefGoogle Scholar
5.Jung, H. W. E., Uber ganze birationale Transformationen der Eben, J. Reiner Angew. Math. 184 (1942), 161–174.CrossRefGoogle Scholar
6.Humphreys, J. E., Linear Algebraic Groups, (Springer-Verlag, 1975).CrossRefGoogle Scholar
7.Van der Kulk, W., On polynomial ring in two variables, Niew. Arch. Wisk. 1 (1953), 33–41.Google Scholar
8.Makar-Limanov, L., On automorphisms of Weyl algebra, Bull. Soc. Math. France 112 (1984), 359–363.CrossRefGoogle Scholar
9.Kambayashi, T., Some results on pro-affine algebras and ind-affine schemes, Osaka J. Math. 40 (2003), 621–638.Google Scholar
10.Shafarevich, I. R., On some infinite-dimensional groups, Rend. Mat. Appl. 25 (1966), 208–212.Google Scholar
11.Shafarevich, I. R., On some infinite-dimensional groups-II, Math. USSR-Izvestija 18 (1982), 185–194.CrossRefGoogle Scholar
12.Tsuchimoto, Y., Endomorphisms of Weyl algebra and p-curvatures. Osaka J. Math. 42 (2) (2005), 435–452.Google Scholar