No CrossRef data available.
Article contents
Grothendieck groups of twisted free associative algebras
Published online by Cambridge University Press: 18 May 2009
Extract
Let R be an associative ring with identity, X a set of noncommuting variables, 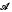 = {αx} x ∈ X a set of automorphisms αx of R and R
= {αx} x ∈ X a set of automorphisms αx of R and R {X} the
{X} the 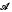 -twisted free associative algebra on X over R. Let Y be another set of noncommuting variables, ℬ = {βy}y∈Y a set of automorphisms βy of R
-twisted free associative algebra on X over R. Let Y be another set of noncommuting variables, ℬ = {βy}y∈Y a set of automorphisms βy of R {X} and S = (R
{X} and S = (R {X})ℬ {Y} the ℬ-twisted free associative algebra on Y over R
{X})ℬ {Y} the ℬ-twisted free associative algebra on Y over R {X}. Next, let X1 be a set of noncommuting variables, for each l = 1,2,…. We form the free associative algebra S1 = S{X1}on Xl over S and inductively, we form the free associative algebra Sl+1 = Sl{Xl+1} on Xl+1 over Sl, l = 1,2,….
{X}. Next, let X1 be a set of noncommuting variables, for each l = 1,2,…. We form the free associative algebra S1 = S{X1}on Xl over S and inductively, we form the free associative algebra Sl+1 = Sl{Xl+1} on Xl+1 over Sl, l = 1,2,….
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1977


