Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T22:22:16.408Z Has data issue: false hasContentIssue false
  • English
  • Français

GORENSTEIN AND Sr PATH IDEALS OF CYCLES

Published online by Cambridge University Press:  26 August 2014

DARIUSH KIANI ,
SARA SAEEDI MADANI  and
NAOKI TERAI
DARIUSH KIANI
Affiliation:
Department of Pure Mathematics, Faculty of Mathematics and Computer Science, Amirkabir University of Technology (Tehran Polytechnic), 424, Hafez Ave., Tehran 15914, Iran, and School of Mathematics, Institute for Research in Fundamental Sciences (IPM), Tehran, Iran e-mail: [email protected], [email protected]
SARA SAEEDI MADANI
Affiliation:
e-mail: [email protected]
NAOKI TERAI
Affiliation:
Naoki Terai, Department of Mathematics, Faculty of Culture and Education, Saga University, Saga 840-8502, Japan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R = k[x1,…,xn], where k is a field. The path ideal (of length t ≥ 2) of a directed graph G is the monomial ideal, denoted by It(G), whose generators correspond to the directed paths of length t in G. Let Cn be an n-cycle. We show that R/It(Cn) is Sr if and only if it is Cohen-Macaulay or 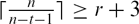$\lceil \frac{n}{n-t-1}\rceil\geq r+3$. In addition, we prove that R/It(Cn) is Gorenstein if and only if n = t or 2t + 1. Also, we determine all ordinary and symbolic powers of It(Cn) which are Cohen-Macaulay. Finally, we prove that It(Cn) has a linear resolution if and only if t ≥ n − 2.

Keywords

13D0213F5505C7505C38
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 57 , Issue 1 , January 2015 , pp. 7 - 15
Copyright
Copyright © Glasgow Mathematical Journal Trust 2014 

References

REFERENCES

1.Barile, M. and Terai, N., Arithmetical ranks of Stanley–Reisner ideals of simplicial complexes with a cone. Comm. Algebra 38 (10) (2010), 3686–3698.CrossRefGoogle Scholar
2.Brumatti, P. and da Silva, A.F., On the symmetric and Rees algebras of (n,k)-cyclic ideals. 16th School of Algebra, Part II, Brasilia, Brazil, 2000 (Portuguese). Mat. Contemp. 21 (2001), 27–42.Google Scholar
3.Bruns, W. and Herzog, J., Cohen–Macaulay rings. Cambridge Studies in Advanced Mathematics, vol. 39 (Cambridge University Press, Cambridge, UK, 1993).Google Scholar
4.Conca, A. and Negri, De, M-sequences, graph ideals and ladder ideals of linear type, J. Algebra 211 (2) (1999), 599–624.CrossRefGoogle Scholar
5.Eagon, J. A. and Reiner, V., Resolutions of Stanely–Reisner rings and Alexander duality. J. Pure Appl. Algebra 130 (1998), 265–275.CrossRefGoogle Scholar
6.Hà, H. T. and Van Tuyl, A., Monomial ideals, edge ideals of hypergraphs, and their graded Betti numbers. J. Algebraic Combin. 27 (2) (2008), 215–245.Google Scholar
7.Haghighi, H., Terai, N., Yassemi, S. and Zaare-Nahandi, R., Sequentially Sr simplicial complexes and sequentially S 2 graphs, Proc. Amer. Math. Soc. 139 (6) (2011), 1993–2005.Google Scholar
8.Hegedüs, G., Betti numbers of Stanley–Reisner rings with pure resolutions. arXiv. math.AC/1101.5565v1 (2011).Google Scholar
9.Herzog, J. and Hibi, T., Monomial ideals (Springer, New York, NY, 2010).Google Scholar
10.Rinaldo, G., Terai, N. and Yoshida, K., On the second powers of Stanley–Reisner ideals, J. Commut. Algebra 3 (3) (2011), 405–430.Google Scholar
11.Saeedi Madani, S. and Kiani, D., Cohen–Macaulay and Gorenstein path ideals of trees, Algebra Colloq. (to appear).Google Scholar
12.Saeedi Madani, S., Kiani, D. and Terai, Naoki, Sequentially Cohen–Macaulay path ideals of cycles, Bull. Math. Soc. Sci. Math. Roumanie 54 (102) No. 4 (2011), 353–363.Google Scholar
13.Terai, N. and Trung, N. V., Cohen–Macaulayness of large powers of Stanley–Reianer ideals. arXiv. math.AC/1009.0833v1 (2010).Google Scholar
14.Villarreal, R. H., Monomial algebras (Marcel Dekker, New York, NY, 2001).Google Scholar
15.Yanagawa, K., Alexander duality for Stanley–Reisner rings and squarefree ℕn-graded modules, J. Algebra 225 (2000), 630–645.Google Scholar