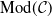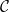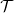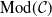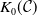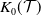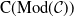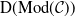1. Introduction
Tilting theory arises as a universal method for constructing equivalences between categories. Since its advent, it has been an essential tool in the study of many areas of mathematics, including algebraic group theory, commutative and noncommutative algebraic geometry, and algebraic topology.
Tilting theory can trace its history back to the article by Bernstein et al. [Reference Bernstein, Gelfand and Ponomarev8], where they used reflection functors to construct recursively all the indecomposable modules from simple modules over a representation-finite hereditary algebra. The major milestone in the development of tilting theory was the article by Brenner and Butler [Reference Brenner and Butler9]. They introduced the notion of a tilting module over a finite dimensional algebra and established the so-called Brenner–Butler theorem by a tilting module. In this article, the behavior of the associated quadratic forms was investigated as well. Dropping a more restrictive notion of tilting module defined by Brenner and Butler, Happel and Ringel [Reference Happel and Ringel15] successfully simplified the definition of original tilting modules. A few years later, Miyashita [Reference Miyashita26] generalized the concept of tilting modules allowing modules of any finite projective dimension and over any ring, for which a generalization of the Brenner–Butler theorem was still valid. Indeed, the authors, like Brenner and Butler [Reference Brenner and Butler9], Happel and Ringel [Reference Happel and Ringel15], and Miyashita [Reference Miyashita26], considered finitely generated tilting modules, obtaining portions of the Brenner–Butler theorem. Colpi and Trlifaj [Reference Colpi and Trlifaj10] generalized the notion of tilting module to not necessarily finitely generated modules. Later on, Angeleri-Hügel and Coelho [Reference Angeleri-Hügel and Coelho1] did the same with the concept of Miyashita.
On the other hand, functor categories, introduced by Auslander [Reference Auslander2], are used as a potent tool for solving some important problems in representation theory. Martsinkovsky and Russell have studied the injective stabilization of additive functors (see [Reference Martsinkovsky and Russell23–Reference Martsinkovsky and Russell25]). Recently, Martínez-Villa and Ortiz-Morales [Reference Martínez-Villa and Ortiz-Morales20–Reference Martínez-Villa and Ortiz-Morales22] initialed the study of tilting theory in arbitrary functor categories with applications to the functor category Mod(
![]() $\mathcal{A}$
) for
$\mathcal{A}$
) for
![]() $\mathcal{A}$
a category of modules over a finite dimensional algebra. The first one [Reference Martínez-Villa and Ortiz-Morales20] in a series of three is to deal with the concept of tilting subcategory
$\mathcal{A}$
a category of modules over a finite dimensional algebra. The first one [Reference Martínez-Villa and Ortiz-Morales20] in a series of three is to deal with the concept of tilting subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, which is the category of contravariant functors from a skeletally small additive category
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, which is the category of contravariant functors from a skeletally small additive category
![]() $\mathcal{C}$
, to the category of abelian groups. They showed that the Brenner and Butler theorem holds for
$\mathcal{C}$
, to the category of abelian groups. They showed that the Brenner and Butler theorem holds for
![]() $\mathcal{T}$
. In the second and third papers [Reference Martínez-Villa and Ortiz-Morales21, Reference Martínez-Villa and Ortiz-Morales22], replacing a tilting subcategory with a generalized tilting subcategory
$\mathcal{T}$
. In the second and third papers [Reference Martínez-Villa and Ortiz-Morales21, Reference Martínez-Villa and Ortiz-Morales22], replacing a tilting subcategory with a generalized tilting subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, they continued the project of extending tilting theory to the same functor category with particular focusing on the equivalence of the derived categories of bounded complexes
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, they continued the project of extending tilting theory to the same functor category with particular focusing on the equivalence of the derived categories of bounded complexes
![]() $\mathop{\textrm{D}}\nolimits ^b\!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
and
$\mathop{\textrm{D}}\nolimits ^b\!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
and
![]() $\mathop{\textrm{D}}\nolimits ^b\!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{T}))$
.
$\mathop{\textrm{D}}\nolimits ^b\!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{T}))$
.
In the same spirit as in the above-mentioned results of Martínez-Villa and Ortiz-Morales, in this paper, we aim at extending some well-known results, relating generalized tilting modules in module category, to a generalized tilting subcategory of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. We now give a brief outline of the contents of this paper.
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. We now give a brief outline of the contents of this paper.
In Section 2, we collect preliminary notions and results on functor categories that will be useful throughout the paper and we fix notation. We also give an example of a generalized tilting subcategory of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
(see Example 2.4).
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
(see Example 2.4).
In Section 3, we are interested in studying a generalized version of the Brenner–Butler theorem in functor category. More precisely, we show in Theorem 3.4 that for a generalized tilting subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
one gets an equivalence between the categories
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
one gets an equivalence between the categories
![]() $\mathop{\textrm{KE}}\nolimits ^{\infty }_e\!(\mathcal{T})$
and
$\mathop{\textrm{KE}}\nolimits ^{\infty }_e\!(\mathcal{T})$
and
![]() $\mathop{\textrm{KT}}\nolimits ^{\infty }_e\!(\mathcal{T})$
. As an application of this main theorem, we state in Theorem 3.8 that if
$\mathop{\textrm{KT}}\nolimits ^{\infty }_e\!(\mathcal{T})$
. As an application of this main theorem, we state in Theorem 3.8 that if
![]() $\mathcal{C}$
is an abelian category with enough injectives and
$\mathcal{C}$
is an abelian category with enough injectives and
![]() $\mathcal{T}$
is an
$\mathcal{T}$
is an
![]() $n$
-tilting subcategory of
$n$
-tilting subcategory of
![]() $\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
with pseudokernels, then the Grothendieck groups
$\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
with pseudokernels, then the Grothendieck groups
![]() $K_0(\mathcal{C})$
and
$K_0(\mathcal{C})$
and
![]() $K_0(\mathcal{T})$
are isomorphic.
$K_0(\mathcal{T})$
are isomorphic.
In Section 4, we prove in Theorem 4.3 that for a generalized tilting subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
,
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
,
![]() $(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}),\mathcal{T}^{\perp _{\infty }})$
is a hereditary and complete cotorsion pair. Furthermore, this induces an abelian model structure on
$(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}),\mathcal{T}^{\perp _{\infty }})$
is a hereditary and complete cotorsion pair. Furthermore, this induces an abelian model structure on
![]() $\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
, where the trivial objects are the exact complexes, the cofibrant objects are
$\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
, where the trivial objects are the exact complexes, the cofibrant objects are
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})}$
complexes, and the class of fibrant objects is given by the complexes whose terms are in
$\mathcal{^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})}$
complexes, and the class of fibrant objects is given by the complexes whose terms are in
![]() $\mathcal{T}^{\perp _{\infty }}$
(see Corollary 4.6).
$\mathcal{T}^{\perp _{\infty }}$
(see Corollary 4.6).
In Section 5, we use the model structure on
![]() $\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
to describe the t-structure on the derived category
$\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
to describe the t-structure on the derived category
![]() $\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
, induced by a generalized tilting subcategory
$\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
, induced by a generalized tilting subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
(see Theorem 5.5).
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
(see Theorem 5.5).
2. Preliminaries
Throughout this paper,
![]() $\mathcal{C}$
will be an arbitrary skeletally small additive category, and
$\mathcal{C}$
will be an arbitrary skeletally small additive category, and
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
will denote the category of additive contravariant functors from
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
will denote the category of additive contravariant functors from
![]() $\mathcal{C}$
to the category of abelian groups. It follows from [Reference Prest28, Theorem 1.2 and Proposition 1.9] or [Reference Martínez-Villa and Ortiz-Morales20, Section 1.2] that
$\mathcal{C}$
to the category of abelian groups. It follows from [Reference Prest28, Theorem 1.2 and Proposition 1.9] or [Reference Martínez-Villa and Ortiz-Morales20, Section 1.2] that
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
is a Grothendieck category with enough projective objects. In addition,
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
is a Grothendieck category with enough projective objects. In addition,
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
also has enough injective objects by [Reference Jensen and Lenzing19, p.384, Theorem B.3]. If
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
also has enough injective objects by [Reference Jensen and Lenzing19, p.384, Theorem B.3]. If
![]() $M,N\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, we denote the set
$M,N\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, we denote the set
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})(M,N)$
of natural transformations
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})(M,N)$
of natural transformations
![]() $M\to N$
by
$M\to N$
by
![]() ${\textrm{Hom}}_{\mathcal{C}}(M,N)$
. Following [Reference Auslander3], a functor
${\textrm{Hom}}_{\mathcal{C}}(M,N)$
. Following [Reference Auslander3], a functor
![]() $F$
is called representable if it is isomorphic to
$F$
is called representable if it is isomorphic to
![]() $\mathcal{C}(\,\,\,\,,C)$
for some
$\mathcal{C}(\,\,\,\,,C)$
for some
![]() $C\in \mathcal{C}$
. A functor
$C\in \mathcal{C}$
. A functor
![]() $F$
is finitely generated if there is an epimorphism
$F$
is finitely generated if there is an epimorphism
![]() $\mathcal{C}(\,\,\,\,,C)\to F\to 0$
with
$\mathcal{C}(\,\,\,\,,C)\to F\to 0$
with
![]() $C\in \mathcal{C}$
. A functor
$C\in \mathcal{C}$
. A functor
![]() $F$
is finitely presented, if there exists a sequence of natural transformations
$F$
is finitely presented, if there exists a sequence of natural transformations
![]() $\mathcal{C}(\,\,\,\,,C_1)\to \mathcal{C}(\,\,\,\,,C_0)\to F\to 0$
with
$\mathcal{C}(\,\,\,\,,C_1)\to \mathcal{C}(\,\,\,\,,C_0)\to F\to 0$
with
![]() $C_0, C_1\in \mathcal{C}$
such that for any
$C_0, C_1\in \mathcal{C}$
such that for any
![]() $C\in \mathcal{C}$
the sequence of abelian groups
$C\in \mathcal{C}$
the sequence of abelian groups
![]() $\mathcal{C}(C,C_1)\to \mathcal{C}(C,C_0)\to F(C)\to 0$
is exact. We denote by mod(
$\mathcal{C}(C,C_1)\to \mathcal{C}(C,C_0)\to F(C)\to 0$
is exact. We denote by mod(
![]() $\mathcal{C}$
) the full subcategory of
$\mathcal{C}$
) the full subcategory of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
consisting of finitely presented functors. An object
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
consisting of finitely presented functors. An object
![]() $P$
in
$P$
in
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
is projective (finitely generated projective) if and only if
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
is projective (finitely generated projective) if and only if
![]() $P$
is a summand of
$P$
is a summand of
![]() $\coprod _{i\in I}\mathcal{C}(\,\,\,\,,C_i)$
for a (finite) family
$\coprod _{i\in I}\mathcal{C}(\,\,\,\,,C_i)$
for a (finite) family
![]() $\{{C_i}\}_{i\in I}$
of objects in
$\{{C_i}\}_{i\in I}$
of objects in
![]() $\mathcal{C}$
(see [Reference Martínez-Villa and Ortiz-Morales20, Paragraph 3 of Section 1.2]). We recall from [Reference Auslander3, p.188] that an annuli variety is a skeletally small additive category in which idempotents split.
$\mathcal{C}$
(see [Reference Martínez-Villa and Ortiz-Morales20, Paragraph 3 of Section 1.2]). We recall from [Reference Auslander3, p.188] that an annuli variety is a skeletally small additive category in which idempotents split.
Let
![]() $\mathcal{A}$
be an abelian category and
$\mathcal{A}$
be an abelian category and
![]() $F\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{A})$
, then there is an exact sequence
$F\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{A})$
, then there is an exact sequence
![]() $\mathcal{A}(\,\,\,\,,X)\buildrel{(\,\,\,\,,f)} \over \longrightarrow \mathcal{A}(\,\,\,\,,Y)\buildrel{} \over \longrightarrow F\to 0$
, the value of
$\mathcal{A}(\,\,\,\,,X)\buildrel{(\,\,\,\,,f)} \over \longrightarrow \mathcal{A}(\,\,\,\,,Y)\buildrel{} \over \longrightarrow F\to 0$
, the value of
![]() $v$
at
$v$
at
![]() $F$
is defined by the following exact sequence
$F$
is defined by the following exact sequence
![]() $X\buildrel{f} \over \longrightarrow Y\to v(F)\to 0$
. This assignment extends to the defect functor
$X\buildrel{f} \over \longrightarrow Y\to v(F)\to 0$
. This assignment extends to the defect functor
![]() $v$
:
$v$
:
![]() $\mathop{\textrm{mod}}\nolimits \!(\mathcal{A})\to \mathcal{A}$
.
$\mathop{\textrm{mod}}\nolimits \!(\mathcal{A})\to \mathcal{A}$
.
Lemma 2.1.
Let
![]() $\mathcal{C}$
be an annuli variety and
$\mathcal{C}$
be an annuli variety and
![]() $\mathcal{T}$
a skeletally small full subcategory of
$\mathcal{T}$
a skeletally small full subcategory of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. We define the following functor:
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. We define the following functor:
where the contravariant functor
![]() ${\textrm{Hom}}(\,\,\,\,,M)_{\mathcal{T}}\,:\, \mathcal{T}\to{\bf Ab}$
is given by
${\textrm{Hom}}(\,\,\,\,,M)_{\mathcal{T}}\,:\, \mathcal{T}\to{\bf Ab}$
is given by
![]() ${\textrm{Hom}}(\,\,\,\,,M)_{\mathcal{T}}(T)={\textrm{Hom}}(T,M)$
for any
${\textrm{Hom}}(\,\,\,\,,M)_{\mathcal{T}}(T)={\textrm{Hom}}(T,M)$
for any
![]() $T\in \mathcal{T}$
. Then the following statements hold.
$T\in \mathcal{T}$
. Then the following statements hold.
-
(1) The functor
 $\phi$
has a left adjoint
$\phi$
has a left adjoint
 $-\otimes \mathcal{T}\,:\, \mathop{\textrm{Mod}}\nolimits \!(\mathcal{T}) \to \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
$-\otimes \mathcal{T}\,:\, \mathop{\textrm{Mod}}\nolimits \!(\mathcal{T}) \to \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. -
(2)
 $\mathcal{T}(\,\,\,\,,T)\otimes \mathcal{T}=T$
for any
$\mathcal{T}(\,\,\,\,,T)\otimes \mathcal{T}=T$
for any
 $T\in \mathcal{T}$
.
$T\in \mathcal{T}$
. -
(3)
 $-\otimes \mathcal{T}|_{\mathop{\textrm{mod}}\nolimits \!(\mathcal{T})}=v$
.
$-\otimes \mathcal{T}|_{\mathop{\textrm{mod}}\nolimits \!(\mathcal{T})}=v$
.
Proof. (1) and (2) come from [Reference Martínez-Villa and Ortiz-Morales21, Theorem 3] and [Reference Martínez-Villa and Ortiz-Morales20, Remark 1], respectively.
(3) It suffices to show that
![]() $(v,\phi )$
is an adjoint pair. Let
$(v,\phi )$
is an adjoint pair. Let
![]() $M\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
and
$M\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
and
![]() $N\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, we need to find an isomorphism
$N\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, we need to find an isomorphism
which is natural in both
![]() $M$
and
$M$
and
![]() $N$
. Suppose that there is an exact sequence
$N$
. Suppose that there is an exact sequence
![]() $\mathcal{T}(\,\,\,\,,T_1)\buildrel{} \over \longrightarrow \mathcal{T}(\,\,\,\,,T_0)\buildrel{} \over \longrightarrow M\to 0$
with
$\mathcal{T}(\,\,\,\,,T_1)\buildrel{} \over \longrightarrow \mathcal{T}(\,\,\,\,,T_0)\buildrel{} \over \longrightarrow M\to 0$
with
![]() $T_1, T_0\in \mathcal{T}$
. By the construction of defect functor, we get an exact sequence
$T_1, T_0\in \mathcal{T}$
. By the construction of defect functor, we get an exact sequence
![]() $T_1\buildrel{f} \over \longrightarrow T_0\to v(M)\to 0$
in
$T_1\buildrel{f} \over \longrightarrow T_0\to v(M)\to 0$
in
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. It follows from the Yoneda Lemma that
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. It follows from the Yoneda Lemma that
![]() $(\mathcal{T}(\,\,\,\,,T_1), \phi (N))\cong (T_1, N)$
and
$(\mathcal{T}(\,\,\,\,,T_1), \phi (N))\cong (T_1, N)$
and
![]() $(\mathcal{T}(\,\,\,\,,T_0), \phi (N))\cong (T_0, N)$
. Then we have the following commutative diagram with exact rows
$(\mathcal{T}(\,\,\,\,,T_0), \phi (N))\cong (T_0, N)$
. Then we have the following commutative diagram with exact rows

So
![]() $\theta$
is an isomorphism and it is easy to check that
$\theta$
is an isomorphism and it is easy to check that
![]() $\theta$
is natural in both
$\theta$
is natural in both
![]() $M$
and
$M$
and
![]() $N$
.
$N$
.
Following [Reference Martínez-Villa and Ortiz-Morales20] and [Reference Martínez-Villa and Ortiz-Morales21], given categories
![]() $\mathcal{C}$
and
$\mathcal{C}$
and
![]() $\mathcal{T}$
as in Lemma 2.1, since
$\mathcal{T}$
as in Lemma 2.1, since
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
and
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
and
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{T})$
have enough projective and injective objects, we can define the
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{T})$
have enough projective and injective objects, we can define the
![]() $n$
th right derived functors of the functors
$n$
th right derived functors of the functors
![]() ${\textrm{Hom}}_{\mathcal{C}}(M,\,\,\,\,)$
and
${\textrm{Hom}}_{\mathcal{C}}(M,\,\,\,\,)$
and
![]() ${\textrm{Hom}}_{\mathcal{C}}(\,\,\,\,,N)$
, which will be denoted by
${\textrm{Hom}}_{\mathcal{C}}(\,\,\,\,,N)$
, which will be denoted by
![]() ${\textrm{Ext}}^n_{\mathcal{C}}(M,\,\,\,\,)$
and
${\textrm{Ext}}^n_{\mathcal{C}}(M,\,\,\,\,)$
and
![]() ${\textrm{Ext}}^n_{\mathcal{C}}(\,\,\,\,,N)$
, respectively.
${\textrm{Ext}}^n_{\mathcal{C}}(\,\,\,\,,N)$
, respectively.
In the same way, the functor
![]() $\phi \,:\, \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})\to \mathop{\textrm{Mod}}\nolimits \!(\mathcal{T})$
has an
$\phi \,:\, \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})\to \mathop{\textrm{Mod}}\nolimits \!(\mathcal{T})$
has an
![]() $n$
th right derived functor, denoted by
$n$
th right derived functor, denoted by
![]() ${\textrm{Ext}}^n_{\mathcal{C}}(\,\,\,\,,-)_{\mathcal{T}}$
, and they are defined as
${\textrm{Ext}}^n_{\mathcal{C}}(\,\,\,\,,-)_{\mathcal{T}}$
, and they are defined as
![]() ${\textrm{Ext}}^n_{\mathcal{C}}(\,\,\,\,,-)_{\mathcal{T}}(M)={\textrm{Ext}}^n_{\mathcal{C}}(\,\,\,\,,M)_{\mathcal{T}}$
. Analogously, the functor
${\textrm{Ext}}^n_{\mathcal{C}}(\,\,\,\,,-)_{\mathcal{T}}(M)={\textrm{Ext}}^n_{\mathcal{C}}(\,\,\,\,,M)_{\mathcal{T}}$
. Analogously, the functor
![]() $-\otimes \mathcal{T}\,:\, \mathop{\textrm{Mod}}\nolimits \!(\mathcal{T}) \to \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
has an
$-\otimes \mathcal{T}\,:\, \mathop{\textrm{Mod}}\nolimits \!(\mathcal{T}) \to \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
has an
![]() $n$
th left derived functor, denoted by
$n$
th left derived functor, denoted by
![]() $\textrm{Tor}_n^{\mathcal{T}}(\,\,\,\,,\mathcal{T})$
.
$\textrm{Tor}_n^{\mathcal{T}}(\,\,\,\,,\mathcal{T})$
.
Let
![]() $\mathcal{T}$
be a subcategory of
$\mathcal{T}$
be a subcategory of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
![]() $\mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
(resp.
$\mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
(resp.
![]() $\mathop{\textrm{add}}\nolimits \!(\mathcal{T})$
) will denote the class of functors isomorphic to summands of (finite) direct sums of objects in
$\mathop{\textrm{add}}\nolimits \!(\mathcal{T})$
) will denote the class of functors isomorphic to summands of (finite) direct sums of objects in
![]() $\mathcal{T}$
and
$\mathcal{T}$
and
![]() $\mathop{\textrm{Gen}}\nolimits _n\!(\mathcal{T}$
) will denote the full subcategory consisting of
$\mathop{\textrm{Gen}}\nolimits _n\!(\mathcal{T}$
) will denote the full subcategory consisting of
![]() $M\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
for which there exists an exact sequence of the form
$M\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
for which there exists an exact sequence of the form
![]() $T_n\to \cdots \to T_2\to T_1\to M\to 0$
with
$T_n\to \cdots \to T_2\to T_1\to M\to 0$
with
![]() $T_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
. For any
$T_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
. For any
![]() $i\geqslant 1$
, we write
$i\geqslant 1$
, we write
We denote by
![]() $_{\mathcal{T}}\mathcal{X}$
the full subcategory of
$_{\mathcal{T}}\mathcal{X}$
the full subcategory of
![]() $\mathcal{T}^{\perp _{\infty }}$
consisting of functors
$\mathcal{T}^{\perp _{\infty }}$
consisting of functors
![]() $M$
such that there is an exact sequence of the form
$M$
such that there is an exact sequence of the form
![]() $\cdots \buildrel{f_{2}} \over \longrightarrow T_1\buildrel{f_{1}} \over \longrightarrow T_0\buildrel{f_{0}} \over \longrightarrow M\to 0$
with
$\cdots \buildrel{f_{2}} \over \longrightarrow T_1\buildrel{f_{1}} \over \longrightarrow T_0\buildrel{f_{0}} \over \longrightarrow M\to 0$
with
![]() $T_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
and
$T_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
and
![]() ${\textrm{Im}} \,f_i\in{\mathcal{T}^{\perp _{\infty }}}$
. It is easy to see that objects in
${\textrm{Im}} \,f_i\in{\mathcal{T}^{\perp _{\infty }}}$
. It is easy to see that objects in
![]() $_{\mathcal{T}}\mathcal{X}$
are in
$_{\mathcal{T}}\mathcal{X}$
are in
![]() $\mathop{\textrm{Gen}}\nolimits _n\!(\mathcal{T}$
) for each
$\mathop{\textrm{Gen}}\nolimits _n\!(\mathcal{T}$
) for each
![]() $n$
.
$n$
.
Next we recall the concept of cotorsion pairs in abelian categories, due to Holm and Jørgensen [Reference Holm and Jørgensen16, Section 6].
Definition 2.2.
Let
![]() $\mathcal{A},\mathcal{B}$
be two classes in
$\mathcal{A},\mathcal{B}$
be two classes in
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
-
(1) The pair
 $(\mathcal{A},\mathcal{B})$
is called a cotorsion pair if
$(\mathcal{A},\mathcal{B})$
is called a cotorsion pair if
 ${\mathcal{A}^{\perp _1}}=\mathcal{B}$
and
${\mathcal{A}^{\perp _1}}=\mathcal{B}$
and
 ${^{\perp _1}\mathcal{B}}=\mathcal{A}$
.
${^{\perp _1}\mathcal{B}}=\mathcal{A}$
. -
(2) A cotorsion pair
 $(\mathcal{A},\mathcal{B})$
is generated by a class
$(\mathcal{A},\mathcal{B})$
is generated by a class
 $\mathcal{X}$
of objects if
$\mathcal{X}$
of objects if
 ${\mathcal{X}^{\perp _1}}=\mathcal{B}$
.
${\mathcal{X}^{\perp _1}}=\mathcal{B}$
. -
(3) A cotorsion pair
 $(\mathcal{A},\mathcal{B})$
has enough projectives, that is, for every
$(\mathcal{A},\mathcal{B})$
has enough projectives, that is, for every
 $M\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
there exists an exact sequence
$M\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
there exists an exact sequence
 $0 \to B \to A \to M \to 0$
with
$0 \to B \to A \to M \to 0$
with
 $A\in \mathcal{A}$
and
$A\in \mathcal{A}$
and
 $B\in \mathcal{B}$
. Dually, we say that a cotorsion pair
$B\in \mathcal{B}$
. Dually, we say that a cotorsion pair
 $(\mathcal{A},\mathcal{B})$
has enough injectives, that is, for every
$(\mathcal{A},\mathcal{B})$
has enough injectives, that is, for every
 $M\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
there exists an exact sequence
$M\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
there exists an exact sequence
 $0\to M \to B \to A \to 0$
with
$0\to M \to B \to A \to 0$
with
 $A\in \mathcal{A}$
and
$A\in \mathcal{A}$
and
 $B\in \mathcal{B}$
.
$B\in \mathcal{B}$
. -
(4) A cotorsion pair
 $(\mathcal{A},\mathcal{B})$
is complete when it has enough injectives and enough projectives.
$(\mathcal{A},\mathcal{B})$
is complete when it has enough injectives and enough projectives.
-
(5) A cotorsion pair
 $(\mathcal{A},\mathcal{B})$
is hereditary if
$(\mathcal{A},\mathcal{B})$
is hereditary if
 ${\mathcal{A}^{\perp _{\infty }}}=\mathcal{B}$
and
${\mathcal{A}^{\perp _{\infty }}}=\mathcal{B}$
and
 ${^{\perp _{\infty }}\mathcal{B}}=\mathcal{A}$
.
${^{\perp _{\infty }}\mathcal{B}}=\mathcal{A}$
.
Now we will introduce the notion of a generalized tilting subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
Definition 2.3. ([Reference Martínez-Villa and Ortiz-Morales21, Definition 6]). Let
![]() $\mathcal{C}$
be an annuli variety. A full subcategory
$\mathcal{C}$
be an annuli variety. A full subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
is generalized tilting if the following statements (1)–(3) hold.
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
is generalized tilting if the following statements (1)–(3) hold.
-
(1) There exists a fixed integer
 $n$
such that every object
$n$
such that every object
 $T$
in
$T$
in
 $\mathcal{T}$
has a projective resolution
with each
$\mathcal{T}$
has a projective resolution
with each \begin{equation*}0\to P_n\to \cdots \to P_{1}\to P_{0}\to T\to 0,\end{equation*}
\begin{equation*}0\to P_n\to \cdots \to P_{1}\to P_{0}\to T\to 0,\end{equation*}
 $P_i$
finitely generated.
$P_i$
finitely generated.
-
(2) For each pair of objects
 $T$
and
$T$
and
 $T^{\prime}$
in
$T^{\prime}$
in
 $\mathcal{T}$
and any positive integer
$\mathcal{T}$
and any positive integer
 $i$
, we have
$i$
, we have
 ${\textrm{Ext}}^i_{\mathcal{C}}(T,T^{\prime})=0$
.
${\textrm{Ext}}^i_{\mathcal{C}}(T,T^{\prime})=0$
. -
(3) For each representable functor
 $\mathcal{C}(\,\,\,\,,C)$
, there is an exact sequence
with
$\mathcal{C}(\,\,\,\,,C)$
, there is an exact sequence
with \begin{equation*}0\to \mathcal {C}(\,\,\,\,,C)\to T^0_C\to \cdots \to T^{m_c}_C\to 0,\end{equation*}
\begin{equation*}0\to \mathcal {C}(\,\,\,\,,C)\to T^0_C\to \cdots \to T^{m_c}_C\to 0,\end{equation*}
 $T^i_C$
in
$T^i_C$
in
 $\mathcal{T}$
.
$\mathcal{T}$
.
-
(3′) There is a fixed integer
 $m$
such that each representable functor
$m$
such that each representable functor
 $\mathcal{C}(\,\,\,\,,C)$
has an exact sequence
with
$\mathcal{C}(\,\,\,\,,C)$
has an exact sequence
with \begin{equation*}0\to \mathcal {C}(\,\,\,\,,C)\to T^0_C\to \cdots \to T^{m}_C\to 0,\end{equation*}
\begin{equation*}0\to \mathcal {C}(\,\,\,\,,C)\to T^0_C\to \cdots \to T^{m}_C\to 0,\end{equation*}
 $T^i_C$
in
$T^i_C$
in
 $\mathcal{T}$
.
$\mathcal{T}$
.
For a general subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, we use
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, we use
![]() $\mathop{\textrm{pdim}}\nolimits \mathcal{T}$
to denote the the supremum of the set of projective dimensions of all
$\mathop{\textrm{pdim}}\nolimits \mathcal{T}$
to denote the the supremum of the set of projective dimensions of all
![]() $T$
in
$T$
in
![]() $\mathcal{T}$
. If
$\mathcal{T}$
. If
![]() $\mathcal{T}$
is generalized tilting with
$\mathcal{T}$
is generalized tilting with
![]() $\mathop{\textrm{pdim}}\nolimits \mathcal{T}\leqslant n$
satisfying condition
$\mathop{\textrm{pdim}}\nolimits \mathcal{T}\leqslant n$
satisfying condition
![]() $(3^{\prime})$
, and the integer
$(3^{\prime})$
, and the integer
![]() $m$
in condition
$m$
in condition
![]() $(3^{\prime})$
equals
$(3^{\prime})$
equals
![]() $n$
, then we say
$n$
, then we say
![]() $\mathcal{T}$
is
$\mathcal{T}$
is
![]() $n$
-tilting. It should be pointed that a tilting subcategory
$n$
-tilting. It should be pointed that a tilting subcategory
![]() $\mathcal{T}$
defined in [Reference Martínez-Villa and Ortiz-Morales20, Definition 8] is exactly 1-tilting when
$\mathcal{T}$
defined in [Reference Martínez-Villa and Ortiz-Morales20, Definition 8] is exactly 1-tilting when
![]() $\mathcal{T}$
is closed under taking direct summands.
$\mathcal{T}$
is closed under taking direct summands.
Finally, we end this section by showing that there exists a natural example of a generalized tilting subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
Example 2.4.
Let
![]() $\Lambda$
be an artin
$\Lambda$
be an artin
![]() $R$
-algebra and
$R$
-algebra and
![]() $\mathcal{C}=\mathop{\textrm{add}}\nolimits \Lambda$
. Assume that
$\mathcal{C}=\mathop{\textrm{add}}\nolimits \Lambda$
. Assume that
![]() $\mathop{\textrm{Mod}}\nolimits \Lambda$
has a classical
$\mathop{\textrm{Mod}}\nolimits \Lambda$
has a classical
![]() $n$
-tilting module
$n$
-tilting module
![]() $T$
. Then we have an
$T$
. Then we have an
![]() $n$
-tilting subcategory
$n$
-tilting subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathop{\textrm{add}}\nolimits \Lambda )$
.
$\mathop{\textrm{Mod}}\nolimits \!(\mathop{\textrm{add}}\nolimits \Lambda )$
.
Proof. Since
![]() $T$
is a classical
$T$
is a classical
![]() $n$
-tilting module, it follows from [Reference Bazzoni, Mantese and Tonolo6] that
$n$
-tilting module, it follows from [Reference Bazzoni, Mantese and Tonolo6] that
![]() $T$
satisfies the following conditions:
$T$
satisfies the following conditions:
(1) There exists a projective resolution
![]() $0\to P_n\to \cdots \to P_{1}\to P_{0}\to T\to 0$
with each
$0\to P_n\to \cdots \to P_{1}\to P_{0}\to T\to 0$
with each
![]() $P_i$
finitely generated,
$P_i$
finitely generated,
(2)
![]() ${\textrm{Ext}}_{\Lambda }^{i\geqslant 1}(T,T)=0$
,
${\textrm{Ext}}_{\Lambda }^{i\geqslant 1}(T,T)=0$
,
(3) There is an exact sequence
![]() $0\to \Lambda \to T_0\to T_1\to \cdots \to T_n\to 0$
with
$0\to \Lambda \to T_0\to T_1\to \cdots \to T_n\to 0$
with
![]() $T_i\in \mathop{\textrm{add}}\nolimits \!(T)$
.
$T_i\in \mathop{\textrm{add}}\nolimits \!(T)$
.
We set
![]() $\mathcal{T}=\{\mathcal{C}(\,\,\,\,,T^{\prime})$
$\mathcal{T}=\{\mathcal{C}(\,\,\,\,,T^{\prime})$
![]() $|$
$|$
![]() $T^{\prime}\in \mathop{\textrm{add}}\nolimits T\}$
. It is easy to verify that
$T^{\prime}\in \mathop{\textrm{add}}\nolimits T\}$
. It is easy to verify that
![]() $\mathcal{T}$
is an
$\mathcal{T}$
is an
![]() $n$
-tilting subcategory of
$n$
-tilting subcategory of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
3. Equivalences induced by a generalized tilting subcategory
Our purpose in this section is to study category equivalences induced by a generalized tilting subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. First, we observe the following key result, which is vital in proving the main theorem of this section.
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. First, we observe the following key result, which is vital in proving the main theorem of this section.
Proposition 3.1.
Assume that
![]() $\mathcal{T}$
is generalized tilting with
$\mathcal{T}$
is generalized tilting with
![]() $\mathop{\textrm{pdim}}\nolimits \mathcal{T}\leqslant n$
for some integer
$\mathop{\textrm{pdim}}\nolimits \mathcal{T}\leqslant n$
for some integer
![]() $n$
. Then the following statements are equivalent for any
$n$
. Then the following statements are equivalent for any
![]() $M$
in
$M$
in
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
-
(1)
 $M\in{\mathcal{T}^{\perp _{\infty }}}$
.
$M\in{\mathcal{T}^{\perp _{\infty }}}$
. -
(2)
 $M\in$
$M\in$
 $_{\mathcal{T}}\mathcal{X}$
.
$_{\mathcal{T}}\mathcal{X}$
. -
(3)
 $M\in \mathop{\textrm{Gen}}\nolimits _n\!(\mathcal{T})$
.
$M\in \mathop{\textrm{Gen}}\nolimits _n\!(\mathcal{T})$
.
Proof. (1)
![]() $\Rightarrow$
(2) For each representable functor
$\Rightarrow$
(2) For each representable functor
![]() $\mathcal{C}(\,\,\,\,,C)$
, since
$\mathcal{C}(\,\,\,\,,C)$
, since
![]() $\mathcal{T}$
is generalized tilting, there is an exact sequence
$\mathcal{T}$
is generalized tilting, there is an exact sequence
with
![]() $T^i_C$
in
$T^i_C$
in
![]() $\mathcal{T}$
. Note that
$\mathcal{T}$
. Note that
![]() $M\in{\mathcal{T}^{\perp _{\infty }}}$
, we have a commutative diagram
$M\in{\mathcal{T}^{\perp _{\infty }}}$
, we have a commutative diagram

where
![]() $\mathop{\textrm{Tr}}\nolimits _{T^0_C}\!(M)=\sum \{{\textrm{Im}} \psi \mid \psi \in{\textrm{Hom}}_{\mathcal{C}}(T^0_C,M)\}.$
Then it follows from Diagram (3.1) that
$\mathop{\textrm{Tr}}\nolimits _{T^0_C}\!(M)=\sum \{{\textrm{Im}} \psi \mid \psi \in{\textrm{Hom}}_{\mathcal{C}}(T^0_C,M)\}.$
Then it follows from Diagram (3.1) that
![]() $\alpha$
is epic. Since
$\alpha$
is epic. Since
![]() $\alpha$
is also monic, by Yoneda’s lemma, we have
$\alpha$
is also monic, by Yoneda’s lemma, we have
Thus
![]() $M\in \mathop{\textrm{Gen}}\nolimits _1\!(\mathcal{T})$
and there is an exact sequence
$M\in \mathop{\textrm{Gen}}\nolimits _1\!(\mathcal{T})$
and there is an exact sequence
![]() $0\to M_1 \to \coprod _{T\in \mathcal{T}}T^{(X_T)}\to M\to 0$
with
$0\to M_1 \to \coprod _{T\in \mathcal{T}}T^{(X_T)}\to M\to 0$
with
![]() $X_T={\textrm{Hom}}_{\mathcal{C}}(T,M)$
. Moreover, this exact sequence remains exact after applying the functor
$X_T={\textrm{Hom}}_{\mathcal{C}}(T,M)$
. Moreover, this exact sequence remains exact after applying the functor
![]() $\phi$
to it. Observe that
$\phi$
to it. Observe that
![]() ${\textrm{Ext}}^{i\geqslant 1}_{\mathcal{C}}(T, T^{\prime(X)})=0$
for any
${\textrm{Ext}}^{i\geqslant 1}_{\mathcal{C}}(T, T^{\prime(X)})=0$
for any
![]() $T,T^{\prime}\in \mathcal{T}$
and any set
$T,T^{\prime}\in \mathcal{T}$
and any set
![]() $X$
by [Reference Martínez-Villa and Ortiz-Morales20, Proposition 4]. So
$X$
by [Reference Martínez-Villa and Ortiz-Morales20, Proposition 4]. So
![]() $M_1\in{\mathcal{T}^{\perp _{\infty }}}$
. Now repeating the process to
$M_1\in{\mathcal{T}^{\perp _{\infty }}}$
. Now repeating the process to
![]() $M_1$
, we obtain that
$M_1$
, we obtain that
![]() $M\in$
$M\in$
![]() $_{\mathcal{T}}\mathcal{X}$
.
$_{\mathcal{T}}\mathcal{X}$
.
(2)
![]() $\Rightarrow$
(3) is obvious.
$\Rightarrow$
(3) is obvious.
(3)
![]() $\Rightarrow$
(1) The case for
$\Rightarrow$
(1) The case for
![]() $n=0$
is trivial. Now suppose that
$n=0$
is trivial. Now suppose that
![]() $n\gt 0$
, then by assumption there is an exact sequence
$n\gt 0$
, then by assumption there is an exact sequence
![]() $0\to N\to T_n\to \cdots \to T_1\to M\to 0$
with
$0\to N\to T_n\to \cdots \to T_1\to M\to 0$
with
![]() $T_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
. Because
$T_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
. Because
![]() $\mathcal{T}$
is self-orthogonal, we have
$\mathcal{T}$
is self-orthogonal, we have
![]() ${\textrm{Ext}}^i_{\mathcal{C}}(T,M)\cong{\textrm{Ext}}^{i+n}_{\mathcal{C}}(T,N)$
for any
${\textrm{Ext}}^i_{\mathcal{C}}(T,M)\cong{\textrm{Ext}}^{i+n}_{\mathcal{C}}(T,N)$
for any
![]() $T$
in
$T$
in
![]() $\mathcal{T}$
and any
$\mathcal{T}$
and any
![]() $i\geqslant 1$
by dimension shift. But the latter equals 0, since
$i\geqslant 1$
by dimension shift. But the latter equals 0, since
![]() $\mathop{\textrm{pdim}}\nolimits \mathcal{T}\leqslant n$
. Therefore,
$\mathop{\textrm{pdim}}\nolimits \mathcal{T}\leqslant n$
. Therefore,
![]() $M\in{\mathcal{T}^{\perp _{\infty }}}$
.
$M\in{\mathcal{T}^{\perp _{\infty }}}$
.
The following two results, dual to each other, will be used throughout.
Lemma 3.2.
Assume that
![]() $\mathcal{T}$
is generalized tilting and
$\mathcal{T}$
is generalized tilting and
![]() $M$
is an object in
$M$
is an object in
![]() $\mathcal{T}^{\perp _{\infty }}$
. Then
$\mathcal{T}^{\perp _{\infty }}$
. Then
![]() $\phi (M)\otimes \mathcal{T}\cong M$
and
$\phi (M)\otimes \mathcal{T}\cong M$
and
![]() $\phi (M)\in{^{\top _{\infty }}\mathcal{T}}$
.
$\phi (M)\in{^{\top _{\infty }}\mathcal{T}}$
.
Proof. Since
![]() $M\in{\mathcal{T}^{\perp _{\infty }}}$
,
$M\in{\mathcal{T}^{\perp _{\infty }}}$
,
![]() $M\in$
$M\in$
![]() $_{\mathcal{T}}\mathcal{X}$
by Proposition 3.1, in particular there is an exact sequence
$_{\mathcal{T}}\mathcal{X}$
by Proposition 3.1, in particular there is an exact sequence
with
![]() $T_i=\coprod _{T\in \mathcal{T}}T^{(X_i)}$
and each
$T_i=\coprod _{T\in \mathcal{T}}T^{(X_i)}$
and each
![]() ${\textrm{Im}} \,f_i\in{\mathcal{T}^{\perp _{\infty }}}$
. Applying the functor
${\textrm{Im}} \,f_i\in{\mathcal{T}^{\perp _{\infty }}}$
. Applying the functor
![]() $\phi$
to (3.2) yields the following exact sequence
$\phi$
to (3.2) yields the following exact sequence
Thanks to [Reference Martínez-Villa and Ortiz-Morales20, Theorem 2], the functor
![]() $\phi$
preserves direct sums. Thus, each
$\phi$
preserves direct sums. Thus, each
![]() $\phi (T_i)$
is projective in
$\phi (T_i)$
is projective in
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{T})$
. Moreover, by Lemma 2.1, we have the following commutative diagram
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{T})$
. Moreover, by Lemma 2.1, we have the following commutative diagram

Consequently, we obtain that
![]() $\phi (M)\otimes \mathcal{T}\cong M$
and
$\phi (M)\otimes \mathcal{T}\cong M$
and
![]() $\phi (M)\in{^{\top _{\infty }}\mathcal{T}}$
.
$\phi (M)\in{^{\top _{\infty }}\mathcal{T}}$
.
Analogously, dualizing the proof of the above lemma, we have the following
Lemma 3.3.
Assume that
![]() $\mathcal{T}$
is generalized tilting and
$\mathcal{T}$
is generalized tilting and
![]() $N$
is an object in
$N$
is an object in
![]() $^{\top _{\infty }}\mathcal{T}$
. Then
$^{\top _{\infty }}\mathcal{T}$
. Then
![]() $N\cong \phi (N\otimes \mathcal{T})$
and
$N\cong \phi (N\otimes \mathcal{T})$
and
![]() $N\otimes \mathcal{T}\in{\mathcal{T}^{\perp _{\infty }}}$
.
$N\otimes \mathcal{T}\in{\mathcal{T}^{\perp _{\infty }}}$
.
Proof. Consider the following projective resolution of
![]() $N$
$N$
with
![]() $P_i=\coprod _{j_i\in J_i}\mathcal{T}(\,\,\,\,,T_{j_i})$
. Since
$P_i=\coprod _{j_i\in J_i}\mathcal{T}(\,\,\,\,,T_{j_i})$
. Since
![]() $({-}\otimes \mathcal{T},\phi )$
forms an adjoint pair by Lemma 2.1, the functor
$({-}\otimes \mathcal{T},\phi )$
forms an adjoint pair by Lemma 2.1, the functor
![]() $-\otimes \mathcal{T}$
preserves direct sums and
$-\otimes \mathcal{T}$
preserves direct sums and
![]() $(\coprod _{j_i\in J_i}\mathcal{T}(\,\,\,\,,T_{j_i}))\otimes \mathcal{T} \cong \coprod _{j_i\in J_i}T_{j_i}$
. By the assumption of
$(\coprod _{j_i\in J_i}\mathcal{T}(\,\,\,\,,T_{j_i}))\otimes \mathcal{T} \cong \coprod _{j_i\in J_i}T_{j_i}$
. By the assumption of
![]() $N$
, applying the functor
$N$
, applying the functor
![]() $-\otimes \mathcal{T}$
to (3.3) yields the following exact sequence
$-\otimes \mathcal{T}$
to (3.3) yields the following exact sequence
Note that
![]() $\mathcal{T}$
is generalized tilting, we have that
$\mathcal{T}$
is generalized tilting, we have that
![]() $P_i\otimes \mathcal{T}\in{\mathcal{T}^{\perp _{\infty }}}$
for any
$P_i\otimes \mathcal{T}\in{\mathcal{T}^{\perp _{\infty }}}$
for any
![]() $i\geqslant 0$
. Moreover, we have the following commutative diagram
$i\geqslant 0$
. Moreover, we have the following commutative diagram

So we get that
![]() $N\cong \phi (N\otimes \mathcal{T})$
and
$N\cong \phi (N\otimes \mathcal{T})$
and
![]() $N\otimes \mathcal{T}\in{\mathcal{T}^{\perp _{\infty }}}$
.
$N\otimes \mathcal{T}\in{\mathcal{T}^{\perp _{\infty }}}$
.
In order to present the main theorem in this section, we need to introduce the following notions.
Theorem 3.4.
Assume that
![]() $\mathcal{T}$
is generalized tilting and
$\mathcal{T}$
is generalized tilting and
![]() $e$
is a non-negative integer. Then there are two category equivalences
$e$
is a non-negative integer. Then there are two category equivalences

Proof. We can apply Lemmas 3.2 and 3.3 to conclude that the equivalence holds for
![]() $e=0$
. Now assume that
$e=0$
. Now assume that
![]() $e\geqslant 1$
and
$e\geqslant 1$
and
![]() $M\in \mathop{\textrm{KE}}\nolimits ^{\infty }_e\!(\mathcal{T})$
. Consider an injective resolution of
$M\in \mathop{\textrm{KE}}\nolimits ^{\infty }_e\!(\mathcal{T})$
. Consider an injective resolution of
![]() $M$
$M$
Since
![]() ${\textrm{Ext}}^i_{\mathcal{C}}(\,\,\,\,,{\textrm{Im}} \,f_e)_{\mathcal{T}}\cong{\textrm{Ext}}^{i+e}_{\mathcal{C}}(\,\,\,\,,M)_{\mathcal{T}}=0$
for any
${\textrm{Ext}}^i_{\mathcal{C}}(\,\,\,\,,{\textrm{Im}} \,f_e)_{\mathcal{T}}\cong{\textrm{Ext}}^{i+e}_{\mathcal{C}}(\,\,\,\,,M)_{\mathcal{T}}=0$
for any
![]() $i\geqslant 1$
. It follows from Lemma 3.2 that
$i\geqslant 1$
. It follows from Lemma 3.2 that
![]() $\phi ({\textrm{Im}} \,f_e)\otimes \mathcal{T}\cong{\textrm{Im}} \,f_e$
and
$\phi ({\textrm{Im}} \,f_e)\otimes \mathcal{T}\cong{\textrm{Im}} \,f_e$
and
![]() $\phi ({\textrm{Im}} \,f_e)\in{^{\top _{\infty }}\mathcal{T}}$
. Applying the functor
$\phi ({\textrm{Im}} \,f_e)\in{^{\top _{\infty }}\mathcal{T}}$
. Applying the functor
![]() $\phi$
to (3.4), we get an exact sequence
$\phi$
to (3.4), we get an exact sequence
with
![]() $X\cong{\textrm{Ext}}^{1}_{\mathcal{C}}(\,\,\,\,,{\textrm{Im}} \,f_{e-1})_{\mathcal{T}}\cong{\textrm{Ext}}^{e}_{\mathcal{C}}(\,\,\,\,,M)_{\mathcal{T}}.$
Because every term except
$X\cong{\textrm{Ext}}^{1}_{\mathcal{C}}(\,\,\,\,,{\textrm{Im}} \,f_{e-1})_{\mathcal{T}}\cong{\textrm{Ext}}^{e}_{\mathcal{C}}(\,\,\,\,,M)_{\mathcal{T}}.$
Because every term except
![]() $X$
in the exact sequence belongs to
$X$
in the exact sequence belongs to
![]() $^{\top _{\infty }}\mathcal{T}$
, the
$^{\top _{\infty }}\mathcal{T}$
, the
![]() $i$
th-homology can be computed by it. Therefore, we obtain that
$i$
th-homology can be computed by it. Therefore, we obtain that
![]() $\textrm{Tor}^{\mathcal{T}}_{i}(X,\mathcal{T})=0$
for any
$\textrm{Tor}^{\mathcal{T}}_{i}(X,\mathcal{T})=0$
for any
![]() $0\leqslant i\lt \infty$
and
$0\leqslant i\lt \infty$
and
![]() $i\neq e$
,
$i\neq e$
,
![]() $\textrm{Tor}^{\mathcal{T}}_{e}(X,\mathcal{T})\cong M$
.
$\textrm{Tor}^{\mathcal{T}}_{e}(X,\mathcal{T})\cong M$
.
Conversely, suppose that
![]() $N\in \mathop{\textrm{KT}}\nolimits ^{\infty }_e\!(\mathcal{T})$
. Consider a projective resolution of
$N\in \mathop{\textrm{KT}}\nolimits ^{\infty }_e\!(\mathcal{T})$
. Consider a projective resolution of
![]() $N$
$N$
with
![]() $P_i=\coprod _{j_i\in J_i}\mathcal{T}(\,\,\,\,,T_{j_i})$
. Since
$P_i=\coprod _{j_i\in J_i}\mathcal{T}(\,\,\,\,,T_{j_i})$
. Since
![]() $\textrm{Tor}^{\mathcal{T}}_{i}({\textrm{Im}}\, g_e,\mathcal{T})\cong \textrm{Tor}^{\mathcal{T}}_{i+e}(N,\mathcal{T})=0$
for any
$\textrm{Tor}^{\mathcal{T}}_{i}({\textrm{Im}}\, g_e,\mathcal{T})\cong \textrm{Tor}^{\mathcal{T}}_{i+e}(N,\mathcal{T})=0$
for any
![]() $i\geqslant 1$
. It follows from Lemma 3.3 that
$i\geqslant 1$
. It follows from Lemma 3.3 that
![]() ${\textrm{Im}}\, g_e\cong \phi ({\textrm{Im}}\, g_e\otimes \mathcal{T})$
and
${\textrm{Im}}\, g_e\cong \phi ({\textrm{Im}}\, g_e\otimes \mathcal{T})$
and
![]() ${\textrm{Im}}\, g_e\otimes \mathcal{T}\in{\mathcal{T}^{\perp _{\infty }}}$
. Applying the functor
${\textrm{Im}}\, g_e\otimes \mathcal{T}\in{\mathcal{T}^{\perp _{\infty }}}$
. Applying the functor
![]() $-\otimes \mathcal{T}$
to (3.5), we get an exact sequence
$-\otimes \mathcal{T}$
to (3.5), we get an exact sequence
with
![]() $Y\cong \textrm{Tor}^{\mathcal{T}}_{1}({\textrm{Im}}\, g_{e-1},\mathcal{T})\cong \textrm{Tor}^{\mathcal{T}}_{e}(N,\mathcal{T})$
. Because every term except
$Y\cong \textrm{Tor}^{\mathcal{T}}_{1}({\textrm{Im}}\, g_{e-1},\mathcal{T})\cong \textrm{Tor}^{\mathcal{T}}_{e}(N,\mathcal{T})$
. Because every term except
![]() $Y$
in the exact sequence belongs to
$Y$
in the exact sequence belongs to
![]() $\mathcal{T}^{\perp _{\infty }}$
, the
$\mathcal{T}^{\perp _{\infty }}$
, the
![]() $i$
th-cohomology can be computed by it. Therefore, we obtain that
$i$
th-cohomology can be computed by it. Therefore, we obtain that
![]() ${\textrm{Ext}}_{\mathcal{C}}^{i}(\,\,\,\,,Y)_{\mathcal{T}}=0$
for any
${\textrm{Ext}}_{\mathcal{C}}^{i}(\,\,\,\,,Y)_{\mathcal{T}}=0$
for any
![]() $0\leqslant i\lt \infty$
and
$0\leqslant i\lt \infty$
and
![]() $i\neq e$
,
$i\neq e$
,
![]() ${\textrm{Ext}}_{\mathcal{C}}^{e}(\,\,\,\,,Y)_{\mathcal{T}}\cong N$
.
${\textrm{Ext}}_{\mathcal{C}}^{e}(\,\,\,\,,Y)_{\mathcal{T}}\cong N$
.
Given a 1-tilting subcategory
![]() $\mathcal{T}$
, Martínez-Villa and Ortiz-Morales in [Reference Martínez-Villa and Ortiz-Morales20, Theorem 3] proved that
$\mathcal{T}$
, Martínez-Villa and Ortiz-Morales in [Reference Martínez-Villa and Ortiz-Morales20, Theorem 3] proved that
![]() $\phi$
and
$\phi$
and
![]() $-\otimes \mathcal{T}$
induce an equivalence between
$-\otimes \mathcal{T}$
induce an equivalence between
![]() $\mathop{\textrm{KE}}\nolimits ^{1}_0(\mathcal{T})$
and
$\mathop{\textrm{KE}}\nolimits ^{1}_0(\mathcal{T})$
and
![]() $\mathop{\textrm{KT}}\nolimits ^{1}_0(\mathcal{T})$
. We generalize this result to
$\mathop{\textrm{KT}}\nolimits ^{1}_0(\mathcal{T})$
. We generalize this result to
![]() $n$
-tilting subcategory
$n$
-tilting subcategory
![]() $\mathcal{T}$
as follows.
$\mathcal{T}$
as follows.
Corollary 3.5.
Assume that
![]() $\mathcal{T}$
is
$\mathcal{T}$
is
![]() $n$
-tilting. Then for any
$n$
-tilting. Then for any
![]() $0\leqslant e\leqslant n$
, there are two category equivalences
$0\leqslant e\leqslant n$
, there are two category equivalences

Proof. Since
![]() $\mathop{\textrm{pdim}}\nolimits \!(\mathcal{T})\leqslant n$
, it is obvious that
$\mathop{\textrm{pdim}}\nolimits \!(\mathcal{T})\leqslant n$
, it is obvious that
![]() $\mathop{\textrm{KE}}\nolimits ^n_e\!(\mathcal{T})=\mathop{\textrm{KE}}\nolimits ^{\infty }_e\!(\mathcal{T})$
. For each representable functor
$\mathop{\textrm{KE}}\nolimits ^n_e\!(\mathcal{T})=\mathop{\textrm{KE}}\nolimits ^{\infty }_e\!(\mathcal{T})$
. For each representable functor
![]() $ \mathcal{C}(\,\,\,\,,C)$
, there is an exact resolution
$ \mathcal{C}(\,\,\,\,,C)$
, there is an exact resolution
with
![]() $T^i$
in
$T^i$
in
![]() $\mathcal{T}$
. Then we get a projective resolution of
$\mathcal{T}$
. Then we get a projective resolution of
![]() $(\mathcal{C}(\,\,\,\,,C),\,\,\,\,)_{\mathcal{T}}$
:
$(\mathcal{C}(\,\,\,\,,C),\,\,\,\,)_{\mathcal{T}}$
:
Then [Reference Martínez-Villa and Ortiz-Morales20, Proposition 14] implies that
![]() $\textrm{Tor}_i^{\mathcal{T}}((\mathcal{C}(\,\,\,\,,C),\,\,\,\,)_{\mathcal{T}},N)\cong \textrm{Tor}_i^{\mathcal{T}}(N,\mathcal{T})(C)=0$
for any
$\textrm{Tor}_i^{\mathcal{T}}((\mathcal{C}(\,\,\,\,,C),\,\,\,\,)_{\mathcal{T}},N)\cong \textrm{Tor}_i^{\mathcal{T}}(N,\mathcal{T})(C)=0$
for any
![]() $N\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{T})$
and
$N\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{T})$
and
![]() $i\geqslant n+1$
. So the two categories
$i\geqslant n+1$
. So the two categories
![]() $\mathop{\textrm{KT}}\nolimits ^n_e\!(\mathcal{T})$
and
$\mathop{\textrm{KT}}\nolimits ^n_e\!(\mathcal{T})$
and
![]() $\mathop{\textrm{KT}}\nolimits ^{\infty }_e\!(\mathcal{T})$
coincide. Finally, the conclusion follows by Theorem 3.4.
$\mathop{\textrm{KT}}\nolimits ^{\infty }_e\!(\mathcal{T})$
coincide. Finally, the conclusion follows by Theorem 3.4.
According to [Reference Martínez-Villa and Ortiz-Morales21], we say
![]() $\mathcal{C}$
has pseudokernels if given a map
$\mathcal{C}$
has pseudokernels if given a map
![]() $f\,:\,C_1\to C_0$
in
$f\,:\,C_1\to C_0$
in
![]() $\mathcal{C}$
, there is a map
$\mathcal{C}$
, there is a map
![]() $g\,:\,C_2\to C_1$
in
$g\,:\,C_2\to C_1$
in
![]() $\mathcal{C}$
such that the sequence of representable functors
$\mathcal{C}$
such that the sequence of representable functors
![]() $\mathcal{C}(\,\,\,\,, C_2)\stackrel{\mathcal{C}(\,\,\,\,, g)}{\longrightarrow } \mathcal{C}(\,\,\,\,, C_1)\stackrel{\mathcal{C}(\,\,\,\,, f)}{\longrightarrow }\mathcal{C}(\,\,\,\,, C_0)$
is exact. Since
$\mathcal{C}(\,\,\,\,, C_2)\stackrel{\mathcal{C}(\,\,\,\,, g)}{\longrightarrow } \mathcal{C}(\,\,\,\,, C_1)\stackrel{\mathcal{C}(\,\,\,\,, f)}{\longrightarrow }\mathcal{C}(\,\,\,\,, C_0)$
is exact. Since
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
is an abelian category,
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
is an abelian category,
![]() $\mathcal{C}$
has pseudokernels if and only if
$\mathcal{C}$
has pseudokernels if and only if
![]() $\mathop{\textrm{Ker}}\nolimits \!(, f)$
is finitely generated for each
$\mathop{\textrm{Ker}}\nolimits \!(, f)$
is finitely generated for each
![]() $f\,:\,C_1\to C_0$
in
$f\,:\,C_1\to C_0$
in
![]() $\mathcal{C}$
. Next we turn to investigating the invariance of Grothendieck groups under generalized tilting. To this end, we need the following.
$\mathcal{C}$
. Next we turn to investigating the invariance of Grothendieck groups under generalized tilting. To this end, we need the following.
Definition 3.6. ([Reference Martínez-Villa and Ortiz-Morales20, Definition 10]) Let
![]() $\mathcal{C}$
be a skeletally small preadditive category with pseudokernels. Let’s define by
$\mathcal{C}$
be a skeletally small preadditive category with pseudokernels. Let’s define by
![]() $|\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})|$
the set of isomorphism classes of objects in
$|\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})|$
the set of isomorphism classes of objects in
![]() $|\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})|$
. Let
$|\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})|$
. Let
![]() $\mathcal{A}$
be the free abelian group generated by
$\mathcal{A}$
be the free abelian group generated by
![]() $|\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})|$
and
$|\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})|$
and
![]() $\mathcal{R}$
the subgroup of
$\mathcal{R}$
the subgroup of
![]() $\mathcal{A}$
generated by relations
$\mathcal{A}$
generated by relations
![]() $[M]-[K]-[L]$
where
$[M]-[K]-[L]$
where
![]() $0\to K\to M\to L\to 0$
is a short exact sequence in
$0\to K\to M\to L\to 0$
is a short exact sequence in
![]() $\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
. Then, the Grothendieck group of
$\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
. Then, the Grothendieck group of
![]() $\mathcal{C}$
is
$\mathcal{C}$
is
![]() $\mathcal{K}_0(\mathcal{C})=\mathcal{A}/\mathcal{R}$
.
$\mathcal{K}_0(\mathcal{C})=\mathcal{A}/\mathcal{R}$
.
It was proved in [Reference Auslander and Reiten4] that
![]() $\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
is abelian if and only if
$\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
is abelian if and only if
![]() $\mathcal{C}$
has pseudokernels. We will use this result to show the following proposition.
$\mathcal{C}$
has pseudokernels. We will use this result to show the following proposition.
Proposition 3.7.
Let
![]() $\mathcal{C}$
be an annuli variety and
$\mathcal{C}$
be an annuli variety and
![]() $\mathcal{T}$
a generalized tilting subcategory of
$\mathcal{T}$
a generalized tilting subcategory of
![]() $\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
. Assume
$\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
. Assume
![]() $\mathcal{C}$
and
$\mathcal{C}$
and
![]() $\mathcal{T}$
have pseudokernels. Then the following statements hold.
$\mathcal{T}$
have pseudokernels. Then the following statements hold.
-
(1)
 ${\textrm{Ext}}^i_{\mathcal{C}}(\,\,\,\,,M)_{\mathcal{T}}\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
for any
${\textrm{Ext}}^i_{\mathcal{C}}(\,\,\,\,,M)_{\mathcal{T}}\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
for any
 $M\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
and any
$M\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
and any
 $i\geqslant 0$
.
$i\geqslant 0$
. -
(2)
 $\textrm{Tor}_i^{\mathcal{T}}(N,\mathcal{T})\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
for any
$\textrm{Tor}_i^{\mathcal{T}}(N,\mathcal{T})\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
for any
 $N\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
and any
$N\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
and any
 $i\geqslant 0$
.
$i\geqslant 0$
.
Proof. (1) Since
![]() $\mathcal{T}$
is generalized tilting, we may assume that
$\mathcal{T}$
is generalized tilting, we may assume that
![]() $\mathop{\textrm{pdim}}\nolimits \mathcal{T}\leqslant n$
for some integer
$\mathop{\textrm{pdim}}\nolimits \mathcal{T}\leqslant n$
for some integer
![]() $n$
. Let
$n$
. Let
![]() $M \in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
, then there is an exact sequence
$M \in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
, then there is an exact sequence
![]() $0\to K_1\to \mathcal{C}(\,\,\,\,,C_0)\to M\to 0$
with
$0\to K_1\to \mathcal{C}(\,\,\,\,,C_0)\to M\to 0$
with
![]() $K_1 \in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
. Applying the functor
$K_1 \in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
. Applying the functor
![]() $\phi$
to this exact sequence gives rise to the following exact sequence
$\phi$
to this exact sequence gives rise to the following exact sequence
It follows from the proof of [Reference Martínez-Villa and Ortiz-Morales21, Proposition 6] that
![]() ${\textrm{Ext}}^i_{\mathcal{C}}(\,\,\,\,,K_1)_{\mathcal{T}}$
is in
${\textrm{Ext}}^i_{\mathcal{C}}(\,\,\,\,,K_1)_{\mathcal{T}}$
is in
![]() $\mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
for any
$\mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
for any
![]() $i \geqslant 0$
. On the other hand, by [Reference Martínez-Villa and Ortiz-Morales21, Lemma 5], we know that
$i \geqslant 0$
. On the other hand, by [Reference Martínez-Villa and Ortiz-Morales21, Lemma 5], we know that
![]() ${\textrm{Ext}}^i_{\mathcal{C}}(\,\,\,\,,\mathcal{C}(\,\,\,\,,C_0))_{\mathcal{T}}$
is also in
${\textrm{Ext}}^i_{\mathcal{C}}(\,\,\,\,,\mathcal{C}(\,\,\,\,,C_0))_{\mathcal{T}}$
is also in
![]() $\mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
for any
$\mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
for any
![]() $i \geqslant 0$
. So
$i \geqslant 0$
. So
![]() ${\textrm{Ext}}^i_{\mathcal{C}}(\,\,\,\,,M)_{\mathcal{T}}\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
for any
${\textrm{Ext}}^i_{\mathcal{C}}(\,\,\,\,,M)_{\mathcal{T}}\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
for any
![]() $i\geqslant 0$
since
$i\geqslant 0$
since
![]() $\mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
is abelian.
$\mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
is abelian.
(2) Let
![]() $N\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
and
$N\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
and
a projective resolution of
![]() $N$
. Set
$N$
. Set
![]() $L_i={\textrm{Im}} \,f_i$
and split the resolution in short exact sequences:
$L_i={\textrm{Im}} \,f_i$
and split the resolution in short exact sequences:
![]() $0\to L_{i+1} \to \mathcal{T}(\,\,\,\,,T_i)\to L_i\to 0$
. Thus it follows from the long homology sequence that there are exact sequences:
$0\to L_{i+1} \to \mathcal{T}(\,\,\,\,,T_i)\to L_i\to 0$
. Thus it follows from the long homology sequence that there are exact sequences:
Since
![]() $T_1\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
,
$T_1\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
,
![]() $L_1\otimes \mathcal{T}$
is finitely generated. Thus,
$L_1\otimes \mathcal{T}$
is finitely generated. Thus,
![]() ${\textrm{Im}} (L_1\otimes \mathcal{T}\to T_0)$
is finitely generated and so
${\textrm{Im}} (L_1\otimes \mathcal{T}\to T_0)$
is finitely generated and so
![]() $N\otimes \mathcal{T}$
is finitely presented. Similarly, as
$N\otimes \mathcal{T}$
is finitely presented. Similarly, as
![]() $L_1\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
,
$L_1\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
,
![]() $L_1\otimes \mathcal{T}$
is finitely presented. Note that
$L_1\otimes \mathcal{T}$
is finitely presented. Note that
![]() $\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
is abelian. We get that
$\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
is abelian. We get that
![]() $\textrm{Tor}_1^{\mathcal{T}}(N,\mathcal{T})$
is finitely presented. Because
$\textrm{Tor}_1^{\mathcal{T}}(N,\mathcal{T})$
is finitely presented. Because
![]() $\textrm{Tor}_i^{\mathcal{T}}(N,\mathcal{T})\cong \textrm{Tor}_1^{\mathcal{T}}(L_{i-1},\mathcal{T})$
for any
$\textrm{Tor}_i^{\mathcal{T}}(N,\mathcal{T})\cong \textrm{Tor}_1^{\mathcal{T}}(L_{i-1},\mathcal{T})$
for any
![]() $i\geqslant 2$
,
$i\geqslant 2$
,
![]() $\textrm{Tor}_i^{\mathcal{T}}(N,\mathcal{T})\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
.
$\textrm{Tor}_i^{\mathcal{T}}(N,\mathcal{T})\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
.
We now come to the first application in this section, our method in the following has its origin in [Reference Miyashita26, Theorem 1.19].
Theorem 3.8.
Let
![]() $\mathcal{C}$
be an abelian category with enough injectives and
$\mathcal{C}$
be an abelian category with enough injectives and
![]() $\mathcal{T}$
an
$\mathcal{T}$
an
![]() $n$
-tilting subcategory of
$n$
-tilting subcategory of
![]() $\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
with pseudokernels. Then the Grothendieck groups
$\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
with pseudokernels. Then the Grothendieck groups
![]() $K_0(\mathcal{C})$
and
$K_0(\mathcal{C})$
and
![]() $K_0(\mathcal{T})$
are isomorphic.
$K_0(\mathcal{T})$
are isomorphic.
Proof. We define two group homomorphisms
It is easily seen by Proposition 3.7 that
![]() $F$
and
$F$
and
![]() $G$
are well defined. For any
$G$
are well defined. For any
![]() $M\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
, since
$M\in \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
, since
![]() $\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
has enough injectives by [Reference Russell29, Section 6], we have an injective resolution
$\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
has enough injectives by [Reference Russell29, Section 6], we have an injective resolution
in
![]() $\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
. Set
$\mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
. Set
![]() $K_i={\textrm{Im}} \,f_i$
. Then
$K_i={\textrm{Im}} \,f_i$
. Then
![]() $K_n\in \mathop{\textrm{KE}}\nolimits ^{\infty }_0\!(\mathcal{T})\bigcap \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
. Thus,
$K_n\in \mathop{\textrm{KE}}\nolimits ^{\infty }_0\!(\mathcal{T})\bigcap \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
. Thus,
![]() $K_0(\mathcal{C})$
is generated by the set of all
$K_0(\mathcal{C})$
is generated by the set of all
![]() $[X]$
with
$[X]$
with
![]() $X\in \mathop{\textrm{KE}}\nolimits ^{\infty }_0(\mathcal{T})\bigcap \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
. Dually we have that
$X\in \mathop{\textrm{KE}}\nolimits ^{\infty }_0(\mathcal{T})\bigcap \mathop{\textrm{mod}}\nolimits \!(\mathcal{C})$
. Dually we have that
![]() $K_0(\mathcal{T})$
is generated by the set of all
$K_0(\mathcal{T})$
is generated by the set of all
![]() $[Y]$
with
$[Y]$
with
![]() $Y\in \mathop{\textrm{KT}}\nolimits ^{\infty }_0(\mathcal{T})\bigcap \mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
. Since
$Y\in \mathop{\textrm{KT}}\nolimits ^{\infty }_0(\mathcal{T})\bigcap \mathop{\textrm{mod}}\nolimits \!(\mathcal{T})$
. Since
![]() $GF([X])=[X]$
and
$GF([X])=[X]$
and
![]() $FG([Y])=[Y]$
by Theorem 3.4, we conclude that
$FG([Y])=[Y]$
by Theorem 3.4, we conclude that
![]() $K_0(\mathcal{C})$
and
$K_0(\mathcal{C})$
and
![]() $K_0(\mathcal{T})$
are isomorphic.
$K_0(\mathcal{T})$
are isomorphic.
Given
![]() $M\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, since
$M\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, since
![]() $M$
has an injective envelope by [Reference Jensen and Lenzing19, Theorem B.3], we have a minimal injective resolution
$M$
has an injective envelope by [Reference Jensen and Lenzing19, Theorem B.3], we have a minimal injective resolution
![]() $0\rightarrow M \rightarrow I_0 \stackrel{f_0}{\longrightarrow } I_1\stackrel{f_1}{\longrightarrow }\cdots .$
Then
$0\rightarrow M \rightarrow I_0 \stackrel{f_0}{\longrightarrow } I_1\stackrel{f_1}{\longrightarrow }\cdots .$
Then
![]() $\mathop{\textrm{cTr}}\nolimits _{\mathcal{T}} M\,:\!=\,\mathop{\textrm{Coker}}\nolimits \phi ({f_0})$
is called the cotranspose of
$\mathop{\textrm{cTr}}\nolimits _{\mathcal{T}} M\,:\!=\,\mathop{\textrm{Coker}}\nolimits \phi ({f_0})$
is called the cotranspose of
![]() $M$
with respect to
$M$
with respect to
![]() $\mathcal{T}$
. The notion is analogous to the cotranspose of a module with respect to a semidualizing bimodule defined in [Reference Tang and Huang32, Defintion 3.1]. Using the tool of cotransposes, Tang and Huang in [Reference Tang and Huang32, Proposition 3.2] established the so-called dual Auslander sequence. We will apply Theorem 3.4 to conclude that the dual Auslander sequence still holds in functor categories, but the approach used here is different.
$\mathcal{T}$
. The notion is analogous to the cotranspose of a module with respect to a semidualizing bimodule defined in [Reference Tang and Huang32, Defintion 3.1]. Using the tool of cotransposes, Tang and Huang in [Reference Tang and Huang32, Proposition 3.2] established the so-called dual Auslander sequence. We will apply Theorem 3.4 to conclude that the dual Auslander sequence still holds in functor categories, but the approach used here is different.
Corollary 3.9.
Assume that
![]() $\mathcal{T}$
is generalized tilting. Then for any
$\mathcal{T}$
is generalized tilting. Then for any
![]() $M\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, there is an exact sequence
$M\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, there is an exact sequence
Proof. Let
![]() $0\to M\to I_0\to I_1\to \cdots$
be a minimal injective resolution of
$0\to M\to I_0\to I_1\to \cdots$
be a minimal injective resolution of
![]() $M$
. Applying the functor
$M$
. Applying the functor
![]() $\phi$
to it yields an exact sequence
$\phi$
to it yields an exact sequence

where
![]() $K={\textrm{Im}}(\phi (I_0)\to \phi (I_1)).$
By Theorem 3.4, now applying the functor
$K={\textrm{Im}}(\phi (I_0)\to \phi (I_1)).$
By Theorem 3.4, now applying the functor
![]() $\otimes \mathcal{T}$
to Diagram (3.6) gives rise to the following diagram
$\otimes \mathcal{T}$
to Diagram (3.6) gives rise to the following diagram

Therefore the left most column in the above diagram is as desired.
4. Cotorsion pair and model category structure
Our goal in this section is to construct a cotorsion pair induced by a generalized tilting subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, allowing us to provide a model category structure on the category of complexes
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, allowing us to provide a model category structure on the category of complexes
![]() $\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
. For the definition of a model structure, we refer to the book by Hoevy [Reference Hovey18].
$\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
. For the definition of a model structure, we refer to the book by Hoevy [Reference Hovey18].
The following lemma is straightforward, but we include a proof as we have not been able to find a suitable reference for it.
Lemma 4.1.
Suppose that
![]() $\mathcal{T}$
is a subcategory of
$\mathcal{T}$
is a subcategory of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. Then the following statements hold.
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. Then the following statements hold.
-
(1) If
 $\mathcal{T}$
is closed under cokernels of monomorphisms and contains all injective objects in
$\mathcal{T}$
is closed under cokernels of monomorphisms and contains all injective objects in
 $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, then
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, then
 ${^{\perp _{\infty }}\mathcal{T}}={^{\perp _{1}}\mathcal{T}}$
.
${^{\perp _{\infty }}\mathcal{T}}={^{\perp _{1}}\mathcal{T}}$
. -
(2) If
 $\mathcal{T}$
is closed under kernels of epimorphisms and contains all projective objects in
$\mathcal{T}$
is closed under kernels of epimorphisms and contains all projective objects in
 $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, then
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, then
 $\mathcal{T}^{\perp _{\infty }}=\mathcal{T}^{\perp _{1}}$
.
$\mathcal{T}^{\perp _{\infty }}=\mathcal{T}^{\perp _{1}}$
.
Proof. We show the first statement of the lemma. The second statement follows from a dual argument.
(1) It is enough to show that
![]() ${^{\perp _{1}}\mathcal{T}} \subseteq{^{\perp _{\infty }}\mathcal{T}}$
. Let
${^{\perp _{1}}\mathcal{T}} \subseteq{^{\perp _{\infty }}\mathcal{T}}$
. Let
![]() $X\in{^{\perp _{1}}\mathcal{T}}$
and
$X\in{^{\perp _{1}}\mathcal{T}}$
and
![]() $M\in \mathcal{T}$
, then we have an exact sequence
$M\in \mathcal{T}$
, then we have an exact sequence
![]() $0\to M\to I_0\to I_1\to \cdots \to I_i \to \cdots$
with
$0\to M\to I_0\to I_1\to \cdots \to I_i \to \cdots$
with
![]() $I_i$
injective. Set
$I_i$
injective. Set
![]() $K_i=\mathop{\textrm{Ker}}\nolimits \!(I_i\to I_{i+1})$
. By assumption, both
$K_i=\mathop{\textrm{Ker}}\nolimits \!(I_i\to I_{i+1})$
. By assumption, both
![]() $I_i$
and
$I_i$
and
![]() $K_i$
are in
$K_i$
are in
![]() $\mathcal{T}$
. So
$\mathcal{T}$
. So
![]() ${\textrm{Ext}}^i_{\mathcal{C}}(X,M)\cong{\textrm{Ext}}^1_{\mathcal{C}}(X,K_{i-1})=0$
for any
${\textrm{Ext}}^i_{\mathcal{C}}(X,M)\cong{\textrm{Ext}}^1_{\mathcal{C}}(X,K_{i-1})=0$
for any
![]() $i\gt 1$
.
$i\gt 1$
.
Now we consider the relation between
![]() $\mathop{\textrm{Gen}}\nolimits _n\!(\mathcal{T})$
and
$\mathop{\textrm{Gen}}\nolimits _n\!(\mathcal{T})$
and
![]() $\mathop{\textrm{Gen}}\nolimits _n\!(_{\mathcal{T}}\mathcal{X})$
.
$\mathop{\textrm{Gen}}\nolimits _n\!(_{\mathcal{T}}\mathcal{X})$
.
Lemma 4.2.
Assume that
![]() $\mathcal{T}$
is a subcategory of
$\mathcal{T}$
is a subcategory of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. If there is an exact sequence
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. If there is an exact sequence
![]() $0\to L\to K_n\to \cdots \to K_1\to M\to 0$
in
$0\to L\to K_n\to \cdots \to K_1\to M\to 0$
in
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
with
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
with
![]() $K_i\in$
$K_i\in$
![]() $_{\mathcal{T}}\mathcal{X}$
, then there is an exact sequence
$_{\mathcal{T}}\mathcal{X}$
, then there is an exact sequence
![]() $0\to U_n\to V_n\to L\to 0$
for some
$0\to U_n\to V_n\to L\to 0$
for some
![]() $U_n\in$
$U_n\in$
![]() $_{\mathcal{T}}\mathcal{X}$
, and some
$_{\mathcal{T}}\mathcal{X}$
, and some
![]() $V_n$
such that there is an exact sequence
$V_n$
such that there is an exact sequence
![]() $0\to V_n\to T_n\to \cdots \to T_1\to M\to 0$
with
$0\to V_n\to T_n\to \cdots \to T_1\to M\to 0$
with
![]() $T_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
.
$T_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
.
Proof. The proof is modeled on [Reference Wei33, Lemma 3.5(1)]. We shall prove the statement by induction on
![]() $n$
. When
$n$
. When
![]() $n=1$
, we have an exact sequence
$n=1$
, we have an exact sequence
![]() $0\to L\to K_1\to M\to 0$
with
$0\to L\to K_1\to M\to 0$
with
![]() $K_1\in$
$K_1\in$
![]() $_{\mathcal{T}}\mathcal{X}$
. Thus, we have another exact sequence
$_{\mathcal{T}}\mathcal{X}$
. Thus, we have another exact sequence
![]() $0\to U_1\to T_1\to K_1\to 0$
with
$0\to U_1\to T_1\to K_1\to 0$
with
![]() $T_1\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
and
$T_1\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
and
![]() $U_1\in$
$U_1\in$
![]() $_{\mathcal{T}}\mathcal{X}$
. Consider the following pull-back diagram
$_{\mathcal{T}}\mathcal{X}$
. Consider the following pull-back diagram

Then the middle row and left column in Diagram (4.1) are the desired exact sequences. Now assume that the conclusion is true for
![]() $n-1$
. We will show that the conclusion holds for
$n-1$
. We will show that the conclusion holds for
![]() $n$
. Set
$n$
. Set
![]() $L^{\prime}=\mathop{\textrm{Coker}}\nolimits \!(L\to K_n)$
. Then, by the induction assumption, there is an exact sequence
$L^{\prime}=\mathop{\textrm{Coker}}\nolimits \!(L\to K_n)$
. Then, by the induction assumption, there is an exact sequence
![]() $0\to U_{n-1}\to V_{n-1}\to L^{\prime}\to 0$
for some
$0\to U_{n-1}\to V_{n-1}\to L^{\prime}\to 0$
for some
![]() $U_{n-1}\in$
$U_{n-1}\in$
![]() $_{\mathcal{T}}\mathcal{X}$
, and some
$_{\mathcal{T}}\mathcal{X}$
, and some
![]() $V_{n-1}$
such that there is an exact sequence
$V_{n-1}$
such that there is an exact sequence
![]() $0\to V_{n-1}\to T_{n-1}\to \cdots \to T_1\to M\to 0$
with
$0\to V_{n-1}\to T_{n-1}\to \cdots \to T_1\to M\to 0$
with
![]() $T_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
. Then we can construct the following pullback diagram
$T_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
. Then we can construct the following pullback diagram

Since
![]() $U_{n-1}, K_n\in$
$U_{n-1}, K_n\in$
![]() $_{\mathcal{T}}\mathcal{X}$
and
$_{\mathcal{T}}\mathcal{X}$
and
![]() $_{\mathcal{T}}\mathcal{X}$
is closed under extensions by [Reference Enochs and Jenda11, Lemma 8.2.1], we get that
$_{\mathcal{T}}\mathcal{X}$
is closed under extensions by [Reference Enochs and Jenda11, Lemma 8.2.1], we get that
![]() $X\in$
$X\in$
![]() $_{\mathcal{T}}\mathcal{X}$
. Thus, there is an exact sequence
$_{\mathcal{T}}\mathcal{X}$
. Thus, there is an exact sequence
![]() $0\to U_n\to T_n\to X\to 0$
with
$0\to U_n\to T_n\to X\to 0$
with
![]() $T_n \in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
and
$T_n \in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
and
![]() $U_n\in$
$U_n\in$
![]() $_{\mathcal{T}}\mathcal{X}$
. Consider the following pull-back diagram
$_{\mathcal{T}}\mathcal{X}$
. Consider the following pull-back diagram

Now the left column in Diagram (4.3) is the desired exact sequence.
Our main aim in this section is to show that the following holds.
Theorem 4.3.
Suppose that
![]() $\mathcal{T}$
is a generalized tilting subcategory of
$\mathcal{T}$
is a generalized tilting subcategory of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
with
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
with
![]() $\mathop{\textrm{pdim}}\nolimits \!(\mathcal{T})\leqslant n$
. Then the following statements hold.
$\mathop{\textrm{pdim}}\nolimits \!(\mathcal{T})\leqslant n$
. Then the following statements hold.
-
(1)
 $(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}),\mathcal{T}^{\perp _{\infty }})$
is a hereditary and complete cotorsion pair.
$(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}),\mathcal{T}^{\perp _{\infty }})$
is a hereditary and complete cotorsion pair.
-
(2)
 $\mathop{\textrm{pdim}}\nolimits \!(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}))\leqslant n$
.
$\mathop{\textrm{pdim}}\nolimits \!(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}))\leqslant n$
. -
(3)
 $^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})\cap \mathcal{T}^{\perp _{\infty }}=\mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
.
$^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})\cap \mathcal{T}^{\perp _{\infty }}=\mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
.
Proof. (1) Since
![]() $\mathcal{T}^{\perp _{\infty }}$
is closed under cokernels of monomorphisms and contains all injective objects, it follows from Lemma 4.1(1) that
$\mathcal{T}^{\perp _{\infty }}$
is closed under cokernels of monomorphisms and contains all injective objects, it follows from Lemma 4.1(1) that
![]() $^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})=^{\perp _{1}}$
$^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})=^{\perp _{1}}$
![]() $({\mathcal{T}^{\perp _{\infty }}})$
. On the other hand, since
$({\mathcal{T}^{\perp _{\infty }}})$
. On the other hand, since
![]() $^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})$
is closed under kernels of epimorphisms and contains all projective objects, we have
$^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})$
is closed under kernels of epimorphisms and contains all projective objects, we have
![]() $(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}))^{\perp _1}=(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}))^{\perp _{\infty }}$
Lemma 4.1(2). Thus,
$(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}))^{\perp _1}=(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}))^{\perp _{\infty }}$
Lemma 4.1(2). Thus,
![]() $(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}))^{\perp _1}=\mathcal{T}^{\perp _{\infty }}$
. Hence,
$(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}))^{\perp _1}=\mathcal{T}^{\perp _{\infty }}$
. Hence,
![]() $(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}),\mathcal{T}^{\perp _{\infty }})$
forms a hereditary cotorsion pair. For each
$(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}),\mathcal{T}^{\perp _{\infty }})$
forms a hereditary cotorsion pair. For each
![]() $T\in \mathcal{T}$
, by assumption, there is a projective resolution
$T\in \mathcal{T}$
, by assumption, there is a projective resolution
![]() $0\to P_n(T)\to \cdots \to P_1(T)\to P_0(T)\to T\to 0$
. Set
$0\to P_n(T)\to \cdots \to P_1(T)\to P_0(T)\to T\to 0$
. Set
![]() $K_i(T)={\textrm{Im}} (P_{i}(T)\to P_{i-1}(T))$
for
$K_i(T)={\textrm{Im}} (P_{i}(T)\to P_{i-1}(T))$
for
![]() $1\leqslant i\leqslant n$
and
$1\leqslant i\leqslant n$
and
![]() $\mathcal{X}=\{K_i(T)\mid T\in \mathcal{T}\}\cup \mathcal{T}$
. Obviously,
$\mathcal{X}=\{K_i(T)\mid T\in \mathcal{T}\}\cup \mathcal{T}$
. Obviously,
![]() $\mathcal{X}$
is a set and
$\mathcal{X}$
is a set and
![]() $\mathcal{X}^{\perp _1}=\mathcal{T}^{\perp _{\infty }}$
. It implies that
$\mathcal{X}^{\perp _1}=\mathcal{T}^{\perp _{\infty }}$
. It implies that
![]() $(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}),\mathcal{T}^{\perp _{\infty }})$
is generated by a set
$(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}),\mathcal{T}^{\perp _{\infty }})$
is generated by a set
![]() $\mathcal{X}$
. We conclude by [Reference Holm and Jørgensen16] that
$\mathcal{X}$
. We conclude by [Reference Holm and Jørgensen16] that
![]() $(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}),\mathcal{T}^{\perp _{\infty }})$
is a complete cotorsion pair.
$(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}),\mathcal{T}^{\perp _{\infty }})$
is a complete cotorsion pair.
(2) Let
![]() $M\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, there is an exact sequence
$M\in \mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
, there is an exact sequence
![]() $0\to M\to I_0\to I_1\to \cdots \to I_{n-1}\to K\to 0$
with
$0\to M\to I_0\to I_1\to \cdots \to I_{n-1}\to K\to 0$
with
![]() $I_i$
injective. Then
$I_i$
injective. Then
![]() $I_i\in$
$I_i\in$
![]() $_{\mathcal{T}}\mathcal{X}$
by Proposition 3.1. Thus,
$_{\mathcal{T}}\mathcal{X}$
by Proposition 3.1. Thus,
![]() $K\in \mathop{\textrm{Gen}}\nolimits _n\!(\mathcal{T})$
by Lemma 4.2. It follows from Proposition 3.1 again that
$K\in \mathop{\textrm{Gen}}\nolimits _n\!(\mathcal{T})$
by Lemma 4.2. It follows from Proposition 3.1 again that
![]() $K\in \mathcal{T}^{\perp _{\infty }}$
. Given
$K\in \mathcal{T}^{\perp _{\infty }}$
. Given
![]() $X\in$
$X\in$
![]() $^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})$
, we know that
$^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})$
, we know that
![]() ${\textrm{Ext}}^{i+n}_{\mathcal{C}}(X,M)\cong{\textrm{Ext}}^{i}_{\mathcal{C}}(X,K)=0$
for any
${\textrm{Ext}}^{i+n}_{\mathcal{C}}(X,M)\cong{\textrm{Ext}}^{i}_{\mathcal{C}}(X,K)=0$
for any
![]() $i\geqslant 1$
. Therefore, the result holds.
$i\geqslant 1$
. Therefore, the result holds.
(3)
![]() $\mathop{\textrm{Add}}\nolimits \!(\mathcal{T})\subseteq$
$\mathop{\textrm{Add}}\nolimits \!(\mathcal{T})\subseteq$
![]() $^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})\cap \mathcal{T}^{\perp _{\infty }}$
is trivial. Conversely, let
$^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})\cap \mathcal{T}^{\perp _{\infty }}$
is trivial. Conversely, let
![]() $M\in$
$M\in$
![]() $ ^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})\cap \mathcal{T}^{\perp _{\infty }}$
, then there is an exact sequence
$ ^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})\cap \mathcal{T}^{\perp _{\infty }}$
, then there is an exact sequence
![]() $0\to K\to T\to M\to 0$
with
$0\to K\to T\to M\to 0$
with
![]() $T\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
and
$T\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
and
![]() $K\in \mathcal{T}^{\perp _{\infty }}$
by Proposition 3.1. So the sequence splits, which implies that
$K\in \mathcal{T}^{\perp _{\infty }}$
by Proposition 3.1. So the sequence splits, which implies that
![]() $M\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
.
$M\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
.
Let
![]() $\mathcal{A}$
be an abelian category. A complex
$\mathcal{A}$
be an abelian category. A complex
![]() $A=(A_n, d_n^A)$
is a sequence
$A=(A_n, d_n^A)$
is a sequence
![]() $\cdots \to A_{n+1}\stackrel{d_{n+1}^A}{\longrightarrow } A_n\stackrel{d_{n}^A}{\longrightarrow } A_{n-1}\to \cdots$
with
$\cdots \to A_{n+1}\stackrel{d_{n+1}^A}{\longrightarrow } A_n\stackrel{d_{n}^A}{\longrightarrow } A_{n-1}\to \cdots$
with
![]() $A_n\in \mathcal{A}$
and
$A_n\in \mathcal{A}$
and
![]() $d_n\in{\textrm{Hom}}_{\mathcal{A}}(A_n,A_{n-1})$
satisfying
$d_n\in{\textrm{Hom}}_{\mathcal{A}}(A_n,A_{n-1})$
satisfying
![]() $d_n^A d_{n+1}^A=0$
for any
$d_n^A d_{n+1}^A=0$
for any
![]() $n\in$
$n\in$
![]() $\mathbb{Z}$
. We denote by
$\mathbb{Z}$
. We denote by
![]() $\mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
the category of complexes. A morphism
$\mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
the category of complexes. A morphism
![]() $f\,:\,X\to Y$
is said to be a quasi-isomorphism if the induced morphism
$f\,:\,X\to Y$
is said to be a quasi-isomorphism if the induced morphism
![]() $\mathop{\textrm{H}}\nolimits \!(f)\,:\, \mathop{\textrm{H}}\nolimits \!(X)\to \mathop{\textrm{H}}\nolimits \!(Y)$
is an isomorphism. Given a complex
$\mathop{\textrm{H}}\nolimits \!(f)\,:\, \mathop{\textrm{H}}\nolimits \!(X)\to \mathop{\textrm{H}}\nolimits \!(Y)$
is an isomorphism. Given a complex
![]() $A=(A_n, d_n^A)$
, the suspension of
$A=(A_n, d_n^A)$
, the suspension of
![]() $A$
, denoted
$A$
, denoted
![]() $\Sigma A$
, is the complex given by
$\Sigma A$
, is the complex given by
![]() $(\Sigma A)_n=A_{n-1}$
and
$(\Sigma A)_n=A_{n-1}$
and
![]() $d^{\Sigma A}_n=-d_{n-1}^A$
. For complexes
$d^{\Sigma A}_n=-d_{n-1}^A$
. For complexes
![]() $X$
and
$X$
and
![]() $Y$
, we define the homomorphism complex
$Y$
, we define the homomorphism complex
![]() ${\textrm{Hom}}(X,Y)\in \mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
to be the complex
${\textrm{Hom}}(X,Y)\in \mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
to be the complex
where
![]() $(\delta _nf)=d_{k+n}^Yf_k-({-}1)^nf_{k-1}d_k^X$
. We let
$(\delta _nf)=d_{k+n}^Yf_k-({-}1)^nf_{k-1}d_k^X$
. We let
![]() ${\textrm{Ext}}_{\mathop{\textrm{C}}\nolimits \!(\mathcal{A})}^1(Y,X)$
to be the group of (equivalence classes) of short exact sequences
${\textrm{Ext}}_{\mathop{\textrm{C}}\nolimits \!(\mathcal{A})}^1(Y,X)$
to be the group of (equivalence classes) of short exact sequences
![]() $0\to X\to Z\to Y\to 0$
in
$0\to X\to Z\to Y\to 0$
in
![]() $\mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
. Recall that a morphism
$\mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
. Recall that a morphism
![]() $f\,:\, X\to Y$
of complexes is called null-homotopic if there exists
$f\,:\, X\to Y$
of complexes is called null-homotopic if there exists
![]() $s_n\in{\textrm{Hom}}_{\mathcal{A}}(X_{n-1},Y_n)$
such that
$s_n\in{\textrm{Hom}}_{\mathcal{A}}(X_{n-1},Y_n)$
such that
![]() $f_n=d^Y_{n+1}s_{n+1}+s_nd^X_n$
for each
$f_n=d^Y_{n+1}s_{n+1}+s_nd^X_n$
for each
![]() $n\in$
$n\in$
![]() $\mathbb{Z}$
. For morphisms
$\mathbb{Z}$
. For morphisms
![]() $f,g\,:\, X\to Y$
in
$f,g\,:\, X\to Y$
in
![]() $\mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
, we denote
$\mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
, we denote
![]() $f\thicksim g$
if
$f\thicksim g$
if
![]() $f-g$
is null-homotopic. We denote by
$f-g$
is null-homotopic. We denote by
![]() $\mathop{\textrm{K}}\nolimits \!(\mathcal{A})$
the homotopic category, that is, the category consisting of complexes such that the morphism set between
$\mathop{\textrm{K}}\nolimits \!(\mathcal{A})$
the homotopic category, that is, the category consisting of complexes such that the morphism set between
![]() $X,Y\in \mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
is given by
$X,Y\in \mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
is given by
![]() ${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\mathcal{A})}(X,Y)={\textrm{Hom}}_{\mathop{\textrm{C}}\nolimits \!(\mathcal{A})}(X,Y)/\thicksim$
. Furthermore, there is a corresponding derived category
${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\mathcal{A})}(X,Y)={\textrm{Hom}}_{\mathop{\textrm{C}}\nolimits \!(\mathcal{A})}(X,Y)/\thicksim$
. Furthermore, there is a corresponding derived category
![]() $\mathop{\textrm{D}}\nolimits \!(\mathcal{A})$
, which is also triangulated.
$\mathop{\textrm{D}}\nolimits \!(\mathcal{A})$
, which is also triangulated.
In order to obtain an abelian model structure, we have to introduce the following classes in
![]() $\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
.
$\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
.
Definition 4.4. ([Reference Gillespie12]). Let
![]() $(\mathcal{A}, \mathcal{B})$
be a cotorsion pair on an abelian category
$(\mathcal{A}, \mathcal{B})$
be a cotorsion pair on an abelian category
![]() $\mathcal{C}$
. Let
$\mathcal{C}$
. Let
![]() $X$
be a complex.
$X$
be a complex.
-
(1)
 $X$
is called an
$X$
is called an
 $\mathcal{A}$
complex if it is exact and
$\mathcal{A}$
complex if it is exact and
 $Z_n(X)\in \mathcal{A}$
for all
$Z_n(X)\in \mathcal{A}$
for all
 $n$
.
$n$
. -
(2)
 $X$
is called a
$X$
is called a
 $\mathcal{B}$
complex if it is exact and
$\mathcal{B}$
complex if it is exact and
 $Z_n(X)\in \mathcal{B}$
for all
$Z_n(X)\in \mathcal{B}$
for all
 $n$
.
$n$
. -
(3)
 $X$
is called a
$X$
is called a
 $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
 $\mathcal{A}$
complex if
$\mathcal{A}$
complex if
 $X_n\in \mathcal{A}$
for each
$X_n\in \mathcal{A}$
for each
 $n$
, and
$n$
, and
 ${\textrm{Hom}}(X,B)$
is exact whenever
${\textrm{Hom}}(X,B)$
is exact whenever
 $B$
is a
$B$
is a
 $\mathcal{B}$
complex.
$\mathcal{B}$
complex.
-
(4)
 $X$
is called a
$X$
is called a
 $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
 $\mathcal{B}$
complex if
$\mathcal{B}$
complex if
 $X_n\in \mathcal{B}$
for each
$X_n\in \mathcal{B}$
for each
 $n$
, and
$n$
, and
 ${\textrm{Hom}}(A,X)$
is exact whenever
${\textrm{Hom}}(A,X)$
is exact whenever
 $A$
is an
$A$
is an
 $\mathcal{A}$
complex.
$\mathcal{A}$
complex.
We denote the class of
![]() $\mathcal{A}$
complexes by
$\mathcal{A}$
complexes by
![]() $\tilde{\mathcal{A}}$
and the class of
$\tilde{\mathcal{A}}$
and the class of
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{A}$
complexes by
$\mathcal{A}$
complexes by
![]() $dg\tilde{\mathcal{A}}$
. Similarly, the class of
$dg\tilde{\mathcal{A}}$
. Similarly, the class of
![]() $\mathcal{B}$
complexes is denoted by
$\mathcal{B}$
complexes is denoted by
![]() $\tilde{\mathcal{B}}$
and the class of
$\tilde{\mathcal{B}}$
and the class of
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{B}$
complexes is denoted by
$\mathcal{B}$
complexes is denoted by
![]() $dg\tilde{\mathcal{B}}$
.
$dg\tilde{\mathcal{B}}$
.
Inspired by [Reference Bazzoni5, Theorem 2.5], we present the following theorem.
Theorem 4.5.
Suppose that
![]() $\mathcal{T}$
is a generalized tilting subcategory of
$\mathcal{T}$
is a generalized tilting subcategory of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. Let
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. Let
![]() $\mathcal{A}=$
$\mathcal{A}=$
![]() $^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})$
,
$^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}})$
,
![]() $\mathcal{B}=\mathcal{T}^{\perp _{\infty }}$
. Then there is an abelian model structure on
$\mathcal{B}=\mathcal{T}^{\perp _{\infty }}$
. Then there is an abelian model structure on
![]() $\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
given as follows:
$\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
given as follows:
-
(1) Weak equivalences are quasi-isomorphisms,
-
(2) Cofibrations (trivial cofibrations) consist of all the monomorphisms
 $f$
such that
$f$
such that
 ${\textrm{Ext}}^1_{\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\mathop{\textrm{Coker}}\nolimits f,X)=0$
for any
${\textrm{Ext}}^1_{\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\mathop{\textrm{Coker}}\nolimits f,X)=0$
for any
 $X\in \tilde{\mathcal{B}}$
(
$X\in \tilde{\mathcal{B}}$
(
 $\mathop{\textrm{Coker}}\nolimits f\in \tilde{\mathcal{A}}$
),
$\mathop{\textrm{Coker}}\nolimits f\in \tilde{\mathcal{A}}$
),
-
(3) Fibrations (trivial fibrations) consist of all the epimorphisms
 $g$
such that
$g$
such that
 ${\textrm{Ext}}^1_{\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(X, \mathop{\textrm{Ker}}\nolimits g)=0$
for any
${\textrm{Ext}}^1_{\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(X, \mathop{\textrm{Ker}}\nolimits g)=0$
for any
 $X\in \tilde{\mathcal{A}}$
(
$X\in \tilde{\mathcal{A}}$
(
 $\mathop{\textrm{Ker}}\nolimits g\in \tilde{\mathcal{B}})$
.
$\mathop{\textrm{Ker}}\nolimits g\in \tilde{\mathcal{B}})$
.
The homotopy category of this model category is
![]() $\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
.
$\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
.
Proof. Since
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
is a Grothendieck category, it is a bicomplete abelian category by [Reference Stenström30, Chapter V] and [Reference Martínez-Villa and Ortiz-Morales20, Section 1.2]. Because
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
is a Grothendieck category, it is a bicomplete abelian category by [Reference Stenström30, Chapter V] and [Reference Martínez-Villa and Ortiz-Morales20, Section 1.2]. Because
![]() $(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}),\mathcal{T}^{\perp _{\infty }})$
is a hereditary and complete cotorsion pair by Theorem 4.3, it follows from [Reference Yang and Ding34, Theorem 2.4] that there are two induced complete cotorsion pairs (
$(^{\perp _{\infty }}({\mathcal{T}^{\perp _{\infty }}}),\mathcal{T}^{\perp _{\infty }})$
is a hereditary and complete cotorsion pair by Theorem 4.3, it follows from [Reference Yang and Ding34, Theorem 2.4] that there are two induced complete cotorsion pairs (
![]() $\tilde{\mathcal{A}}$
,
$\tilde{\mathcal{A}}$
,
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{B}$
) and (
$\mathcal{B}$
) and (
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{A}$
,
$\mathcal{A}$
,
![]() $\tilde{\mathcal{B}}$
). So we claim that
$\tilde{\mathcal{B}}$
). So we claim that
![]() $X\in$
$X\in$
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{A}$
if and only if
$\mathcal{A}$
if and only if
![]() ${\textrm{Ext}}^1_{\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(X,B)=0$
for any
${\textrm{Ext}}^1_{\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(X,B)=0$
for any
![]() $B\in \tilde{\mathcal{B}}$
and
$B\in \tilde{\mathcal{B}}$
and
![]() $Y\in$
$Y\in$
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{B}$
if and only if
$\mathcal{B}$
if and only if
![]() ${\textrm{Ext}}^1_{\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(A, Y)=0$
for any
${\textrm{Ext}}^1_{\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(A, Y)=0$
for any
![]() $A\in \tilde{\mathcal{A}}$
.
$A\in \tilde{\mathcal{A}}$
.
Next, we know from [Reference Gillespie13, Corollary 3.8] that there is an abelian model structure on
![]() $\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
. Furthermore, weak equivalences, cofibrantions, and fibrations are described exactly as in the statements. Observe that exact
$\mathop{\textrm{C}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
. Furthermore, weak equivalences, cofibrantions, and fibrations are described exactly as in the statements. Observe that exact
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{A}$
complexes are exactly
$\mathcal{A}$
complexes are exactly
![]() $\mathcal{A}$
complexes by [Reference Yang and Ding34, Theorem 2.5]. In particular,
$\mathcal{A}$
complexes by [Reference Yang and Ding34, Theorem 2.5]. In particular,
![]() $f\,:\,M\to N$
is a trivial cofibration if and only if there is an exact sequence
$f\,:\,M\to N$
is a trivial cofibration if and only if there is an exact sequence
![]() $0 \to M\stackrel{f}{\longrightarrow } N\to L\to 0$
such that
$0 \to M\stackrel{f}{\longrightarrow } N\to L\to 0$
such that
![]() $f$
is a quasi-isomorphism and
$f$
is a quasi-isomorphism and
![]() $\mathop{\textrm{Coker}}\nolimits f\in$
$\mathop{\textrm{Coker}}\nolimits f\in$
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{A}$
if and only if there is an exact sequence
$\mathcal{A}$
if and only if there is an exact sequence
![]() $0 \to M\stackrel{f}{\longrightarrow } N\to L\to 0$
such that
$0 \to M\stackrel{f}{\longrightarrow } N\to L\to 0$
such that
![]() $L\in \tilde{\mathcal{A}}$
. The case for trivial fibrations can be shown similarly. The last statement follows from [Reference Gillespie14, Introduction].
$L\in \tilde{\mathcal{A}}$
. The case for trivial fibrations can be shown similarly. The last statement follows from [Reference Gillespie14, Introduction].
According to [Reference Hovey17, Reference Hovey18], suppose that an abelian category
![]() $\mathcal{A}$
has a model structure,
$\mathcal{A}$
has a model structure,
![]() $X$
is trivial if
$X$
is trivial if
![]() $0\to X$
is a weak equivalence,
$0\to X$
is a weak equivalence,
![]() $X$
is cofibrant if
$X$
is cofibrant if
![]() $0\to X$
is a cofibration and
$0\to X$
is a cofibration and
![]() $X$
is fibrant if
$X$
is fibrant if
![]() $X\to 0$
is a fibration.
$X\to 0$
is a fibration.
Corollary 4.6. In the notations of Theorem 4.5, then we have the following statements.
-
(1)
 $X$
is trivial if and only if
$X$
is trivial if and only if
 $X$
is exact.
$X$
is exact.
-
(2)
 $C$
is a cofibrant if and only if
$C$
is a cofibrant if and only if
 $C\in$
$C\in$
 $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
 $\mathcal{A}$
.
$\mathcal{A}$
. -
(3)
 $F$
is a fibrant if and only if
$F$
is a fibrant if and only if
 $F\in$
$F\in$
 $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
 $\mathcal{B}$
if and only if
$\mathcal{B}$
if and only if
 $F$
has all the terms in
$F$
has all the terms in
 $\mathcal{B}$
.
$\mathcal{B}$
.
Proof. (1), (2) and the first equivalence of (3) follow from Theorem 4.5 easily. We only need to show that
![]() $F\in$
$F\in$
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{B}$
if and only if
$\mathcal{B}$
if and only if
![]() $F$
all the terms in
$F$
all the terms in
![]() $\mathcal{B}$
. If
$\mathcal{B}$
. If
![]() $F\in$
$F\in$
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{B}$
, then
$\mathcal{B}$
, then
![]() $F$
has all the terms in
$F$
has all the terms in
![]() $\mathcal{B}$
. Conversely, if
$\mathcal{B}$
. Conversely, if
![]() $F$
has all the terms in
$F$
has all the terms in
![]() $\mathcal{B}$
, since (
$\mathcal{B}$
, since (
![]() $\tilde{\mathcal{A}}$
,
$\tilde{\mathcal{A}}$
,
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{B}$
) is a complete cotorsion pair by the proof of Theorem 4.5, there is an exact sequence
$\mathcal{B}$
) is a complete cotorsion pair by the proof of Theorem 4.5, there is an exact sequence
![]() $0\to F\to B\to A\to 0$
with
$0\to F\to B\to A\to 0$
with
![]() $B\in$
$B\in$
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{B}$
and
$\mathcal{B}$
and
![]() $A\in \tilde{\mathcal{A}}$
. The fact that the cotorsion pair (
$A\in \tilde{\mathcal{A}}$
. The fact that the cotorsion pair (
![]() $\mathcal{A}$
,
$\mathcal{A}$
,
![]() $\mathcal{B}$
) is hereditary implies that
$\mathcal{B}$
) is hereditary implies that
![]() $A_n\in \mathcal{B}$
for each
$A_n\in \mathcal{B}$
for each
![]() $n$
. For any
$n$
. For any
![]() $T\in \mathcal{T}$
and any
$T\in \mathcal{T}$
and any
![]() $i\in \mathbb{Z}$
, since
$i\in \mathbb{Z}$
, since
![]() $T$
has finite projective dimension, we have that
$T$
has finite projective dimension, we have that
![]() ${\textrm{Ext}}^{j\geqslant 1}_{\mathcal{C}}(T, Z_i(A))=0$
by dimension shifting. Thus,
${\textrm{Ext}}^{j\geqslant 1}_{\mathcal{C}}(T, Z_i(A))=0$
by dimension shifting. Thus,
![]() $A\in \tilde{\mathcal{B}}$
. Let
$A\in \tilde{\mathcal{B}}$
. Let
![]() $X\in \tilde{\mathcal{A}}$
. Since all components of
$X\in \tilde{\mathcal{A}}$
. Since all components of
![]() $F$
are in
$F$
are in
![]() $\mathcal{B}$
and all components of
$\mathcal{B}$
and all components of
![]() $X$
are in
$X$
are in
![]() $\mathcal{A}$
, we deduce that the sequence
$\mathcal{A}$
, we deduce that the sequence
![]() $0\to{\textrm{Hom}}(X,F)\to{\textrm{Hom}}(X,B)\to{\textrm{Hom}}(X,A)\to 0$
is exact. Observe that
$0\to{\textrm{Hom}}(X,F)\to{\textrm{Hom}}(X,B)\to{\textrm{Hom}}(X,A)\to 0$
is exact. Observe that
![]() $A\in \tilde{\mathcal{B}}\subseteq$
$A\in \tilde{\mathcal{B}}\subseteq$
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{B}$
and
$\mathcal{B}$
and
![]() $B\in$
$B\in$
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{B}$
. The complexes
$\mathcal{B}$
. The complexes
![]() ${\textrm{Hom}}(X,B)$
and
${\textrm{Hom}}(X,B)$
and
![]() ${\textrm{Hom}}(X,A)$
are exact. So is
${\textrm{Hom}}(X,A)$
are exact. So is
![]() ${\textrm{Hom}}(X,F)$
. Therefore,
${\textrm{Hom}}(X,F)$
. Therefore,
![]() $F\in$
$F\in$
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{B}$
.
$\mathcal{B}$
.
Corollary 4.7.
In the notations of Theorem 4.5, let
![]() $F$
be a complex with terms in
$F$
be a complex with terms in
![]() $\mathcal{B}$
and let
$\mathcal{B}$
and let
![]() $C$
be cofibrant in the model structure induced by
$C$
be cofibrant in the model structure induced by
![]() $\mathcal{T}$
. Then there is a natural isomorphism
$\mathcal{T}$
. Then there is a natural isomorphism
In particular, this applies to the complexes
![]() $C$
bounded below and with terms in
$C$
bounded below and with terms in
![]() $\mathcal{A}$
.
$\mathcal{A}$
.
Proof. We know by Corollary 4.6(3) that
![]() $F$
is a fibrant. Then it follows from [Reference Gillespie14] that
$F$
is a fibrant. Then it follows from [Reference Gillespie14] that
![]() ${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(C,F)\cong{\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(C,F)$
. In particular, if
${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(C,F)\cong{\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(C,F)$
. In particular, if
![]() $C$
is a bounded below complex with terms in
$C$
is a bounded below complex with terms in
![]() $\mathcal{A}$
, then
$\mathcal{A}$
, then
![]() $C\in$
$C\in$
![]() $\mathop{\textrm{dg}}\nolimits$
-
$\mathop{\textrm{dg}}\nolimits$
-
![]() $\mathcal{A}$
by [Reference Gillespie12, Lemma 3.4(1)]. It implies that
$\mathcal{A}$
by [Reference Gillespie12, Lemma 3.4(1)]. It implies that
![]() $C$
is a cofibrant by Corollary 4.6(2). So the equivalence also applies to
$C$
is a cofibrant by Corollary 4.6(2). So the equivalence also applies to
![]() $C$
.
$C$
.
5. A t-structure induced by a generalized tilting subcategory
In this section, we mainly show that there exists a t-structure on the derived category
![]() $\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
, relating a generalized tilting subcategory
$\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
, relating a generalized tilting subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. For the sake of completeness, let us recall the definition of a t-structure.
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. For the sake of completeness, let us recall the definition of a t-structure.
Definition 5.1. ([Reference Beilinson, Bernstein and Deligne7]). Let
![]() $\mathcal{D}$
be a triangulated category. A t-structure on
$\mathcal{D}$
be a triangulated category. A t-structure on
![]() $\mathcal{D}$
is a pair of full subcategories (
$\mathcal{D}$
is a pair of full subcategories (
![]() $\mathcal{D}^{\leqslant 0}$
,
$\mathcal{D}^{\leqslant 0}$
,
![]() $\mathcal{D}^{\geqslant 0}$
) with the following properties: write
$\mathcal{D}^{\geqslant 0}$
) with the following properties: write
![]() $\mathcal{D}^{\leqslant n}=\Sigma ^{-n}\mathcal{D}^{\leqslant 0}$
and
$\mathcal{D}^{\leqslant n}=\Sigma ^{-n}\mathcal{D}^{\leqslant 0}$
and
![]() $\mathcal{D}^{\geqslant n}=\Sigma ^{-n}\mathcal{D}^{\geqslant 0}$
for
$\mathcal{D}^{\geqslant n}=\Sigma ^{-n}\mathcal{D}^{\geqslant 0}$
for
![]() $n\in \mathbb{Z}$
.
$n\in \mathbb{Z}$
.
-
(1)
 ${\textrm{Hom}}_{\mathcal{D}}(X,Y)=0$
for all
${\textrm{Hom}}_{\mathcal{D}}(X,Y)=0$
for all
 $X\in \mathcal{D}^{\leqslant 0}$
and
$X\in \mathcal{D}^{\leqslant 0}$
and
 $Y\in \mathcal{D}^{\geqslant 1}$
.
$Y\in \mathcal{D}^{\geqslant 1}$
. -
(2)
 $\mathcal{D}^{\leqslant 0}\subseteq \mathcal{D}^{\leqslant 1}$
and
$\mathcal{D}^{\leqslant 0}\subseteq \mathcal{D}^{\leqslant 1}$
and
 $\mathcal{D}^{\geqslant 0}\supseteq \mathcal{D}^{\geqslant 1}$
.
$\mathcal{D}^{\geqslant 0}\supseteq \mathcal{D}^{\geqslant 1}$
. -
(3) For every object
 $Z\in \mathcal{D}$
there is a distinguished triangle
$Z\in \mathcal{D}$
there is a distinguished triangle
 $X\to Z\to Y\to \Sigma X$
with
$X\to Z\to Y\to \Sigma X$
with
 $X\in \mathcal{D}^{\leqslant 0}$
and
$X\in \mathcal{D}^{\leqslant 0}$
and
 $Y\in \mathcal{D}^{\geqslant 1}$
.
$Y\in \mathcal{D}^{\geqslant 1}$
.
Notation 5.2.
Suppose that
![]() $\mathcal{T}$
is a generalized tilting subcategory of
$\mathcal{T}$
is a generalized tilting subcategory of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. For any
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
. For any
![]() $k\in \mathbb{Z}$
, we denote by
$k\in \mathbb{Z}$
, we denote by
![]() $\mathcal{D}^{\leqslant k}_{\mathcal{T}}$
and
$\mathcal{D}^{\leqslant k}_{\mathcal{T}}$
and
![]() $\mathcal{D}^{\geqslant k}_{\mathcal{T}}$
the full subcategories of
$\mathcal{D}^{\geqslant k}_{\mathcal{T}}$
the full subcategories of
![]() $\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
given by
$\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
given by
Let
![]() $\mathcal{A}$
be an abelian category and
$\mathcal{A}$
be an abelian category and
![]() $\mathcal{F}$
be a class of objects in
$\mathcal{F}$
be a class of objects in
![]() $\mathcal{A}$
. Then a morphism
$\mathcal{A}$
. Then a morphism
![]() $\varphi \,:\, F\to M$
of
$\varphi \,:\, F\to M$
of
![]() $\mathcal{A}$
is called an
$\mathcal{A}$
is called an
![]() $\mathcal{F}$
-precover of
$\mathcal{F}$
-precover of
![]() $M$
if
$M$
if
![]() $F\in \mathcal{F}$
and
$F\in \mathcal{F}$
and
![]() ${\textrm{Hom}}_{\mathcal{A}}(F^{\prime},F)\to{\textrm{Hom}}_{\mathcal{A}}(F^{\prime},M)\to 0$
is exact for all
${\textrm{Hom}}_{\mathcal{A}}(F^{\prime},F)\to{\textrm{Hom}}_{\mathcal{A}}(F^{\prime},M)\to 0$
is exact for all
![]() $F^{\prime}\in \mathcal{F}$
. If every object of
$F^{\prime}\in \mathcal{F}$
. If every object of
![]() $\mathcal{A}$
has an
$\mathcal{A}$
has an
![]() $\mathcal{F}$
-precover,
$\mathcal{F}$
-precover,
![]() $\mathcal{F}$
is said to be precovering [Reference Enochs and Jenda11]. Given
$\mathcal{F}$
is said to be precovering [Reference Enochs and Jenda11]. Given
![]() $k\in \mathbb{Z}$
, we say that a complex
$k\in \mathbb{Z}$
, we say that a complex
![]() $X\in \mathop{\textrm{C}}\nolimits ^{[k,\infty ]}(\mathcal{F})$
if
$X\in \mathop{\textrm{C}}\nolimits ^{[k,\infty ]}(\mathcal{F})$
if
![]() $X_i=0$
for
$X_i=0$
for
![]() $i\lt k$
and
$i\lt k$
and
![]() $X_i\in \mathcal{F}$
for
$X_i\in \mathcal{F}$
for
![]() $i\geqslant k$
.
$i\geqslant k$
.
Lemma 5.3.
Suppose that
![]() $\mathcal{A}$
is an abelian category and
$\mathcal{A}$
is an abelian category and
![]() $\mathcal{F}$
is a class of objects in
$\mathcal{F}$
is a class of objects in
![]() $\mathcal{A}$
. If
$\mathcal{A}$
. If
![]() $\mathcal{F}$
is precovering, then for every complex
$\mathcal{F}$
is precovering, then for every complex
![]() $X$
in
$X$
in
![]() $\mathop{\textrm{D}}\nolimits \!(\mathcal{A})$
and every
$\mathop{\textrm{D}}\nolimits \!(\mathcal{A})$
and every
![]() $k\in \mathbb{Z}$
, there is a chain map
$k\in \mathbb{Z}$
, there is a chain map
![]() $f\,:\, F\to X$
with
$f\,:\, F\to X$
with
![]() $F\in \mathop{\textrm{C}}\nolimits ^{[k,\infty ]}(\mathcal{F})$
such that
$F\in \mathop{\textrm{C}}\nolimits ^{[k,\infty ]}(\mathcal{F})$
such that
![]() ${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\mathcal{A})}(\Sigma ^iF,f)$
is an isomorphism for any
${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\mathcal{A})}(\Sigma ^iF,f)$
is an isomorphism for any
![]() $F\in \mathcal{F}$
and any
$F\in \mathcal{F}$
and any
![]() $i\geqslant k$
.
$i\geqslant k$
.
Proof. Given a complex
![]() $X\,:\!=\, \cdots \to X_{n+1}\stackrel{d_{n+1}^X}{\longrightarrow } X_n\stackrel{d_{n}^X}{\longrightarrow } X_{n-1}\to \cdots$
with
$X\,:\!=\, \cdots \to X_{n+1}\stackrel{d_{n+1}^X}{\longrightarrow } X_n\stackrel{d_{n}^X}{\longrightarrow } X_{n-1}\to \cdots$
with
![]() $X_n\in \mathcal{A}$
. We will inductively construct a chain map
$X_n\in \mathcal{A}$
. We will inductively construct a chain map
![]() $f\,:\, X\to F$
$f\,:\, X\to F$

such that
![]() $F_i\in \mathcal{F}$
for
$F_i\in \mathcal{F}$
for
![]() $i\geqslant 0$
. Consider an
$i\geqslant 0$
. Consider an
![]() $\mathcal{F}$
-precover of
$\mathcal{F}$
-precover of
![]() $\mathop{\textrm{Ker}}\nolimits d_{k}^X$
,
$\mathop{\textrm{Ker}}\nolimits d_{k}^X$
,
![]() $F_k\stackrel{\varphi _k}{\longrightarrow } \mathop{\textrm{Ker}}\nolimits d_{k}^X$
, and let
$F_k\stackrel{\varphi _k}{\longrightarrow } \mathop{\textrm{Ker}}\nolimits d_{k}^X$
, and let
![]() $f_k$
be the composition of
$f_k$
be the composition of
![]() $\varphi _k$
with the inclusion
$\varphi _k$
with the inclusion
![]() $\mathop{\textrm{Ker}}\nolimits d_{k}^X\to X_k$
. By induction construct
$\mathop{\textrm{Ker}}\nolimits d_{k}^X\to X_k$
. By induction construct
![]() $f_{i+1}\,:\, F_{i+1}\to X_{i+1}$
as follows. Having defined
$f_{i+1}\,:\, F_{i+1}\to X_{i+1}$
as follows. Having defined
![]() $f_{i}\,:\, F_{i}\to X_{i}$
and
$f_{i}\,:\, F_{i}\to X_{i}$
and
![]() $d_{i}^F\,:\, F_i\to F_{i-1}$
. Let
$d_{i}^F\,:\, F_i\to F_{i-1}$
. Let
![]() $\lambda _i\,:\, K_i\to F_i$
be the kernel of
$\lambda _i\,:\, K_i\to F_i$
be the kernel of
![]() $d_{i}^F$
and let
$d_{i}^F$
and let
![]() $g_i=f_i\lambda _i$
. Consider the pullback
$g_i=f_i\lambda _i$
. Consider the pullback
![]() $P_{i+1}$
of the maps
$P_{i+1}$
of the maps
![]() $g_i$
and
$g_i$
and
![]() $d_{i+1}^X$
. Let
$d_{i+1}^X$
. Let
![]() $\varphi _{i+1}\,:\,F_{i+1}\to P_{i+1}$
be an
$\varphi _{i+1}\,:\,F_{i+1}\to P_{i+1}$
be an
![]() $\mathcal{F}$
-precover of
$\mathcal{F}$
-precover of
![]() $P_{i+1}$
and let
$P_{i+1}$
and let
![]() $f_{i+1}$
be the obvious composition. All the maps used in the inductive step are depicted in the following diagram
$f_{i+1}$
be the obvious composition. All the maps used in the inductive step are depicted in the following diagram

where
![]() $d_{i+1}^F=\lambda _i \alpha _{i+1} \varphi _{i+1}$
. It is easy to see that
$d_{i+1}^F=\lambda _i \alpha _{i+1} \varphi _{i+1}$
. It is easy to see that
![]() $F$
is a complex with all terms in
$F$
is a complex with all terms in
![]() $\mathcal{F}$
and
$\mathcal{F}$
and
![]() $f$
is a chain map between
$f$
is a chain map between
![]() $F$
and
$F$
and
![]() $X$
. Now we claim that
$X$
. Now we claim that
![]() ${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\mathcal{A})}(\Sigma ^iF^{\prime},X)=0$
for any
${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\mathcal{A})}(\Sigma ^iF^{\prime},X)=0$
for any
![]() $F^{\prime}\in \mathcal{F}$
and any
$F^{\prime}\in \mathcal{F}$
and any
![]() $i\geqslant k$
. If
$i\geqslant k$
. If
![]() $i\geqslant k$
, given a map
$i\geqslant k$
, given a map
![]() $h\,:\, \Sigma ^iF^{\prime}\to X$
in
$h\,:\, \Sigma ^iF^{\prime}\to X$
in
![]() $\mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
, our task is to prove that
$\mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
, our task is to prove that
(a)
![]() $h$
factors through
$h$
factors through
![]() $f\,:\, F \to X$
, and
$f\,:\, F \to X$
, and
(b) If
![]() $h$
is null-homotopic, so is any such factorization
$h$
is null-homotopic, so is any such factorization
![]() $t\,:\, \Sigma ^iF^{\prime}\to F$
.
$t\,:\, \Sigma ^iF^{\prime}\to F$
.
Regarding (a), since
![]() $h$
is a chain map,
$h$
is a chain map,
![]() $d_{i}^Xh_i=0$
. Using the pullback property of
$d_{i}^Xh_i=0$
. Using the pullback property of
![]() $P_{i}$
, we construct a map
$P_{i}$
, we construct a map
![]() $\theta _{i}\,:\, F^{\prime}\to P_{i}$
such that
$\theta _{i}\,:\, F^{\prime}\to P_{i}$
such that
![]() $\beta _{i}\theta _{i}=h_{i}$
and
$\beta _{i}\theta _{i}=h_{i}$
and
![]() $\alpha _{i}\theta _{i}=0$
. We can factor
$\alpha _{i}\theta _{i}=0$
. We can factor
![]() $\theta _{i}$
further through the
$\theta _{i}$
further through the
![]() $\mathcal{F}$
-precover
$\mathcal{F}$
-precover
![]() $\varphi _{i}\,:\,F_{i}\to P_{i}$
to obtain a map
$\varphi _{i}\,:\,F_{i}\to P_{i}$
to obtain a map
![]() $t_{i}\,:\, F^{\prime}\to F_{i}$
. Thus,
$t_{i}\,:\, F^{\prime}\to F_{i}$
. Thus,
![]() $d_{i}^Ft_{i}=\lambda _{i-1} \alpha _{i} \varphi _{i}t_{i}=\lambda _{i-1} \alpha _{i}\theta _{i}=0$
. It means that
$d_{i}^Ft_{i}=\lambda _{i-1} \alpha _{i} \varphi _{i}t_{i}=\lambda _{i-1} \alpha _{i}\theta _{i}=0$
. It means that
![]() $t\,:\, \Sigma ^iF^{\prime}\to F$
is a chain map. On the other hand, as
$t\,:\, \Sigma ^iF^{\prime}\to F$
is a chain map. On the other hand, as
![]() $f_it_i=\beta _i\varphi _it_i=\beta _i\theta _i=h_i$
, we conclude that
$f_it_i=\beta _i\varphi _it_i=\beta _i\theta _i=h_i$
, we conclude that
![]() $h=ft$
.
$h=ft$
.
Regarding (b), assume that
![]() $h$
is null-homotopic and
$h$
is null-homotopic and
![]() $h=ft$
for some
$h=ft$
for some
![]() $t\,:\, \Sigma ^iF^{\prime}\to F$
in
$t\,:\, \Sigma ^iF^{\prime}\to F$
in
![]() $\mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
, we will show that
$\mathop{\textrm{C}}\nolimits \!(\mathcal{A})$
, we will show that
![]() $t$
is also null-homotopic. Since
$t$
is also null-homotopic. Since
![]() $h$
is null-homotopic, there exists a map
$h$
is null-homotopic, there exists a map
![]() $s_{i+1}\,:\, F^{\prime}\to X_{i+1}$
such that
$s_{i+1}\,:\, F^{\prime}\to X_{i+1}$
such that
![]() $d_{i+1}^Xs_{i+1}=h_i$
. Note that
$d_{i+1}^Xs_{i+1}=h_i$
. Note that
![]() $t$
is a chain map and
$t$
is a chain map and
![]() $\lambda _i\,:\, K_i\to F_i$
is the kernel of
$\lambda _i\,:\, K_i\to F_i$
is the kernel of
![]() $d_{i}^F$
. We get a map
$d_{i}^F$
. We get a map
![]() $\gamma _i\,:\, F^{\prime}\to K_i$
with
$\gamma _i\,:\, F^{\prime}\to K_i$
with
![]() $\lambda _i\gamma _i=t_i$
. Then
$\lambda _i\gamma _i=t_i$
. Then
![]() $g_i\gamma _i=f_i\lambda _i\gamma _i=f_it_i=h_i=d_{i+1}^Xs_{i+1}$
. By the pullback property of
$g_i\gamma _i=f_i\lambda _i\gamma _i=f_it_i=h_i=d_{i+1}^Xs_{i+1}$
. By the pullback property of
![]() $P_{i+1}$
, there is a map
$P_{i+1}$
, there is a map
![]() $\delta _{i+1}\,:\, F^{\prime}\to P_{i+1}$
such that
$\delta _{i+1}\,:\, F^{\prime}\to P_{i+1}$
such that
![]() $s_{i+1}=\beta _{i+1}\delta _{i+1}$
and
$s_{i+1}=\beta _{i+1}\delta _{i+1}$
and
![]() $\gamma _i=\alpha _{i+1}\delta _{i+1}$
. We further factor
$\gamma _i=\alpha _{i+1}\delta _{i+1}$
. We further factor
![]() $\delta _{i+1}$
through the
$\delta _{i+1}$
through the
![]() $\mathcal{F}$
-precover
$\mathcal{F}$
-precover
![]() $\varphi _{i+1}\,:\,F_{i+1}\to P_{i+1}$
to obtain a map
$\varphi _{i+1}\,:\,F_{i+1}\to P_{i+1}$
to obtain a map
![]() $\eta _{i+1}\,:\, F^{\prime}\to F_{i+1}$
. Then
$\eta _{i+1}\,:\, F^{\prime}\to F_{i+1}$
. Then
![]() $d_{i+1}^F\eta _{i+1}=\lambda _i \alpha _{i+1} \varphi _{i+1}\eta _{i+1}=\lambda _i \alpha _{i+1}\delta _{i+1}=\lambda _i\gamma _i=t_i$
. So
$d_{i+1}^F\eta _{i+1}=\lambda _i \alpha _{i+1} \varphi _{i+1}\eta _{i+1}=\lambda _i \alpha _{i+1}\delta _{i+1}=\lambda _i\gamma _i=t_i$
. So
![]() $t$
is null-homotopic, and we are done.
$t$
is null-homotopic, and we are done.
Next, we can give a description of the complexes in
![]() $\mathcal{D}^{\leqslant k}_{\mathcal{T}}$
.
$\mathcal{D}^{\leqslant k}_{\mathcal{T}}$
.
Proposition 5.4.
Let
![]() $\mathcal{T}$
be a generalized tilting subcategory of
$\mathcal{T}$
be a generalized tilting subcategory of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
,
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
,
![]() $k\in \mathbb{Z}$
and
$k\in \mathbb{Z}$
and
![]() $\mathcal{D}^{\leqslant k}_{\mathcal{T}}$
as in Notation 5.2. For a complex in
$\mathcal{D}^{\leqslant k}_{\mathcal{T}}$
as in Notation 5.2. For a complex in
![]() $\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
, the following statements are equivalent.
$\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
, the following statements are equivalent.
-
(1)
 $X\in \mathcal{D}^{\leqslant k}_{\mathcal{T}}$
.
$X\in \mathcal{D}^{\leqslant k}_{\mathcal{T}}$
. -
(2)
 $X$
is isomorphic in
$X$
is isomorphic in
 $\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
to a complex
$\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
to a complex
 $B$
of the form
with
$B$
of the form
with \begin{equation*}\cdots \to B_{k+2}\to B_{k+1}\to B_{k}\to 0\to \cdots\end{equation*}
\begin{equation*}\cdots \to B_{k+2}\to B_{k+1}\to B_{k}\to 0\to \cdots\end{equation*}
 $B_i\in \mathcal{T}^{\perp _{\infty }}$
for every
$B_i\in \mathcal{T}^{\perp _{\infty }}$
for every
 $i\geqslant k$
.
$i\geqslant k$
.
-
(3)
 $X$
is isomorphic in
$X$
is isomorphic in
 $\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
to a complex
$\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
to a complex
 $T$
as in (2), but with
$T$
as in (2), but with
 $T_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
for every
$T_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
for every
 $i\geqslant k$
.
$i\geqslant k$
.
Proof. (3)
![]() $\Rightarrow$
(2) is obvious.
$\Rightarrow$
(2) is obvious.
(2)
![]() $\Rightarrow$
(1) For any
$\Rightarrow$
(1) For any
![]() $T\in \mathcal{T}$
and
$T\in \mathcal{T}$
and
![]() $i\lt k$
, we have that
$i\lt k$
, we have that
![]() ${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT,X)={\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT,B)$
${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT,X)={\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT,B)$
![]() $={\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT,B)=\mathop{\textrm{H}}\nolimits _i{\textrm{Hom}}(T,B)=0$
by Corollary 4.7. So
$={\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT,B)=\mathop{\textrm{H}}\nolimits _i{\textrm{Hom}}(T,B)=0$
by Corollary 4.7. So
![]() $X\in \mathcal{D}^{\leqslant k}_{\mathcal{T}}$
.
$X\in \mathcal{D}^{\leqslant k}_{\mathcal{T}}$
.
(1)
![]() $\Rightarrow$
(3) Every complex
$\Rightarrow$
(3) Every complex
![]() $X$
has a fibrant replacement in the model structure defined by the generalized tilting subcategory
$X$
has a fibrant replacement in the model structure defined by the generalized tilting subcategory
![]() $\mathcal{T}$
, by Corollary 4.6 we can assume that
$\mathcal{T}$
, by Corollary 4.6 we can assume that
![]() $X$
has terms in
$X$
has terms in
![]() $\mathcal{B}$
. It follows from Proposition 3.1 that every term of
$\mathcal{B}$
. It follows from Proposition 3.1 that every term of
![]() $X$
has an
$X$
has an
![]() $\mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
-precover. Then by Lemma 5.3 there is a chain map
$\mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
-precover. Then by Lemma 5.3 there is a chain map
![]() $f\,:\, T\to X$
with
$f\,:\, T\to X$
with
![]() $T\in \mathop{\textrm{C}}\nolimits ^{[k,\infty ]}(\mathop{\textrm{Add}}\nolimits \!(\mathcal{T}))$
and
$T\in \mathop{\textrm{C}}\nolimits ^{[k,\infty ]}(\mathop{\textrm{Add}}\nolimits \!(\mathcal{T}))$
and
![]() ${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\mathcal{A})}(\Sigma ^iT^{\prime},f)$
is an isomorphism for any
${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\mathcal{A})}(\Sigma ^iT^{\prime},f)$
is an isomorphism for any
![]() $T^{\prime}\in \mathcal{T}$
and any
$T^{\prime}\in \mathcal{T}$
and any
![]() $i\geqslant k$
. For
$i\geqslant k$
. For
![]() $i\lt k$
. By assumption on
$i\lt k$
. By assumption on
![]() $X$
we know that
$X$
we know that
![]() ${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT^{\prime},X)=0$
for any
${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT^{\prime},X)=0$
for any
![]() $T^{\prime}\in \mathcal{T}$
. Note that
$T^{\prime}\in \mathcal{T}$
. Note that
![]() ${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT^{\prime},T) =\mathop{\textrm{H}}\nolimits _i{\textrm{Hom}}(T^{\prime},T)=0$
for any
${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT^{\prime},T) =\mathop{\textrm{H}}\nolimits _i{\textrm{Hom}}(T^{\prime},T)=0$
for any
![]() $T^{\prime}\in \mathcal{T}$
. Thus, we say that
$T^{\prime}\in \mathcal{T}$
. Thus, we say that
![]() ${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\mathcal{A})}(\Sigma ^iT^{\prime},f)$
is an isomorphism for any
${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\mathcal{A})}(\Sigma ^iT^{\prime},f)$
is an isomorphism for any
![]() $i\in \mathbb{Z}$
. Let
$i\in \mathbb{Z}$
. Let
![]() $\mathop{\textrm{Cone}}\nolimits \!(f)$
be the mapping cone of
$\mathop{\textrm{Cone}}\nolimits \!(f)$
be the mapping cone of
![]() $f$
. It is easy to see that
$f$
. It is easy to see that
![]() $\mathop{\textrm{Cone}}\nolimits \!(f)$
is a fibrant by Corollary 4.6(3). From the triangle
$\mathop{\textrm{Cone}}\nolimits \!(f)$
is a fibrant by Corollary 4.6(3). From the triangle
![]() $T\stackrel{f}{\longrightarrow } X\to \mathop{\textrm{Cone}}\nolimits \!(f) \to \Sigma T$
in
$T\stackrel{f}{\longrightarrow } X\to \mathop{\textrm{Cone}}\nolimits \!(f) \to \Sigma T$
in
![]() $\mathop{\textrm{K}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
, we obtain
$\mathop{\textrm{K}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
, we obtain
![]() ${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT^{\prime},\mathop{\textrm{Cone}}\nolimits \!(f))=0$
for any
${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT^{\prime},\mathop{\textrm{Cone}}\nolimits \!(f))=0$
for any
![]() $T^{\prime}\in \mathcal{T}$
and any
$T^{\prime}\in \mathcal{T}$
and any
![]() $i\in \mathbb{Z}$
. Moreover, by Corollary 4.7,
$i\in \mathbb{Z}$
. Moreover, by Corollary 4.7,
![]() ${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT^{\prime},\mathop{\textrm{Cone}}\nolimits \!(f))=0$
for any
${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT^{\prime},\mathop{\textrm{Cone}}\nolimits \!(f))=0$
for any
![]() $T^{\prime}\in \mathcal{T}$
and any
$T^{\prime}\in \mathcal{T}$
and any
![]() $i\in \mathbb{Z}$
. Because
$i\in \mathbb{Z}$
. Because
![]() $\mathcal{T}$
satisfies the condition (3) of Definition 2.3,
$\mathcal{T}$
satisfies the condition (3) of Definition 2.3,
![]() $\mathop{\textrm{Cone}}\nolimits \!(f)=0$
in
$\mathop{\textrm{Cone}}\nolimits \!(f)=0$
in
![]() $\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
. Consequently,
$\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
. Consequently,
![]() $f$
becomes an isomorphism in
$f$
becomes an isomorphism in
![]() $\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
and
$\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
and
![]() $T$
satisfies (3).
$T$
satisfies (3).
Motivated by [Reference Bazzoni5, Theorem 3.5], we can assign a t-structure to a generalized tilting subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
.
Theorem 5.5.
Let
![]() $\mathcal{T}$
be a generalized tilting subcategory of
$\mathcal{T}$
be a generalized tilting subcategory of
![]() $\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
and
$\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C})$
and
![]() $k\in \mathbb{Z}$
. Then
$k\in \mathbb{Z}$
. Then
![]() $(\mathcal{D}^{\leqslant k}_{\mathcal{T}},\mathcal{D}^{\geqslant k}_{\mathcal{T}})$
forms a t-structure on the derived category
$(\mathcal{D}^{\leqslant k}_{\mathcal{T}},\mathcal{D}^{\geqslant k}_{\mathcal{T}})$
forms a t-structure on the derived category
![]() $\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
.
$\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
.
Proof. We will show that
![]() $(\mathcal{D}^{\leqslant 0}_{\mathcal{T}},\mathcal{D}^{\geqslant 0}_{\mathcal{T}})$
is a t-structure, since it is routine to check that the shifted pair
$(\mathcal{D}^{\leqslant 0}_{\mathcal{T}},\mathcal{D}^{\geqslant 0}_{\mathcal{T}})$
is a t-structure, since it is routine to check that the shifted pair
![]() $(\mathcal{D}^{\leqslant k}_{\mathcal{T}},\mathcal{D}^{\geqslant k}_{\mathcal{T}})$
is also a t-structure. The proof follows the pattern of that of [Reference Šťovíček31, Theorem 4.5], but in a dual manner. By the definition of
$(\mathcal{D}^{\leqslant k}_{\mathcal{T}},\mathcal{D}^{\geqslant k}_{\mathcal{T}})$
is also a t-structure. The proof follows the pattern of that of [Reference Šťovíček31, Theorem 4.5], but in a dual manner. By the definition of
![]() $\mathcal{D}^{\leqslant 0}_{\mathcal{T}}$
and
$\mathcal{D}^{\leqslant 0}_{\mathcal{T}}$
and
![]() $\mathcal{D}^{\geqslant 0}_{\mathcal{T}}$
, it is easy to verify that
$\mathcal{D}^{\geqslant 0}_{\mathcal{T}}$
, it is easy to verify that
![]() $\mathcal{D}^{\leqslant 0}_{\mathcal{T}}$
(resp.
$\mathcal{D}^{\leqslant 0}_{\mathcal{T}}$
(resp.
![]() $\mathcal{D}^{\geqslant 0}_{\mathcal{T}}$
) is closed under
$\mathcal{D}^{\geqslant 0}_{\mathcal{T}}$
) is closed under
![]() $\Sigma$
(resp.
$\Sigma$
(resp.
![]() $\Sigma ^{-1}$
). Thus, we only have to show the conditions (1) and (3) of Definition 5.1
$\Sigma ^{-1}$
). Thus, we only have to show the conditions (1) and (3) of Definition 5.1
In order to prove (1) of Definition 5.1, we assume that
![]() $X\in \mathcal{D}^{\leqslant 0}_{\mathcal{T}}$
and
$X\in \mathcal{D}^{\leqslant 0}_{\mathcal{T}}$
and
![]() $Y\in \mathcal{D}^{\geqslant 1}_{\mathcal{T}}$
. Let
$Y\in \mathcal{D}^{\geqslant 1}_{\mathcal{T}}$
. Let
![]() $X^{\prime}=\Sigma X$
and
$X^{\prime}=\Sigma X$
and
![]() $Y=\Sigma ^{-1}Y^{\prime}$
for some
$Y=\Sigma ^{-1}Y^{\prime}$
for some
![]() $Y^{\prime}\in \mathcal{D}^{\geqslant 0}_{\mathcal{T}}$
. Then
$Y^{\prime}\in \mathcal{D}^{\geqslant 0}_{\mathcal{T}}$
. Then
![]() ${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(X,Y)=0$
is equivalent to
${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(X,Y)=0$
is equivalent to
![]() ${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(X^{\prime},Y^{\prime})=0$
. In view of Proposition 5.4,
${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(X^{\prime},Y^{\prime})=0$
. In view of Proposition 5.4,
![]() $X^{\prime}$
has the form
$X^{\prime}$
has the form
![]() $\cdots \to X_2\to X_1\to 0\to \cdots$
with
$\cdots \to X_2\to X_1\to 0\to \cdots$
with
![]() $X_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
for every
$X_i\in \mathop{\textrm{Add}}\nolimits \!(\mathcal{T})$
for every
![]() $i\geqslant 1$
. For every
$i\geqslant 1$
. For every
![]() $n \geqslant 1$
, we shall denote by
$n \geqslant 1$
, we shall denote by
![]() $\tau _{\leqslant n}X^{\prime}$
the brutally truncated complex
$\tau _{\leqslant n}X^{\prime}$
the brutally truncated complex
![]() $\cdots 0\to X_n \to X_{n-1}\to \cdots \to X_1\to 0.$
As
$\cdots 0\to X_n \to X_{n-1}\to \cdots \to X_1\to 0.$
As
![]() ${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT^{\prime},Y^{\prime})=0$
for any
${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT^{\prime},Y^{\prime})=0$
for any
![]() $T^{\prime}\in \mathcal{T}$
and any
$T^{\prime}\in \mathcal{T}$
and any
![]() $i\gt 0$
, by induction on
$i\gt 0$
, by induction on
![]() $n$
, we know from the triangle
$n$
, we know from the triangle
![]() $\tau _{\leqslant n-1}X^{\prime}\to \tau _{\leqslant n}X^{\prime}\to \Sigma ^{n}X_n \to \Sigma (\tau _{\leqslant n-1}X^{\prime})$
that
$\tau _{\leqslant n-1}X^{\prime}\to \tau _{\leqslant n}X^{\prime}\to \Sigma ^{n}X_n \to \Sigma (\tau _{\leqslant n-1}X^{\prime})$
that
![]() ${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\tau _{\leqslant n}X^{\prime},Y^{\prime})=0={\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma (\tau _{\leqslant n}X^{\prime}),Y^{\prime})$
for all
${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\tau _{\leqslant n}X^{\prime},Y^{\prime})=0={\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma (\tau _{\leqslant n}X^{\prime}),Y^{\prime})$
for all
![]() $n\geqslant 1$
. Since
$n\geqslant 1$
. Since
![]() $X^{\prime}=\lim \limits _{\longrightarrow }\tau _{\leqslant n}X^{\prime}$
, by [Reference Miyachi27, Proposition 11.7], there is a triangle in
$X^{\prime}=\lim \limits _{\longrightarrow }\tau _{\leqslant n}X^{\prime}$
, by [Reference Miyachi27, Proposition 11.7], there is a triangle in
![]() $\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
of the form
$\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
of the form
Hence,
![]() ${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(X^{\prime},Y^{\prime})=0$
.
${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(X^{\prime},Y^{\prime})=0$
.
Now we will prove (3) of Definition 5.1. Let
![]() $X\in \mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
, in view of Corollary 4.6, we may assume that
$X\in \mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))$
, in view of Corollary 4.6, we may assume that
![]() $X$
has all the terms in
$X$
has all the terms in
![]() $\mathcal{T}^{\perp _{\infty }}$
. By Lemma 5.3, there is a chain map
$\mathcal{T}^{\perp _{\infty }}$
. By Lemma 5.3, there is a chain map
![]() $f\,:\, F\to X$
with
$f\,:\, F\to X$
with
![]() $F\in \mathop{\textrm{C}}\nolimits ^{[0,\infty ]}(\mathop{\textrm{Add}}\nolimits \!(\mathcal{T}))$
and
$F\in \mathop{\textrm{C}}\nolimits ^{[0,\infty ]}(\mathop{\textrm{Add}}\nolimits \!(\mathcal{T}))$
and
![]() ${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT,f)$
is an isomorphism for any
${\textrm{Hom}}_{\mathop{\textrm{K}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT,f)$
is an isomorphism for any
![]() $T\in \mathcal{T}$
and any
$T\in \mathcal{T}$
and any
![]() $i\geqslant 0$
. By Corollary 4.7, the same is true for
$i\geqslant 0$
. By Corollary 4.7, the same is true for
![]() ${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT,f)$
. Furthermore, it is straightforward to check that
${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT,f)$
. Furthermore, it is straightforward to check that
![]() $F\in \mathcal{D}^{\leqslant 0}_{\mathcal{T}}$
. Let
$F\in \mathcal{D}^{\leqslant 0}_{\mathcal{T}}$
. Let
![]() $\mathop{\textrm{Cone}}\nolimits \!(f)$
be the mapping cone of
$\mathop{\textrm{Cone}}\nolimits \!(f)$
be the mapping cone of
![]() $f$
, that is, we have a triangle
$f$
, that is, we have a triangle
Then necessarily
![]() ${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT,\mathop{\textrm{Cone}}\nolimits \!(f))=0$
for any
${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(\Sigma ^iT,\mathop{\textrm{Cone}}\nolimits \!(f))=0$
for any
![]() $i\gt 0$
. Indeed, if we apply
$i\gt 0$
. Indeed, if we apply
![]() ${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(T,\,\,\,\,)$
to (5.1), we get an exact sequence
${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(T,\,\,\,\,)$
to (5.1), we get an exact sequence
Now
![]() $f^{\prime}$
is an isomorphism and
$f^{\prime}$
is an isomorphism and
![]() ${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(T,\Sigma F)=0$
since
${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(T,\Sigma F)=0$
since
![]() $F\in \mathcal{D}^{\leqslant 0}_{\mathcal{T}}$
. Thus,
$F\in \mathcal{D}^{\leqslant 0}_{\mathcal{T}}$
. Thus,
![]() ${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(T,\mathop{\textrm{Cone}}\nolimits \!(f))=0$
. Hence,
${\textrm{Hom}}_{\mathop{\textrm{D}}\nolimits \!(\!\mathop{\textrm{Mod}}\nolimits \!(\mathcal{C}))}(T,\mathop{\textrm{Cone}}\nolimits \!(f))=0$
. Hence,
![]() $\mathop{\textrm{Cone}}\nolimits \!(f)\in \mathcal{D}^{\geqslant 1}_{\mathcal{T}}$
.
$\mathop{\textrm{Cone}}\nolimits \!(f)\in \mathcal{D}^{\geqslant 1}_{\mathcal{T}}$
.
Acknowledgements
The author thanks the referees for the useful suggestions, which improve the exposition of this paper. He thanks Alex Martsinkovsky for numerous inspiring discussions. This research was partially supported by NSFC (Grant No. 12061026) and NSF of Guangxi Province of China (Grant No. 2020GXNSFAA159120).