Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-26T02:47:35.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized fractions and Hughes' gradetheoretic analogue of the Cousin complex

Published online by Cambridge University Press:  18 May 2009

R. Y. Sharp  and
M. Yassi
R. Y. Sharp
Affiliation:
Department of Pure MathematicsUniversity of SheffieldHicks Building Sheffield S3 7RH
M. Yassi
Affiliation:
Department of Pure MathematicsUniversity of SheffieldHicks Building Sheffield S3 7RH
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a commutative Noetherian ring (with non-zero identity). The Cousin complex C(A) for A is described in [19, Section 2]: it is a complex of A-modules and A-homomorphisms

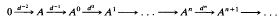
with the property that, for each n ∈ N0 (we use N0 to denote the set of non-negative integers),

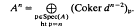
Cohen–Macaulay rings can be characterized in terms of the Cousin complex: A is a Cohen–Macaulay ring if and only if C(A) is exact [19, (4.7)]. Also, the Cousin complex provides a natural minimal injective resolution for a Gorenstein ring (see [19,(5.4)]).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 32 , Issue 2 , May 1990 , pp. 173 - 188
Copyright
Copyright © Glasgow Mathematical Journal Trust 1990

References

REFERENCES

1.Bijan-Zadeh, M. H., A common generalization of local cohomology theories, Glasgow Math. J. 21 (1980), 173–181.CrossRefGoogle Scholar
2.Bijan-Zadeh, M. H., Modules of generalized fractions and general local cohomology modules, Arch. Math. (Basel) 48 (1987), 58–62.CrossRefGoogle Scholar
3.de Chela, D. Flores, Flat dimensions of certain modules of generalized fractions, Quart J. Math. Oxford Ser. (2) 36 (1985), 413–423.CrossRefGoogle Scholar
4.Gibson, G. J., Modules of generalized fractions, matrices and determinantal maps, J. London Math. Soc. (2) 33 (1986), 245–252.CrossRefGoogle Scholar
5.Gibson, G. J., Direct limit systems and flat dimension of generalized fractions, Quart. J. Math. Oxford Ser. (2) 38 (1987), 313–319.CrossRefGoogle Scholar
6.Gibson, G. J. and O'Carroll, L., Direct limit systems, generalized fractions and complexes of Cousin type, J. Pure Appl. Algebra 54 (1988), 249–259.CrossRefGoogle Scholar
7.Grothendieck, A., Local cohomology, Lecture Notes in Mathematics 41 (Springer, 1967).Google Scholar
8.Hamieh, M. A. and Sharp, R. Y., Krull dimension and generalized fractions, Proc. Edinburgh Math. Soc. (2) 28 (1985), 349–353.CrossRefGoogle Scholar
9.Hamieh, M. A. and Zakeri, H., Denominator systems and modules of generalized fractions, J. London Math. Soc. (2) 33 (1986), 237–244.CrossRefGoogle Scholar
10.Hughes, K. R., A grade-theoretic analogue of the Cousin complex, Quaestiones Math. 9 (1986), 293–300.CrossRefGoogle Scholar
11.Lambek, J., Torsion theories, additive semantics, and rings of quotients, Lecture Notes in Mathematics 177 (Springer, 1971).CrossRefGoogle Scholar
12.Macdonald, I. G. and Sharp, R. Y., An elementary proof of the non-vanishing of certain local cohomology modules, Quart. J. Math. Oxford Ser. (2) 23 (1972), 197–204.CrossRefGoogle Scholar
13.Matsumura, H., Commutative ring theory (Cambridge University Press, 1986).Google Scholar
14.O'Carroll, L., On the generalized fractions of Sharp and Zakeri, J. London Math. Soc. (2) 28 (1983), 417–427.CrossRefGoogle Scholar
15.O'Carroll, L., Generalized fractions, determinantal maps, and top cohomology modules, J. Pure Appl. Algebra 32 (1984), 59–70.CrossRefGoogle Scholar
16.Northcott, D. G., An introduction to homological algebra (Cambridge University Press, 1960).CrossRefGoogle Scholar
17.Rees, D., The grade of an ideal or module, Proc. Cambridge Philos. Soc. 53 (1957), 28–42.CrossRefGoogle Scholar
18.Riley, A. M., Sharp, R. Y. and Zakeri, H., Cousin complexes and generalized fractions, Glasgow Math. J. 26 (1985), 51–67.CrossRefGoogle Scholar
19.Sharp, R. Y., The Cousin complex for a module over a commutative Noetherian ring, Math. Z. 112 (1969), 340–356.CrossRefGoogle Scholar
20.Sharp, R. Y., Local cohomology theory in commutative algebra, Quart. J. Math. Oxford Ser. (2) 21 (1970), 425–434.CrossRefGoogle Scholar
21.Sharp, R. Y., A Cousin complex characterization of balanced big Cohen-Macaulay modules, Quart. J. Math. Oxford Ser. (2) 33 (1982), 471–485.CrossRefGoogle Scholar
22.Sharp, R. Y. and Hamieh, M. A., Lengths of certain generalized fractions, J. Pure Appl. Algebra 38 (1985), 323–336.CrossRefGoogle Scholar
23.Sharp, R. Y. and Zakeri, H., Modules of generalized fractions, Mathematika 29 (1982), 32–41.CrossRefGoogle Scholar
24.Sharp, R. Y. and Zakeri, H., Local cohomology and modules of generalized fractions, Mathematika 29 (1982), 296–306.CrossRefGoogle Scholar
25.Sharp, R. Y. and Zakeri, H., Modules of generalized fractions and balanced big Cohen-Macaulay modules, Commutative algebra: Durham 1981, London Mathematical Society Lecture Notes 72 (Cambridge University Press, 1982), 61–82.Google Scholar
26.Sharp, R. Y. and Zakeri, H., Generalized fractions and the monomial conjecture, J. Algebra 92 (1985), 380–388.CrossRefGoogle Scholar
27.Sharp, R. Y. and Zakeri, H., Generalized fractions, Buchsbaum modules, and generalized Cohen-Macaulay modules, Math. Proc. Cambridge Philos. Soc. 98 (1985), 429–436.CrossRefGoogle Scholar
28.Zakeri, H., d-sequences, local cohomology modules and generalized analytic independence, Mathematika 33 (1986), 279–284.CrossRefGoogle Scholar