Article contents
Galois groups associated with CM-fields, skew-symmetric matrices and orthogonal matrices
Published online by Cambridge University Press: 18 May 2009
Extract
The main aims of this paper are to provide a device for constructing large families of complex-multiplication (CM) fields, and to examine the Galois groups of some related field extensions. We recall that an algebraic number field K (i.e. 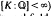 ) is called a CM-field if it is totally complex but is quadratic over some totally real field (see Section 1). CM fields are important in algebraic geomety, since the ring of endomorphisms of a simple abelian variety defined over an algebraic number field is either ℤ or a ℤ-order in a CM field. Moreover, CM fields figure prominently in classfield theory, since Shimura [15] has shown that “almost all” classfields over CM fields K can be generated by means of division points on abelian varieties admitting ℤ-orders in K as their endomorphism rings. Shimura's work can be regarded as a natural generalization of the classical method (due to Kronecker and H. Weber) of generating classfields of imaginary quadratic fields via division points on CM-elliptic curves.
) is called a CM-field if it is totally complex but is quadratic over some totally real field (see Section 1). CM fields are important in algebraic geomety, since the ring of endomorphisms of a simple abelian variety defined over an algebraic number field is either ℤ or a ℤ-order in a CM field. Moreover, CM fields figure prominently in classfield theory, since Shimura [15] has shown that “almost all” classfields over CM fields K can be generated by means of division points on abelian varieties admitting ℤ-orders in K as their endomorphism rings. Shimura's work can be regarded as a natural generalization of the classical method (due to Kronecker and H. Weber) of generating classfields of imaginary quadratic fields via division points on CM-elliptic curves.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1990
References
REFERENCES
- 2
- Cited by


