Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-12T02:45:32.234Z Has data issue: false hasContentIssue false
  • English
  • Français

Free products of two real cyclic matrix groups

Published online by Cambridge University Press:  18 May 2009

R. J. Evans
R. J. Evans
Affiliation:
University of Wisconsin, Madison, Wisconsin 53706, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We exhibit a large class K* of real 2 × 2 matrices of determinant ±1 such that, for nearly all A and B in K*, the group generated by A and B1 (the transpose of B) is the free product of the cyclic groups 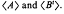It is shown that K* contains all matrices 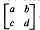of determinant ±1 with integer entries satisfying |b| > |a|, |c|, |d|. This gives a generalization of a theorem of Goldberg and Newman [2]. We also prove related results concerning the dominance of b and the discreteness of the free products .

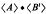Type
Research Article
Information
Glasgow Mathematical Journal , Volume 15 , Issue 2 , September 1974 , pp. 121 - 128
Copyright
Copyright © Glasgow Mathematical Journal Trust 1974

References

REFERENCES

1.Brenner, J., Quelques groupes libres de matrices, C. R. Acad. Sci. Paris 241 (1955), 1681–1691.Google Scholar
2.Goldberg, K. and Newman, M., Pairs of matrices of order two which generate free groups, Illinois J. Math. 1 (1957), 446–448.CrossRefGoogle Scholar
3.Knapp, A., Doubly generated Fuchsian groups, Michigan Math. J. 15 (1968), 289–304.CrossRefGoogle Scholar
4.Lyndon, R. and Ullman, J., Pairs of real 2-by-2 matrices that generate free products, Michigan Math. J. 15 (1968), 161–166.Google Scholar
5.Lyndon, R. and Ullman, J., Groups generated by two parabolic linear fractional transformations, Canadian J. Math. 21 (1969), 1388–1403.Google Scholar
6.Newman, M., Pairs of matrices generating discrete free groups and free products, Michigan Math. J. 15 (1968), 155–160.Google Scholar
7.Purzitsky, N., Two-generator discrete free products, Math. Z. 126 (1972), 209–223.CrossRefGoogle Scholar