Article contents
FREE ACTIONS OF SOME COMPACT GROUPS ON MILNOR MANIFOLDS
Published online by Cambridge University Press: 31 October 2018
Abstract
In this paper, we investigate free actions of some compact groups on cohomology real and complex Milnor manifolds. More precisely, we compute the mod 2 cohomology algebra of the orbit space of an arbitrary free ℤ2 and 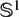 $\mathbb{S}^1$-action on a compact Hausdorff space with mod 2 cohomology algebra of a real or a complex Milnor manifold. As applications, we deduce some Borsuk–Ulam type results for equivariant maps between spheres and these spaces. For the complex case, we obtain a lower bound on the Schwarz genus, which further establishes the existence of coincidence points for maps to the Euclidean plane.
$\mathbb{S}^1$-action on a compact Hausdorff space with mod 2 cohomology algebra of a real or a complex Milnor manifold. As applications, we deduce some Borsuk–Ulam type results for equivariant maps between spheres and these spaces. For the complex case, we obtain a lower bound on the Schwarz genus, which further establishes the existence of coincidence points for maps to the Euclidean plane.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2018
References
REFERENCES
- 7
- Cited by


