Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-20T17:26:56.936Z Has data issue: false hasContentIssue false
  • English
  • Français

FRACTIONAL SCHRÖDINGER–POISSON SYSTEM WITH SINGULARITY: EXISTENCE, UNIQUENESS, AND ASYMPTOTIC BEHAVIOR

Part of: Miscellaneous topics - Partial differential equations Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  12 March 2020

SHENGBIN YU  and
JIANQING CHEN
SHENGBIN YU
Affiliation:
College of Mathematics and Informatics & FJKLMAA, Fujian Normal University, Qishan Campus, Fuzhou, Fujian350117, China Department of Basic Teaching and Research, Yango University, Fuzhou, Fujian350015, China, e-mail: [email protected]
JIANQING CHEN
Affiliation:
College of Mathematics and Informatics & FJKLMAA, Fujian Normal University, Qishan Campus, Fuzhou, Fujian350117, China, e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the following fractional Schrödinger–Poisson system with singularity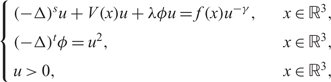

\begin{equation*} \left \{\begin{array}{lcl} ({-}\Delta)^s u+V(x)u+\lambda \phi u = f(x)u^{-\gamma}, &&\quad x\in\mathbb{R}^3,\\ ({-}\Delta)^t \phi = u^2, &&\quad x\in\mathbb{R}^3,\\ u>0,&&\quad x\in\mathbb{R}^3, \end{array}\right. \end{equation*}

where 0 < γ < 1, λ > 0 and 0 < s ≤ t < 1 with 4s + 2t > 3. Under certain assumptions on V and f, we show the existence, uniqueness, and monotonicity of positive solution uλ using the variational method. We also give a convergence property of uλ as λ → 0, when λ is regarded as a positive parameter.

MSC classification

Primary: 35J20: Variational methods for second-order elliptic equations
Secondary: 35R11: Fractional partial differential equations 35B09: Positive solutions 35B40: Asymptotic behavior of solutions
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 1 , January 2021 , pp. 179 - 192
Copyright
© The Author(s) 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adimurthi, J. Giacomoni and Santra, S., Positive solutions to a fractional equation with singular nonlinearity, J. Differ. Equ. 265 (2018), 1191–1226.CrossRefGoogle Scholar
Applebaum, D., Lévy processes-from probability to finance and quantum groups, Not. Amer. Math. Soc. 51 (2004), 1336–1347.Google Scholar
Di Nezza, E., Palatucci, G. and Valdinoci, E., Hitchhiker’s guide to the fractioal Sobolev spaces, Bull. Sci. Math. 136 (2012), 521–573.Google Scholar
Fang, Y., Existence, uniqueness of positive solution to a fractional Laplacians with singular nonlinearity, preprint (2014). http://arxiv.org/pdf/1403.3149.pdf.Google Scholar
Fiscella, A., A fractional Kirchhoff problem involving a singular term and a critical nonlinearity, Adv. Nonlinear Anal. 8 (2019), 645–660.Google Scholar
Fiscella, A. and Mishra, P., The Nehari manifold for fractional Kirchhoff problems involving singular and critical terms, Nonlinear Anal. 186 (2019), 6–32.CrossRefGoogle Scholar
Gao, Z., Tang, X. and Chen, S., Ground state solutions for a class of nonlinear fractional Schrödinger-Poisson systems with super-quadratic nonlinearity, Chaos Solitons Fractals 105 (2017), 189–194.CrossRefGoogle Scholar
Ghanmi, A. and Saoudi, K., The Nehari manifold for a singular elliptic equation involving the fractional Laplace operator, Fract. Differ. Calculus 6 (2016), 201–217.CrossRefGoogle Scholar
Giacomoni, J., Mukherjee, T. and Sreenadh, K., Positive solutions of fractional elliptic equation with critical and singular nonlinearity, Adv. Nonlinear Anal. 6 (2017), 327–354.CrossRefGoogle Scholar
Giacomoni, J., Mukherjee, T. and Sreenadh, K., A global multiplicity result for a very singular critical nonlocal equation, Topol. Methods Nonlinear Anal. (2019). DOI: 10.12775/TMNA.2019.049.CrossRefGoogle Scholar
Giacomoni, J., Mukherjee, T. and Sreenadh, K., Existence of three positive solutions for a nonlocal singular Dirichlet boundary problem, Adv. Nonlinear Stud. 19 (2019), 333–352.CrossRefGoogle Scholar
Goncalves, J., Melo, A. and Santos, C., On existence of L ∞-ground states for singular elliptic equations in the presence of a strongly nonlinear term, Adv. Nonlinear Stud. 7 (2007), 475–490.CrossRefGoogle Scholar
Goyal, S., Fractional Hardy-Sobolev operator with sign-changing and singular nonlinearity, Appl. Anal. (2019). DOI: 10.1080/00036811.2019.1585535.Google Scholar
Gu, G., Tang, X. and Zhang, Y., Existence of positive solutions for a class of critical fractional Schrödinger-Poisson system with potential vanishing at infinity, Appl. Math. Lett. 99 (2020), 105984.CrossRefGoogle Scholar
Guo, L., Sign-changing solutions for fractional Schrödinger-Poisson system in $\mathbb{R}^3$ , Appl. Anal. 98 (2019), 2085–2104.CrossRefGoogle Scholar
He, Y. and Jing, L., Existence and multiplicity of non-trivial solutions for the fractional Schrödinger-Poisson system with superlinear terms, Bound. Value Probl. 2019 (2019), 4.Google Scholar
Lei, C. and Liao, J., Multiple positive solutions for Kirchhoff type problems with singularity and asymptotically linear nonlinearities, Appl. Math. Lett. 94 (2019), 279–285.CrossRefGoogle Scholar
Lei, C. and Liao, J., Multiple positive solutions for Schrödinger-Poisson system involving singularity and critical exponent, Math. Meth. Appl. Sci. 42 (2019), 2417–2430.CrossRefGoogle Scholar
Lei, C., Suo, H. and Chu, C., Multiple positive solutions for a Schrödinger-Newton system with singularity and critical growth, Electron. J. Differ. Equ. 86 (2018), 1–15.Google Scholar
Li, K., Existence of non-trivial solutions for nonlinear fractional Schrödinger-Poisson equations, Appl. Math. Lett. 72 (2017), 1–9.CrossRefGoogle Scholar
Li, W., Rădulescu, V. and Zhang, B., Infinitely many solutions for fractional Kirchhoff-Schrödinger-Poisson systems, J. Math. Phys. 60 (2019), 011506. DOI: 10.1063/1.5019677.Google Scholar
Li, F., Song, Z. and Zhang, Q., Existence and uniqueness results for Kirchhoff-Schrödinger-Poisson system with general singularity, Appl. Anal. 96 (2017), 2906–2916.Google Scholar
Mu, M. and Lu, H., Existence and multiplicity of positive solutions for Schrödinger-Kirchhoff-Poisson system with singularity, J. Funct. Spaces 2017 (2017), 5985962.Google Scholar
Mukherjee, T. and Sreenadh, K., Fractional elliptic equations with critical growth and singular nonlinearities, Electron. J. Differ. Equ. 54 (2016), 1–23.Google Scholar
Mukherjee, T. and Sreenadh, K., Positive solutions for nonlinear Choquard equation with singular nonlinearity, Complex Var. Elliptic Equ. 62 (2017), 1044–1071.CrossRefGoogle Scholar
Saoudi, K., A critical fractional elliptic equation with singular nonlinearities, Fract. Calc. Appl. Anal. 20 (2017), 1507–1530.CrossRefGoogle Scholar
Sun, Y., Compatibility phenomena in singular problems, Proc. Roy. Soc. Edinburgh Sect. A 143 (2013), 1321–1330.Google Scholar
Sun, Y. and Li, S., Structure of ground state solutions of singular semilinear elliptic equations, Nonlinear Anal. 55 (2003), 399–417.Google Scholar
Teng, K., Existence of ground state solutions for the nonlinear fractional Schrödinger-Poisson system with critical Sobolev exponent, J. Differ. Equ. 261 (2016), 3061–3106.CrossRefGoogle Scholar
Teng, K. and Agarwal, R., Existence and concentration of positive ground state solutions for nonlinear fractional Schrödinger-Poisson system with critical growth, Math. Meth. Appl. Sci. 41 (2018), 8258–8293.CrossRefGoogle Scholar
Wang, L., Multiple positive solutions for a kind of singular Schrödinger-Poisson system, Appl. Anal. (2018). DOI: 10.1080/00036811.2018.1491035.Google Scholar
Wang, X. and Zhang, L., Existence and multiplicity of weak positive solutions to a class of fractional Laplacian with a singular nonlinearity, Results Math. 74 (2019), 81.CrossRefGoogle Scholar
Xiang, M. and Wang, F., Fractional Schrödinger-Poisson-Kirchhoff type systems involving critical nonlinearities, Nonlinear Anal. 164 (2017), 1–26.CrossRefGoogle Scholar
Ye, C. and Teng, K., Ground state and sign-changing solutions for fractional Schrödinger-Poisson system with critical growth, Complex Var. Elliptic Equ. (2019). DOI: 10.1080/17476933.2019.1652278.Google Scholar
Yu, S. and Chen, J., Uniqueness and asymptotical behavior of solutions to a Choquard equation with singularity, Appl. Math. Lett. 102 (2020), 106099.CrossRefGoogle Scholar
Yu, Y., Zhao, F. and Zhao, L., Positive and sign-changing least energy solutions for a fractional Schrödinger-Poisson system with critical exponent, Appl. Anal. (2018). DOI: 10.1080/00036811.2018.1557325.Google Scholar
Yu, Y., Zhao, F. and Zhao, L., The existence and multiplicity of solutions of a fractional Schrödinger-Poisson system with critical growth, Sci. China Math. 61 (2018), 1039–1062.CrossRefGoogle Scholar
Zhang, Q., Existence, uniqueness and multiplicity of positive solutions for Schrödinger-Poisson system with singularity, J. Math. Anal. Appl. 437 (2016), 160–180.CrossRefGoogle Scholar
Zhang, Q., Multiple positive solutions for Kirchhoff-Schrödinger-Poisson system with general singularity, Bound. Value Probl. 2017 (2017), 127.CrossRefGoogle Scholar
Zhang, J., J. do Ó and M. Squassina, Fractional Schrödinger-Poisson systems with a general subcritical or critical nonlinearity, Adv. Nonlinear Stud. 16 (2016), 15–30.Google Scholar