Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-12-01T04:53:51.508Z Has data issue: false hasContentIssue false
  • English
  • Français

The Fourier transform of vector-valued functions

Published online by Cambridge University Press:  18 May 2009

Susumu Okada
Susumu Okada
Affiliation:
Department of Mathematical Sciences, San Diego State University, San Diego, CA 92182-0314, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For each natural number n, let un(x)=(1—cos nx)/πnx2(xɛℝ). It is well–known that a bounded continuous function f on the real line ℝ is the Fourier transform of an integrable function on ℝ if and only if the functions Φn(f) (n= 1, 2,…), defined by

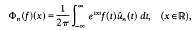
form a Cauchy sequence in the space L1(ℝ) (cf. [2]). Such a characterization, which can be extended to functions defined on a locally compact Abelian group more general than ℝ, is based on the fact that the space L1(ℝ) is complete with respect to convergence in mean.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 26 , Issue 2 , July 1985 , pp. 181 - 186
Copyright
Copyright © Glasgow Mathematical Journal Trust 1985

References

REFERENCES

1.Bukovská, Z., Characterization of Fourier transforms of vector valued functions and measures, Mat. Časopis Sloven Akad. Vied., 20 (1970), 109–114.Google Scholar
2.Cramér, H., On the representations of a function by certain Fourier integrals, Trans. Amer. Math. Soc. 49 (1939), 191–201.CrossRefGoogle Scholar
3.Diestel, J. and Uhl, J. J. Jr, Vector measures, Math. Surveys, 15, (Amer. Math. Soc., Providence, 1977).CrossRefGoogle Scholar
4.Hewitt, E. and Ross, K. A., Abstract harmonic analysis II, Grundlehren, 152, (Springer-Verlag, 1970).Google Scholar
5.Kluvánek, I., Characterization of Fourier-Stieltjes transforms of vector and operator-valued measures, Czechoslovak Math. J., 17 (92) (1967), 261–277.CrossRefGoogle Scholar
6.Kluvánek, I., Fourier transforms of vector-valued functions and measures, Studia Math., 37 (1970), 1–12.CrossRefGoogle Scholar
7.Okada, S., Integration of vector-valued functions, in Measure theory and its applications, Lecture Notes in Mathematics No. 1033 (Springer-Verlag, 1983), 247–257.CrossRefGoogle Scholar
8.Pettis, B. J., On integration in vector spaces, Trans. Amer. Math. Soc., 44 (1938), 277–304.CrossRefGoogle Scholar
9.Rudin, W., Fourier analysis on groups, (Interscience, New York, 1960).Google Scholar
10.Simon, A. B., Cesáro summability on groups: characterization and inversion of Fourier transforms, in Function algebra (Scott, Foresman and Company, Glenview, 1966), 208–215.Google Scholar
11.Wong, J. S. W., On a characterization of Fourier transforms, Monatsh. Math., 70 (1966), 74–80.CrossRefGoogle Scholar