Article contents
FINITENESS OF TOPOLOGICAL ENTROPY FOR LOCALLY COMPACT ABELIAN GROUPS
Published online by Cambridge University Press: 26 February 2020
Abstract
We study the locally compact abelian groups in the class 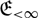 ${\mathfrak E_{ \lt \infty }}$
, that is, having only continuous endomorphisms of finite topological entropy, and in its subclass
${\mathfrak E_{ \lt \infty }}$
, that is, having only continuous endomorphisms of finite topological entropy, and in its subclass 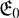 $\mathfrak E_0$
, that is, having all continuous endomorphisms with vanishing topological entropy. We discuss the reduction of the problem to the case of periodic locally compact abelian groups, and then to locally compact abelian p-groups. We show that locally compact abelian p-groups of finite rank belong to
$\mathfrak E_0$
, that is, having all continuous endomorphisms with vanishing topological entropy. We discuss the reduction of the problem to the case of periodic locally compact abelian groups, and then to locally compact abelian p-groups. We show that locally compact abelian p-groups of finite rank belong to 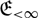 ${\mathfrak E_{ \lt \infty }}$
, and that those of them that belong to
${\mathfrak E_{ \lt \infty }}$
, and that those of them that belong to 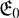 $\mathfrak E_0$
are precisely the ones with discrete maximal divisible subgroup. Furthermore, the topological entropy of endomorphisms of locally compact abelian p-groups of finite rank coincides with the logarithm of their scale. The backbone of the paper is the Addition Theorem for continuous endomorphisms of locally compact abelian groups. Various versions of the Addition Theorem are established in the paper and used in the proofs of the main results, but its validity in the general case remains an open problem.
$\mathfrak E_0$
are precisely the ones with discrete maximal divisible subgroup. Furthermore, the topological entropy of endomorphisms of locally compact abelian p-groups of finite rank coincides with the logarithm of their scale. The backbone of the paper is the Addition Theorem for continuous endomorphisms of locally compact abelian groups. Various versions of the Addition Theorem are established in the paper and used in the proofs of the main results, but its validity in the general case remains an open problem.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
References
REFERENCES
- 2
- Cited by


