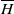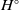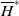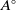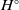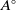1. Introduction
1.1 Background
This is the second in a series of papers about affine commutative-by-finite Hopf algebras and their duals, the first in the series being [Reference Brown and Couto3]. In that paper, we defined a Hopf algebra H over the algebraically closed field k to be affine commutative-by-finite if H is a finitely generated module over a normal commutative finitely generated Hopf subalgebra A. (To say that A is normal in H means that it is closed under the adjoint actions of H on A, recalled at the start of Section 2.1.) Let
![]() $A^+$
denote the augmentation ideal of A. Normality of A ensures that
$A^+$
denote the augmentation ideal of A. Normality of A ensures that
![]() $A^+H$
is a Hopf ideal of H, so that
$A^+H$
is a Hopf ideal of H, so that
![]() $\overline{H} \;:\!=\; H/A^+ H$
is a finite dimensional quotient Hopf algebra of H, and it is natural to view H as an extension of A by
$\overline{H} \;:\!=\; H/A^+ H$
is a finite dimensional quotient Hopf algebra of H, and it is natural to view H as an extension of A by
![]() $\overline{H}$
.
$\overline{H}$
.
Our aim in this paper is to obtain, for an affine commutative-by-finite Hopf algebra H, a description of the finite dual
![]() $H^{\circ}$
of H which generalises the classical description valid when
$H^{\circ}$
of H which generalises the classical description valid when
![]() $H = A$
given by the Cartier–Gabriel–Kostant structure theorem [Reference Montgomery26, Corollary 5.6.4, Theorem 5.6.5]. Recall that in that case, assuming that k has characteristic 0,
$H = A$
given by the Cartier–Gabriel–Kostant structure theorem [Reference Montgomery26, Corollary 5.6.4, Theorem 5.6.5]. Recall that in that case, assuming that k has characteristic 0,
![]() $A^{\circ}$
is a smash product
$A^{\circ}$
is a smash product
![]() $U(\mathfrak{g}) \sharp kG$
, where A is the algebra of polynomial functions
$U(\mathfrak{g}) \sharp kG$
, where A is the algebra of polynomial functions
![]() $\mathcal{O}(G)$
of the affine algebraic group G,
$\mathcal{O}(G)$
of the affine algebraic group G,
![]() $U(\mathfrak{g})$
is the enveloping algebra of its Lie algebra
$U(\mathfrak{g})$
is the enveloping algebra of its Lie algebra
![]() $\mathfrak{g}$
and kG is the group algebra of G. The description we obtain combines (generalisations of) these ingredients with the dual
$\mathfrak{g}$
and kG is the group algebra of G. The description we obtain combines (generalisations of) these ingredients with the dual
![]() $\overline{H}^{\ast}$
of
$\overline{H}^{\ast}$
of
![]() $\overline{H}$
. It comes closest to replicating the classical cocommutative picture when H satisfies two additional hypotheses. Currently, we know of no examples where these hypotheses fail to hold. We briefly explain the additonal hypotheses in Section 1.2, then state the main theorem in Section 1.3.
$\overline{H}$
. It comes closest to replicating the classical cocommutative picture when H satisfies two additional hypotheses. Currently, we know of no examples where these hypotheses fail to hold. We briefly explain the additonal hypotheses in Section 1.2, then state the main theorem in Section 1.3.
1.2 Coideal splitting and orbital semisimplicity
Let H and its Hopf subalgebra A satisfy the hypotheses of Section 1.1, and assume that A is semiprime or central, or that H is pointed. It is known, as we will recall in Theorem 2.2, that A is a direct summand of H as right A-modules, say
Our first additional hypothesis is:
To explain the second hypothesis, note first that the left adjoint action of H on A factors through
![]() $\overline{H}$
, so that for each maximal ideal
$\overline{H}$
, so that for each maximal ideal
![]() $\mathfrak{m}$
of A we can define
$\mathfrak{m}$
of A we can define
![]() $\mathfrak{m}^{(\overline{H})}$
to be the unique largest
$\mathfrak{m}^{(\overline{H})}$
to be the unique largest
![]() $\overline{H}$
-invariant ideal of A contained in
$\overline{H}$
-invariant ideal of A contained in
![]() $\mathfrak{m}$
. By work of Skryabin [Reference Skryabin33], which we recall in Section 5.1,
$\mathfrak{m}$
. By work of Skryabin [Reference Skryabin33], which we recall in Section 5.1,
![]() $A/\mathfrak{m}^{(\overline{H})}$
is a finite dimensional algebra. The second hypothesis is:
$A/\mathfrak{m}^{(\overline{H})}$
is a finite dimensional algebra. The second hypothesis is:
1.3 Main theorem
Here is the main result stated here in the simplest case, namely when k has characteristic 0; the full result is Theorem 6.1. The symbol
![]() $R\#T$
is used to denote the smash product of the k-algebra R by the Hopf algebra T, see [Reference Montgomery26, Definition 4.1.3].
$R\#T$
is used to denote the smash product of the k-algebra R by the Hopf algebra T, see [Reference Montgomery26, Definition 4.1.3].
Theorem 1.1. Let k have characteristic 0 and let H be an affine commutative-by-finite Hopf k-algebra, finite over the normal commutative Hopf subalgebra A. (So
![]() $A = \mathcal{O}(G_H)$
for an affine algebraic k-group
$A = \mathcal{O}(G_H)$
for an affine algebraic k-group
![]() $G_H$
with Lie algebra
$G_H$
with Lie algebra
![]() $\mathfrak{g}$
.) Assume that
$\mathfrak{g}$
.) Assume that
![]() $A \subseteq H$
satisfies (CoSplit) and (OrbSemi). Denote the finite dual of H by
$A \subseteq H$
satisfies (CoSplit) and (OrbSemi). Denote the finite dual of H by
![]() $H^{\circ}$
and recall that
$H^{\circ}$
and recall that
![]() $\overline{H}$
denotes the finite dimensional Hopf algebra
$\overline{H}$
denotes the finite dimensional Hopf algebra
![]() $H/A^+ H$
.
$H/A^+ H$
.
-
(1) As a vector space,
 $H^\circ$
decomposes as
$H^\circ$
decomposes as
 $U(\mathfrak{g}) \otimes \overline{H}^{\ast} \otimes kG_H$
; as an algebra it decomposes as a smash product (1.2)
$U(\mathfrak{g}) \otimes \overline{H}^{\ast} \otimes kG_H$
; as an algebra it decomposes as a smash product (1.2) \begin{equation}H^\circ \;\cong \; \overline{H}^{\ast} \#\, A^\circ \;\cong \; (\overline{H}^{\ast} \# \,U(\mathfrak{g}))\# kG_H.\end{equation}
\begin{equation}H^\circ \;\cong \; \overline{H}^{\ast} \#\, A^\circ \;\cong \; (\overline{H}^{\ast} \# \,U(\mathfrak{g}))\# kG_H.\end{equation}
-
(2)
 $H^\circ$
contains three distinguished Hopf subalgebras, namely
$H^\circ$
contains three distinguished Hopf subalgebras, namely
 $\overline{H}^{\ast}$
, a differential smash product (1.3)and a skew group algebra
$\overline{H}^{\ast}$
, a differential smash product (1.3)and a skew group algebra \begin{equation}W(H^\circ) \; \cong \;\overline{H}^{\ast} \#\, U(\mathfrak{g}),\end{equation}
(1.4)
\begin{equation}W(H^\circ) \; \cong \;\overline{H}^{\ast} \#\, U(\mathfrak{g}),\end{equation}
(1.4) \begin{equation}\widehat{kG_{H\;\,}} \cong \; \overline{H}^{\ast} \#\, kG_H.\end{equation}
\begin{equation}\widehat{kG_{H\;\,}} \cong \; \overline{H}^{\ast} \#\, kG_H.\end{equation}
-
(3) Suppose in addition that
 $\overline{H}$
is semisimple. Then the action of
$\overline{H}$
is semisimple. Then the action of
 $U(\mathfrak{g})$
on
$U(\mathfrak{g})$
on
 $\overline{H}^{\ast}$
is inner, so that (1.5)a skew group algebra with coefficient ring the Hopf subalgebra
$\overline{H}^{\ast}$
is inner, so that (1.5)a skew group algebra with coefficient ring the Hopf subalgebra \begin{equation} H^{\circ} \; \cong \; (\overline{H}^{\ast} \otimes U(\mathfrak{g})) \# kG_H,\end{equation}
\begin{equation} H^{\circ} \; \cong \; (\overline{H}^{\ast} \otimes U(\mathfrak{g})) \# kG_H,\end{equation}
 $W(H^{\circ})$
.
$W(H^{\circ})$
.
We currently know no counterexample to the possibility that, given any affine commutative-by-finite Hopf algebra H, there is a choice of normal commutative Hopf subalgebra
![]() $A \subseteq H$
which satisfies
$A \subseteq H$
which satisfies
![]() $(\mathbf{{CoSplit}})$
and
$(\mathbf{{CoSplit}})$
and
![]() $(\mathbf{{OrbSemi}})$
. This is recorded as Question 6.3.
$(\mathbf{{OrbSemi}})$
. This is recorded as Question 6.3.
Versions of some of the results in this paper appeared in the PhD theses of the second and third authors, [Reference Couto11] and [Reference Jahn19]. Since both these theses are publicly available online, some detailed calculations from them are not repeated here; full references are given where this occurs.
The preprint [Reference Li and Liu22], which appeared while the present paper was being written, contains presentations by generators and relations of the finite duals
![]() $H^{\circ}$
of the affine prime regular Hopf algebras H of Gel’fand–Kirillov dimension one (all of which are commutative-by-finite). The results of [Reference Li and Liu22] and the present paper are largely complementary, the only overlap being with Section 7.5 of this paper, where the implications of Theorem 6.1 for prime regular affine Hopf algebras of GK-dimension one are examined.
$H^{\circ}$
of the affine prime regular Hopf algebras H of Gel’fand–Kirillov dimension one (all of which are commutative-by-finite). The results of [Reference Li and Liu22] and the present paper are largely complementary, the only overlap being with Section 7.5 of this paper, where the implications of Theorem 6.1 for prime regular affine Hopf algebras of GK-dimension one are examined.
1.4 Layout of the paper
The final Section 7 of the paper reviews a number of families of affine commutative-by-finite Hopf algebras. We discuss there the validity of the hypotheses of Theorem 6.1 for each family, and the consequences for the structure of the Hopf dual for the algebras in each family. The reader may find it helpful to review some of these examples in tandem with the rest of the paper.
There is a brief review of the properties of affine commutative-by-finite Hopf algebras H in Section 2. Section 3 is devoted to the proof of our first key result, Theorem 3.2, which obtains sufficient conditions for H to decompose as a crossed or smash product of
![]() $\overline{H}^{\ast}$
by
$\overline{H}^{\ast}$
by
![]() $A^{\circ}$
. Sections 4 and 5 are concerned, respectively, with the two Hopf subalgebras
$A^{\circ}$
. Sections 4 and 5 are concerned, respectively, with the two Hopf subalgebras
![]() $W(H^{\circ})$
and
$W(H^{\circ})$
and
![]() $\widehat{kG_H}$
of
$\widehat{kG_H}$
of
![]() $H^{\circ}$
which feature in Theorem 1.1(2), and which are, respectively, generalisations from the commutative case of
$H^{\circ}$
which feature in Theorem 1.1(2), and which are, respectively, generalisations from the commutative case of
![]() $U(\mathfrak{g})$
(in characteristic 0) and
$U(\mathfrak{g})$
(in characteristic 0) and
![]() $kG_H$
. It is in analysing the structure of
$kG_H$
. It is in analysing the structure of
![]() $\widehat{kG_H}$
that the hypothesis
$\widehat{kG_H}$
that the hypothesis
![]() $(\mathbf{{OrbSemi}})$
comes into play—this is introduced in Section 5.2. The very brief Section 6 contains the full statement of Theorem 6.1 and its deduction from the results of Sections 3–5.
$(\mathbf{{OrbSemi}})$
comes into play—this is introduced in Section 5.2. The very brief Section 6 contains the full statement of Theorem 6.1 and its deduction from the results of Sections 3–5.
1.5 Notation
Throughout this paper, k will denote an algebraically closed field, all vector spaces are over k unless stated otherwise, and all unadorned tensor products are over k. The Gelfand–Kirillov dimension of an algebra R will be denoted by
![]() ${\textrm{GK dim}}\;R$
; see [Reference Krause and Lenagan20] for details. For a Hopf algebra H, we use the usual notation of
${\textrm{GK dim}}\;R$
; see [Reference Krause and Lenagan20] for details. For a Hopf algebra H, we use the usual notation of
![]() $\Delta,\epsilon$
for the coalgebra structure, with
$\Delta,\epsilon$
for the coalgebra structure, with
![]() $\Delta(h)=\sum h_1\otimes h_2$
for
$\Delta(h)=\sum h_1\otimes h_2$
for
![]() $h \in H$
, and we use S to denote its antipode. The augmentation ideal
$h \in H$
, and we use S to denote its antipode. The augmentation ideal
![]() $\textrm{ker }\epsilon$
of a Hopf algebra H will always be denoted by
$\textrm{ker }\epsilon$
of a Hopf algebra H will always be denoted by
![]() $H^+$
. Further notation will be introduced in Section 2.2.
$H^+$
. Further notation will be introduced in Section 2.2.
2. Commutative-by-finite Hopf algebras
In this section, we briefly recall the most basic properties of affine commutative-by-finite Hopf algebras. At the same time notation will be fixed which will remain in force throughout the paper. Full details of the results stated here can be found in [Reference Brown and Couto3].
2.1 Definition and basic properties
Recall [Reference Montgomery26, Section 3.4] that a subalgebra K of a Hopf algebra H is normal if it is invariant under the left and right adjoint actions of H; that is, for all
![]() $k\in K$
and
$k\in K$
and
![]() $h\in H$
,
$h\in H$
,
The following class of Hopf algebras will be the focus of this paper.
Definition 2.1. A Hopf k-algebra H is affine commutative-by-finite if it is a finite (left or right) module over a commutative normal Hopf subalgebra A which is finitely generated as a k-algebra.
For full proofs and references for the following see [Reference Brown and Couto3, Section 2].
Theorem 2.2. Let H be an affine commutative-by-finite Hopf algebra, finite over the normal commutative Hopf subalgebra A with augmentation ideal
![]() $A^+$
.
$A^+$
.
-
(1) A and H are Noetherian k-algebras.
-
(2)
 $A^+ H = HA^+$
is a Hopf ideal of H, and is a finite dimensional quotient Hopf algebra of H. We denote the Hopf algebra surjection by
$A^+ H = HA^+$
is a Hopf ideal of H, and is a finite dimensional quotient Hopf algebra of H. We denote the Hopf algebra surjection by \begin{equation*} \overline{H} \; :\!=\; H/A^+ H \end{equation*}
\begin{equation*} \overline{H} \; :\!=\; H/A^+ H \end{equation*}
 $\pi\;:\;H \longrightarrow \overline{H}$
.
$\pi\;:\;H \longrightarrow \overline{H}$
.
-
(3) The left adjoint action of H on A factors through
 $\overline{H}$
, so that A is a left
$\overline{H}$
, so that A is a left
 $\overline{H}$
-module algebra.
$\overline{H}$
-module algebra. -
(4) The antipode S of H is bijective.
-
(5) H is a finite module over its centre Z(H), which is affine.
-
(6)
 $ {\textrm{GK dim}}\;H = {\textrm{GK dim}}\;A < \infty.$
$ {\textrm{GK dim}}\;H = {\textrm{GK dim}}\;A < \infty.$
Assume for (7)–(10) that A is semiprime or central, or that H is pointed.
-
(7) H is a finitely generated projective generator as left and right A-module.
-
(8) A is a left (resp. right) A-module direct summand of H.
-
(9)
 $A\subseteq H$
is a faithfully flat
$A\subseteq H$
is a faithfully flat
 $\overline{H}$
-Galois extension.
$\overline{H}$
-Galois extension. -
(10) A equals the right and the left
 $\overline{H}$
-coinvariants of the
$\overline{H}$
-coinvariants of the
 $\overline{H}$
-comodule H; that is,
$\overline{H}$
-comodule H; that is,  \begin{equation*} H^{\textrm{co }\pi} \; = \; ^{\textrm{co }\pi}H \; = \; A.\end{equation*}
\begin{equation*} H^{\textrm{co }\pi} \; = \; ^{\textrm{co }\pi}H \; = \; A.\end{equation*}
Remark 2.3. Keep the notation and hypotheses of Theorem 2.2.
-
(1) (Radford [Reference Radford27]) In general, H is not a free A-module. For example, let
 $H=\mathcal{O}(SL_2(k))$
. This commutative Hopf algebra is a finite module over the Hopf subalgebra A generated by the monomials of even degree, but it is not a free A-module.
$H=\mathcal{O}(SL_2(k))$
. This commutative Hopf algebra is a finite module over the Hopf subalgebra A generated by the monomials of even degree, but it is not a free A-module. -
(2) An important setting where H is A-free is when H decomposes as a crossed product
 $H = A \#_{\sigma} \overline{H}$
. By a celebrated result of Doi and Takeuchi [Reference Doi and Takeuchi14], this happens if and only if there is a cleaving map
$H = A \#_{\sigma} \overline{H}$
. By a celebrated result of Doi and Takeuchi [Reference Doi and Takeuchi14], this happens if and only if there is a cleaving map
 $\gamma:\overline{H} \longrightarrow H$
- that is,
$\gamma:\overline{H} \longrightarrow H$
- that is,
 $\gamma$
is a convolution invertible right
$\gamma$
is a convolution invertible right
 $\overline{H}$
-comodule map. Moreover, given that the extension is
$\overline{H}$
-comodule map. Moreover, given that the extension is
 $\overline{H}$
-Galois by Theorem 2.2(4), such a cleaving map exists if and only if
$\overline{H}$
-Galois by Theorem 2.2(4), such a cleaving map exists if and only if
 $A \subseteq H$
has the normal basis property. For details, see [Reference Montgomery26, Propositions 7.2.3, 7.2.7, Theorem 8.2.4]. Such a decomposition of H is guaranteed when the coradical of H is contained in AG(H), by [Reference Schneider30, Corollary 4.3].
$A \subseteq H$
has the normal basis property. For details, see [Reference Montgomery26, Propositions 7.2.3, 7.2.7, Theorem 8.2.4]. Such a decomposition of H is guaranteed when the coradical of H is contained in AG(H), by [Reference Schneider30, Corollary 4.3]. -
(3) Since Theorem 2.2(4) follows from [Reference Skryabin32, Corollary 2], which is valid for all Noetherian Hopf algebras satisfying a PI, in Definition 2.1 it is enough to require that A is normal on one side only; see [Reference Brown and Couto3, Lemma 4.10(1)].
-
(4) In seeking to apply Theorem 2.2(7)–(10) one can often reduce to the case where A is semiprime. For recall that A is always semiprime when k has characteristic 0 [Reference Waterhouse37, 11.6]. Moreover in characteristic
 $p > 0$
one can usually reach this setting by replacing A by its image under a suitable power of the Frobenius map; we leave the details to the interested reader.
$p > 0$
one can usually reach this setting by replacing A by its image under a suitable power of the Frobenius map; we leave the details to the interested reader.
2.2 Further notation
For brevity we shall henceforth record the set-up of Theorem 2.2, including
![]() $\overline{H}$
and the map
$\overline{H}$
and the map
![]() $\pi$
, as
$\pi$
, as
The nilrdical N(A) of the commutative affine Hopf k-algebra A is a Hopf ideal by [Reference Brown and Couto3, Lemma 5.2(1)]. There is thus an affine algebraic k-group
![]() $G_H$
such that
$G_H$
such that
![]() $A/N(A) \cong \mathcal{O}(G_H)$
[Reference Waterhouse37, 11.7]. We will often identify
$A/N(A) \cong \mathcal{O}(G_H)$
[Reference Waterhouse37, 11.7]. We will often identify
![]() $G_H$
with the space
$G_H$
with the space
![]() ${\textrm{Maxspec}}(A)$
of maximal ideals of A and with the group of algebra homomorphisms from A to k, that is with the group-like elements
${\textrm{Maxspec}}(A)$
of maximal ideals of A and with the group of algebra homomorphisms from A to k, that is with the group-like elements
![]() $G(A^{\circ})$
of the finite dual
$G(A^{\circ})$
of the finite dual
![]() $A^{\circ}$
. For
$A^{\circ}$
. For
![]() $g \in G_H$
, we denote the corresponding members of
$g \in G_H$
, we denote the corresponding members of
![]() ${\textrm{Maxspec}}(A)$
and
${\textrm{Maxspec}}(A)$
and
![]() $G(A^{\circ})$
by
$G(A^{\circ})$
by
![]() ${\mathfrak{m}}_g$
and
${\mathfrak{m}}_g$
and
![]() $\chi_g$
.
$\chi_g$
.
3. The finite dual
3.1 Commutative recap
When A is a commutative affine Hopf k-algebra the structure of
![]() $A^{\circ}$
is well understood—it is cocommutative and decomposes as a smash product
$A^{\circ}$
is well understood—it is cocommutative and decomposes as a smash product
by the classical structure theorem for cocommutative pointed Hopf algebras, due to Cartier–Gabriel–Kostant [Reference Montgomery26, Theorem 5.6.4(3)]. Here, A
′ is a connected Hopf subalgebra of A, and, as discussed in Section 2.2,
![]() $G = G(A^{\circ})$
is the group of characters of A. Moreover, when k has characteristic 0, A
′ is the enveloping algebra
$G = G(A^{\circ})$
is the group of characters of A. Moreover, when k has characteristic 0, A
′ is the enveloping algebra
![]() $U(\mathfrak{g})$
of the Lie algebra
$U(\mathfrak{g})$
of the Lie algebra
![]() $\mathfrak{g}$
of G, [Reference Montgomery26, Theorem 5.6.5]. That is,
$\mathfrak{g}$
of G, [Reference Montgomery26, Theorem 5.6.5]. That is,
![]() $\mathfrak{g}=(A^+/{A^+}^2)^{\ast}$
, consisting of the primitive elements of
$\mathfrak{g}=(A^+/{A^+}^2)^{\ast}$
, consisting of the primitive elements of
![]() $A^{\circ}$
, the functionals vanishing at 1 and
$A^{\circ}$
, the functionals vanishing at 1 and
![]() ${A^+}^2$
. Thus, by [Reference Montgomery26, Proposition 9.2.5],
${A^+}^2$
. Thus, by [Reference Montgomery26, Proposition 9.2.5],
where the first equality holds in general and the second when k has characteristic 0. Similarly, as can easily be checked, with no condition on the characteristic of k,
the functionals vanishing on some finite intersection of maximal ideals of A.
3.2 Subspaces and quotient spaces of
 $H^{\circ}$
$H^{\circ}$
The following lemma gathers together some basic facts concerning the components
![]() $A^{\circ}$
and
$A^{\circ}$
and
![]() $\overline{H}^{\ast}$
of
$\overline{H}^{\ast}$
of
![]() $H^{\circ}$
. Fix throughout the rest of the paper the Hopf embedding and the Hopf surjection
$H^{\circ}$
. Fix throughout the rest of the paper the Hopf embedding and the Hopf surjection
and the projection of right A-modules along X,
afforded by Theorem 2.2(8) when A is semiprime or central, or H is pointed.
Lemma 3.1. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf algebra and assume that A semiprime or central, or H is pointed.
$A \subseteq H$
be an affine commutative-by-finite Hopf algebra and assume that A semiprime or central, or H is pointed.
-
(1) There is an embedding of Hopf algebras
 \begin{equation*} \pi^{\circ} \;:\;\overline{H}^{\ast}\hookrightarrow H^{\circ}\;:\;\beta \mapsto \beta \circ \pi. \end{equation*}
\begin{equation*} \pi^{\circ} \;:\;\overline{H}^{\ast}\hookrightarrow H^{\circ}\;:\;\beta \mapsto \beta \circ \pi. \end{equation*}
-
(2)
 $\pi^\circ(\overline{H}^{\ast})$
, which we identify with
$\pi^\circ(\overline{H}^{\ast})$
, which we identify with
 $\overline{H}^{\ast}$
, is a normal Hopf subalgebra of
$\overline{H}^{\ast}$
, is a normal Hopf subalgebra of
 $H^{\circ}$
.
$H^{\circ}$
. -
(3)
 $H^{\circ}$
is a free (right and left)
$H^{\circ}$
is a free (right and left)
 $\overline{H}^{\ast}$
-module.
$\overline{H}^{\ast}$
-module. -
(4) There is a map of right
 $A^{\circ}$
-comodules
$A^{\circ}$
-comodules  \begin{equation*} \Pi^{\circ}\;:\;A^{\circ} \longrightarrow H^{\circ} \;:\;\alpha \mapsto \alpha \circ \Pi. \end{equation*}
\begin{equation*} \Pi^{\circ}\;:\;A^{\circ} \longrightarrow H^{\circ} \;:\;\alpha \mapsto \alpha \circ \Pi. \end{equation*}
-
(5) There is a Hopf algebra map
with \begin{equation*} \iota^{\circ} \;:\;H^{\circ} \longrightarrow A^{\circ} \;:\;f \mapsto f \circ \iota, \end{equation*}
\begin{equation*} \iota^{\circ} \;:\;H^{\circ} \longrightarrow A^{\circ} \;:\;f \mapsto f \circ \iota, \end{equation*}
 $\iota^{\circ} \circ \Pi^{\circ} = {\textrm{id}}_{A^{\circ}}.$
Thus
$\iota^{\circ} \circ \Pi^{\circ} = {\textrm{id}}_{A^{\circ}}.$
Thus
 $\Pi^{\circ}$
is injective and
$\Pi^{\circ}$
is injective and
 $\iota^{\circ}$
is surjective.
$\iota^{\circ}$
is surjective.
-
(6) Via
 $\iota^{\circ}$
,
$\iota^{\circ}$
,
 $H^{\circ}$
is canonically a right and left
$H^{\circ}$
is canonically a right and left
 $A^{\circ}$
-comodule algebra, with coinvariants
$A^{\circ}$
-comodule algebra, with coinvariants  \begin{equation*} (H^{\circ})^{co\,\iota^{\circ}}= {^{co\,\iota^{\circ}}(H^{\circ})}=\overline{H}^*. \end{equation*}
\begin{equation*} (H^{\circ})^{co\,\iota^{\circ}}= {^{co\,\iota^{\circ}}(H^{\circ})}=\overline{H}^*. \end{equation*}
-
(7) The Hopf ideal
 $(\overline{H}^{\ast})^+ H^{\circ}$
of
$(\overline{H}^{\ast})^+ H^{\circ}$
of
 $H^{\circ}$
is contained in
$H^{\circ}$
is contained in
 $\textrm{ker }\iota^{\circ}$
, so that (3.5)
$\textrm{ker }\iota^{\circ}$
, so that (3.5) \begin{equation} (\overline{H}^{\ast})^+ H^{\circ} \oplus \Pi^{\circ}(A^{\circ}) \subseteq \textrm{ker }\iota^{\circ} \oplus \Pi^{\circ}(A^{\circ}) = H^\circ.\end{equation}
\begin{equation} (\overline{H}^{\ast})^+ H^{\circ} \oplus \Pi^{\circ}(A^{\circ}) \subseteq \textrm{ker }\iota^{\circ} \oplus \Pi^{\circ}(A^{\circ}) = H^\circ.\end{equation}
Proof. (1),(2) Define
![]() $T \;:\!=\; \{f \in H^{\circ} \;:\;f(A^+H) = 0\}$
. Since
$T \;:\!=\; \{f \in H^{\circ} \;:\;f(A^+H) = 0\}$
. Since
![]() $A^+H$
is a Hopf ideal of H, it is clear that T is a Hopf subalgebra of
$A^+H$
is a Hopf ideal of H, it is clear that T is a Hopf subalgebra of
![]() $H^{\circ}$
which is isomorphic as a Hopf algebra to
$H^{\circ}$
which is isomorphic as a Hopf algebra to
![]() $\overline{H}^*$
, via the map
$\overline{H}^*$
, via the map
![]() $\pi^{\circ}\;:\;\overline{H}^{\ast} \longrightarrow H^{\circ}\;:\;\beta \mapsto \beta \circ \pi$
.
$\pi^{\circ}\;:\;\overline{H}^{\ast} \longrightarrow H^{\circ}\;:\;\beta \mapsto \beta \circ \pi$
.
Since
![]() $HA^+ = A^+ H$
by Theorem 2.2(2), it is very easy to check that
$HA^+ = A^+ H$
by Theorem 2.2(2), it is very easy to check that
To deduce normality of T, let
![]() $f\in\overline{H}^*$
and
$f\in\overline{H}^*$
and
![]() $\varphi\in H^{\circ}$
. For any
$\varphi\in H^{\circ}$
. For any
![]() $a\in A^+, h\in H$
,
$a\in A^+, h\in H$
,
 \begin{eqnarray*}(\textrm{ad}_{r} \varphi)(f) (ah) &=& \left[ \sum S^\circ(\varphi_1)f\varphi_2 \right](ah) = \sum S^\circ(\varphi_1)(a_1h_1) f(a_2h_2) \varphi_2(a_3h_3) \\&=& \sum \varphi_1(S(h_1)S(a_1)) \epsilon(a_2)f(h_2) \varphi_2(a_3h_3) = \sum \varphi(S(h_1)S(a_1)a_2h_3) f(h_2) \\&=& \epsilon(a) \sum \varphi(S(h_1)h_3) f(h_2) =0.\end{eqnarray*}
\begin{eqnarray*}(\textrm{ad}_{r} \varphi)(f) (ah) &=& \left[ \sum S^\circ(\varphi_1)f\varphi_2 \right](ah) = \sum S^\circ(\varphi_1)(a_1h_1) f(a_2h_2) \varphi_2(a_3h_3) \\&=& \sum \varphi_1(S(h_1)S(a_1)) \epsilon(a_2)f(h_2) \varphi_2(a_3h_3) = \sum \varphi(S(h_1)S(a_1)a_2h_3) f(h_2) \\&=& \epsilon(a) \sum \varphi(S(h_1)h_3) f(h_2) =0.\end{eqnarray*}
Similarly, one shows that
![]() $(\textrm{ad}_{\ell}\varphi)(ha) = 0$
for
$(\textrm{ad}_{\ell}\varphi)(ha) = 0$
for
![]() $h \in H$
and
$h \in H$
and
![]() $a \in A$
, and hence T is normal by (3.6).
$a \in A$
, and hence T is normal by (3.6).
(3) Since
![]() $\overline{H}^{\ast}$
is a finite-dimensional and normal Hopf subalgebra of
$\overline{H}^{\ast}$
is a finite-dimensional and normal Hopf subalgebra of
![]() $H^{\circ}$
,
$H^{\circ}$
,
![]() $H^{\circ}$
is a free
$H^{\circ}$
is a free
![]() $\overline{H}^{\ast}$
-module by [Reference Schneider31, Theorem 2.1(2)].
$\overline{H}^{\ast}$
-module by [Reference Schneider31, Theorem 2.1(2)].
(4),(5) Clearly, the restriction map
![]() $\iota^\circ\;:\;f \mapsto f \circ \iota$
is a Hopf algebra map whose image lies in
$\iota^\circ\;:\;f \mapsto f \circ \iota$
is a Hopf algebra map whose image lies in
![]() $A^{\circ}$
.
$A^{\circ}$
.
Let
![]() $f \in A^{\circ}$
, so
$f \in A^{\circ}$
, so
![]() $f(J) = 0$
for an ideal J of A of finite codimension. Thanks to Theorem 2.2(7)
$f(J) = 0$
for an ideal J of A of finite codimension. Thanks to Theorem 2.2(7)
![]() $H = A \oplus X$
for a right A-submodule X of H, so the left ideal HJ of H decomposes as a right A-module,
$H = A \oplus X$
for a right A-submodule X of H, so the left ideal HJ of H decomposes as a right A-module,
In view of (3.7), we can define
![]() $\widehat{f} \in H^{\ast}$
by
$\widehat{f} \in H^{\ast}$
by
![]() $\widehat{f}(X) = 0$
and
$\widehat{f}(X) = 0$
and
![]() $\widehat{f}_{\mid A} = f$
. Since
$\widehat{f}_{\mid A} = f$
. Since
![]() $\widehat{f}(HJ) = 0$
and
$\widehat{f}(HJ) = 0$
and
![]() $\textrm{dim}_k (H/HJ) < \infty$
,
$\textrm{dim}_k (H/HJ) < \infty$
,
![]() $\widehat{f} \in H^{\circ}$
by [Reference Montgomery26, Lemma 9.1.1]. By construction,
$\widehat{f} \in H^{\circ}$
by [Reference Montgomery26, Lemma 9.1.1]. By construction,
![]() $f \circ \Pi = \widehat{f}$
; that is,
$f \circ \Pi = \widehat{f}$
; that is,
![]() $\Pi^{\circ}(f) = \widehat{f}$
. It is clear that
$\Pi^{\circ}(f) = \widehat{f}$
. It is clear that
![]() $\iota^{\circ} \circ \Pi^{\circ} = \textrm{id}_{A^{\circ}}$
, so
$\iota^{\circ} \circ \Pi^{\circ} = \textrm{id}_{A^{\circ}}$
, so
![]() $\Pi^{\circ}$
is injective and
$\Pi^{\circ}$
is injective and
![]() $\iota^{\circ}$
surjective.
$\iota^{\circ}$
surjective.
It remains to prove that
![]() $\Pi^{\circ}$
is a map of right
$\Pi^{\circ}$
is a map of right
![]() $A^{\circ}$
-comodules. The right
$A^{\circ}$
-comodules. The right
![]() $A^{\circ}$
-comodule structure of
$A^{\circ}$
-comodule structure of
![]() $H^{\circ}$
is given by
$H^{\circ}$
is given by
![]() $\rho\;:\!=\;({\textrm{id}}\otimes \iota^{\circ})\Delta$
. Let
$\rho\;:\!=\;({\textrm{id}}\otimes \iota^{\circ})\Delta$
. Let
![]() $f\in A^{\circ}$
. Then for all
$f\in A^{\circ}$
. Then for all
![]() $a\in A, h\in H$
we have
$a\in A, h\in H$
we have
 \begin{eqnarray*}\left( (\rho\circ\Pi^\circ)(f)\right)(h\otimes a) &=& \left(\rho(f\circ\Pi)\right)(h\otimes a) = \left[ \sum (f\circ\Pi)_1 \otimes (f\circ\Pi)_2\circ\iota \right](h\otimes a) \\&=& \sum (f\circ\Pi)_1(h) (f\circ\Pi)_2 (a) = (f\circ\Pi)(ha) = f(\Pi(h)a).\end{eqnarray*}
\begin{eqnarray*}\left( (\rho\circ\Pi^\circ)(f)\right)(h\otimes a) &=& \left(\rho(f\circ\Pi)\right)(h\otimes a) = \left[ \sum (f\circ\Pi)_1 \otimes (f\circ\Pi)_2\circ\iota \right](h\otimes a) \\&=& \sum (f\circ\Pi)_1(h) (f\circ\Pi)_2 (a) = (f\circ\Pi)(ha) = f(\Pi(h)a).\end{eqnarray*}
On the other hand,
so (4) is proved.
(6)
![]() $H^{\circ}$
is canonically a right and left
$H^{\circ}$
is canonically a right and left
![]() $A^{\circ}$
-comodule algebra, the right comodule map being
$A^{\circ}$
-comodule algebra, the right comodule map being
![]() $\rho\;:\!=\;({\textrm{id}}\otimes\iota^{\circ})\circ\Delta$
. The right coinvariants are the maps f such that
$\rho\;:\!=\;({\textrm{id}}\otimes\iota^{\circ})\circ\Delta$
. The right coinvariants are the maps f such that
so that
![]() $f(ha)=f(h)\epsilon(a)$
for all
$f(ha)=f(h)\epsilon(a)$
for all
![]() $h\in H, a\in A$
. By (3.6), these are precisely the maps in
$h\in H, a\in A$
. By (3.6), these are precisely the maps in
![]() $\overline{H}^*$
. The left case is analogous.
$\overline{H}^*$
. The left case is analogous.
(7) First,
![]() $(\overline{H}^{\ast})^+ H^{\circ}$
is a Hopf ideal of
$(\overline{H}^{\ast})^+ H^{\circ}$
is a Hopf ideal of
![]() $H^{\circ}$
since, by (2),
$H^{\circ}$
since, by (2),
![]() $\overline{H}^{\ast}$
is a normal Hopf subalgebra of
$\overline{H}^{\ast}$
is a normal Hopf subalgebra of
![]() $H^{\circ}$
, so [Reference Montgomery26, Section 3.4] applies. Let
$H^{\circ}$
, so [Reference Montgomery26, Section 3.4] applies. Let
![]() $f\in (\overline{H}^*)^+$
. Then
$f\in (\overline{H}^*)^+$
. Then
![]() $f(A^+H)=0$
by definition of
$f(A^+H)=0$
by definition of
![]() $\overline{H}^{\ast}$
, and
$\overline{H}^{\ast}$
, and
![]() $\epsilon_{H^{\circ}}(f)=f(1)=0$
. Thus
$\epsilon_{H^{\circ}}(f)=f(1)=0$
. Thus
![]() $f(A)=0$
, so that
$f(A)=0$
, so that
![]() $f \in \textrm{ker }\iota^{\circ}$
. Hence
$f \in \textrm{ker }\iota^{\circ}$
. Hence
![]() $(\overline{H}^{\ast})^+ H^{\circ} \subseteq \textrm{ker }\iota^{\circ}$
, and the inclusion in (3.5) follows. For the equality in (3.5), first observe that the sums are direct by part (5). Let
$(\overline{H}^{\ast})^+ H^{\circ} \subseteq \textrm{ker }\iota^{\circ}$
, and the inclusion in (3.5) follows. For the equality in (3.5), first observe that the sums are direct by part (5). Let
![]() $f \in H^{\circ}$
. Then
$f \in H^{\circ}$
. Then
![]() $(\Pi^{\circ} \circ \iota^{\circ})(f) \in \Pi^{\circ}(A^{\circ})$
, and
$(\Pi^{\circ} \circ \iota^{\circ})(f) \in \Pi^{\circ}(A^{\circ})$
, and
so that
![]() $H^{\circ} = \textrm{ker }\iota^{\circ} + \Pi^{\circ}(A^{\circ})$
, as required.
$H^{\circ} = \textrm{ker }\iota^{\circ} + \Pi^{\circ}(A^{\circ})$
, as required.
3.3 Decomposition of
 $H^{\circ}$
$H^{\circ}$
Our first main result is the following. For the definition of a cleaving map, see Remark 2.3(2). Recall that Theorem 2.2(8) guarantees that under the hypotheses of the theorem below
![]() $H = A \oplus X$
for a right A-submodule X of H, and, as discussed in Section 1.1,
$H = A \oplus X$
for a right A-submodule X of H, and, as discussed in Section 1.1,
![]() $A \subseteq H$
satisfies
$A \subseteq H$
satisfies
![]() $(\mathbf{{CoSplit}})$
if X can be chosen to be a coideal of H.
$(\mathbf{{CoSplit}})$
if X can be chosen to be a coideal of H.
Theorem 3.2. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf k-algebra with A semiprime or central, or H pointed.
$A \subseteq H$
be an affine commutative-by-finite Hopf k-algebra with A semiprime or central, or H pointed.
-
(1) Suppose that H satisfies
 $(\mathbf{{CoSplit}})$
. Then
$(\mathbf{{CoSplit}})$
. Then
 $H^{\circ}$
decomposes as a smash product (3.8)the isomorphism (3.8) being as left
$H^{\circ}$
decomposes as a smash product (3.8)the isomorphism (3.8) being as left \begin{equation}H^{\circ}\; \cong \; \overline{H}^{\ast} \# A^{\circ},\end{equation}
\begin{equation}H^{\circ}\; \cong \; \overline{H}^{\ast} \# A^{\circ},\end{equation}
 $\overline{H}^*$
-modules and right
$\overline{H}^*$
-modules and right
 $A^{\circ}$
-comodules as well as of algebras.
$A^{\circ}$
-comodules as well as of algebras.
-
(2) Suppose that as an algebra
 $H=A\#_\sigma \overline{H}$
is a crossed product whose cleaving map
$H=A\#_\sigma \overline{H}$
is a crossed product whose cleaving map
 $\gamma\;:\;\overline{H}\to H$
is a coalgebra map. (For example, this is the case if H decomposes as a smash product
$\gamma\;:\;\overline{H}\to H$
is a coalgebra map. (For example, this is the case if H decomposes as a smash product
 $H \cong A \# \overline{H}$
with
$H \cong A \# \overline{H}$
with
 $\overline{H}$
a Hopf subalgebra of H.) Then (1) applies and the action of
$\overline{H}$
a Hopf subalgebra of H.) Then (1) applies and the action of
 $A^\circ$
on
$A^\circ$
on
 $\overline{H}^*$
is trivial, so that (3.9)as left
$\overline{H}^*$
is trivial, so that (3.9)as left \begin{equation} H^\circ \; \cong \; \overline{H}^{\ast}\otimes A^\circ\end{equation}
\begin{equation} H^\circ \; \cong \; \overline{H}^{\ast}\otimes A^\circ\end{equation}
 $\overline{H}^*$
-modules, right
$\overline{H}^*$
-modules, right
 $A^\circ$
-comodules and algebras.
$A^\circ$
-comodules and algebras.
Proof.
-
(1) Since
 $X=\textrm{ker }\Pi$
is a coideal of H,
$X=\textrm{ker }\Pi$
is a coideal of H,
 $\Pi$
is a coalgebra map, and so the right
$\Pi$
is a coalgebra map, and so the right
 $A^{\circ}$
-comodule map
$A^{\circ}$
-comodule map
 $\Pi^{\circ}$
of Lemma 3.1(4) is an algebra map. In particular, it is a cleaving map with convolution inverse
$\Pi^{\circ}$
of Lemma 3.1(4) is an algebra map. In particular, it is a cleaving map with convolution inverse
 $\Pi^{\circ}\circ S_{A^{\circ}}$
. By Remark 2.3(3),
$\Pi^{\circ}\circ S_{A^{\circ}}$
. By Remark 2.3(3),
 $ H^{\circ}$
is isomorphic to
$ H^{\circ}$
is isomorphic to
 $\overline{H}^* \#_\sigma A^{\circ} $
for some action of
$\overline{H}^* \#_\sigma A^{\circ} $
for some action of
 $A^{\circ}$
on
$A^{\circ}$
on
 $\overline{H}^*$
and cocycle
$\overline{H}^*$
and cocycle
 $\sigma$
. Since the cleaving map
$\sigma$
. Since the cleaving map
 $\Pi^{\circ}$
is an algebra map, the cocycle
$\Pi^{\circ}$
is an algebra map, the cocycle
 $\sigma$
is trivial. By [Reference Montgomery26, Proposition 7.2.3], the isomorphism carries the structures as stated.
$\sigma$
is trivial. By [Reference Montgomery26, Proposition 7.2.3], the isomorphism carries the structures as stated. -
(2) Since
 $\gamma$
is a coalgebra map,
$\gamma$
is a coalgebra map,
 $H=A\oplus A\gamma(\overline{H}^+)$
and
$H=A\oplus A\gamma(\overline{H}^+)$
and
 $A\gamma(\overline{H}^+)$
is a coideal of H, so (1) applies. It remains to prove the action is trivial, that is
$A\gamma(\overline{H}^+)$
is a coideal of H, so (1) applies. It remains to prove the action is trivial, that is
 $ \Pi^\circ(f')\pi^\circ(f) = \pi^\circ(f)\Pi^\circ(f'),$
for all
$ \Pi^\circ(f')\pi^\circ(f) = \pi^\circ(f)\Pi^\circ(f'),$
for all
 $f\in\overline{H}^*, f'\in A^\circ$
.
$f\in\overline{H}^*, f'\in A^\circ$
.
Let
![]() $f\in\overline{H}^*, f'\in A^\circ, a\in A, \bar{h}\in \overline{H}$
. We have
$f\in\overline{H}^*, f'\in A^\circ, a\in A, \bar{h}\in \overline{H}$
. We have
 \begin{eqnarray*}\pi^\circ(f)\Pi^\circ(f')(a\gamma(\bar{h})) &=& \sum \pi^\circ(f)(a_1\gamma(\bar{h_1}))\Pi^\circ(f')(a_2\gamma(\bar{h_2}))\\&=& \sum f\pi(a_1\gamma(\bar{h_1}))f'\Pi(a_2\gamma(\bar{h_2})) \\&=& \sum \epsilon(a_1)f\pi\gamma(\bar{h_1})f'(a_2)\epsilon(\gamma(\bar{h_2}))\\&=& \sum \epsilon(a_1)f(\bar{h_1})f'(a_2)\epsilon(\bar{h_2}) \\&=& f(\bar{h})f'(a),\end{eqnarray*}
\begin{eqnarray*}\pi^\circ(f)\Pi^\circ(f')(a\gamma(\bar{h})) &=& \sum \pi^\circ(f)(a_1\gamma(\bar{h_1}))\Pi^\circ(f')(a_2\gamma(\bar{h_2}))\\&=& \sum f\pi(a_1\gamma(\bar{h_1}))f'\Pi(a_2\gamma(\bar{h_2})) \\&=& \sum \epsilon(a_1)f\pi\gamma(\bar{h_1})f'(a_2)\epsilon(\gamma(\bar{h_2}))\\&=& \sum \epsilon(a_1)f(\bar{h_1})f'(a_2)\epsilon(\bar{h_2}) \\&=& f(\bar{h})f'(a),\end{eqnarray*}
since
![]() $\pi\circ\gamma = {\textrm{id}}$
, which follows from
$\pi\circ\gamma = {\textrm{id}}$
, which follows from
![]() $\gamma$
being a right
$\gamma$
being a right
![]() $\overline{H}$
-comodule coalgebra map. The proof for
$\overline{H}$
-comodule coalgebra map. The proof for
![]() $\Pi^\circ(f')\pi^\circ(f)$
is completely analogous.
$\Pi^\circ(f')\pi^\circ(f)$
is completely analogous.
Remark 3.3.
-
(1) In general the decompositions (3.8) and (3.9) are not isomorphisms of coalgebras. For instance, consider the group algebra
 $H=kD$
of the infinite dihedral group
$H=kD$
of the infinite dihedral group
 $D \;:\!=\; \langle a,b\;:\;a^2=1, aba=b^{-1} \rangle$
, with k of characteristic 0. It decomposes into
$D \;:\!=\; \langle a,b\;:\;a^2=1, aba=b^{-1} \rangle$
, with k of characteristic 0. It decomposes into
 $A\oplus X$
with
$A\oplus X$
with
 $A = k\langle b \rangle$
and
$A = k\langle b \rangle$
and
 $X = A(a-1)$
, so X is a coideal A-module and (3.8) applies. Here, where the algebra homomorphism indexed by
$X = A(a-1)$
, so X is a coideal A-module and (3.8) applies. Here, where the algebra homomorphism indexed by \begin{equation*} A^\circ \cong k[f]\otimes k(k^\times,\cdot),\end{equation*}
\begin{equation*} A^\circ \cong k[f]\otimes k(k^\times,\cdot),\end{equation*}
 $\lambda\in k^\times$
is
$\lambda\in k^\times$
is
 $\chi_\lambda$
, with
$\chi_\lambda$
, with
 $\chi_{\lambda}(b) = \lambda$
. Embedding
$\chi_{\lambda}(b) = \lambda$
. Embedding
 $A^{\circ}$
into
$A^{\circ}$
into
 $H^{\circ}$
using the algebra homomorphism
$H^{\circ}$
using the algebra homomorphism
 $\Pi^{\circ}$
, (3.8) yields the algebra structure However, the functional
$\Pi^{\circ}$
, (3.8) yields the algebra structure However, the functional \begin{equation*} H^{\circ} \; = \; kC_2 \otimes k[\Pi^{\circ}(f)] \otimes k\{\Pi^{\circ}(\chi_{\lambda}) \;:\;\lambda \in k^{\times}\}.\end{equation*}
\begin{equation*} H^{\circ} \; = \; kC_2 \otimes k[\Pi^{\circ}(f)] \otimes k\{\Pi^{\circ}(\chi_{\lambda}) \;:\;\lambda \in k^{\times}\}.\end{equation*}
 $\Pi^{\circ}(f)$
is not primitive and the functionals
$\Pi^{\circ}(f)$
is not primitive and the functionals
 $\Pi^{\circ}(\chi_\lambda)$
are not group-like (although they are units in
$\Pi^{\circ}(\chi_\lambda)$
are not group-like (although they are units in
 $H^{\circ}$
). Namely, one calculates:and
$H^{\circ}$
). Namely, one calculates:and \begin{equation*} \Delta(\Pi^{\circ}(f))=\Pi^{\circ}(f)\otimes 1 + \alpha\otimes \Pi^{\circ}(f); \end{equation*}
where the group-like involution
\begin{equation*} \Delta(\Pi^{\circ}(f))=\Pi^{\circ}(f)\otimes 1 + \alpha\otimes \Pi^{\circ}(f); \end{equation*}
where the group-like involution \begin{equation*} \Delta(\Pi^{\circ}(\chi_\lambda)) = \frac{1}{2} (\Pi^{\circ}(\chi_\lambda) \otimes \Pi^{\circ}(\chi_\lambda)) \left( (1+\alpha)\otimes 1 + (1-\alpha)\otimes\Pi^{\circ}(\chi_{\lambda^{-2}}) \right) , \end{equation*}
\begin{equation*} \Delta(\Pi^{\circ}(\chi_\lambda)) = \frac{1}{2} (\Pi^{\circ}(\chi_\lambda) \otimes \Pi^{\circ}(\chi_\lambda)) \left( (1+\alpha)\otimes 1 + (1-\alpha)\otimes\Pi^{\circ}(\chi_{\lambda^{-2}}) \right) , \end{equation*}
 $\alpha$
is the generator of
$\alpha$
is the generator of
 $\overline{H}^*=kC_2$
. For details, see [Reference Jahn19, Corollary 6.7, Remark 6.8] or [Reference Couto11, Corollary 4.4.6(II) and Appendix A.2]; there is also an extensive analysis of
$\overline{H}^*=kC_2$
. For details, see [Reference Jahn19, Corollary 6.7, Remark 6.8] or [Reference Couto11, Corollary 4.4.6(II) and Appendix A.2]; there is also an extensive analysis of
 $kD^{\circ}$
, arriving at the same formulae, in [Reference Ge and Liu16].
$kD^{\circ}$
, arriving at the same formulae, in [Reference Ge and Liu16].
-
(2) Note that the action of the smash product in (3.8) is given by
for any \begin{equation*} f\cdot\varphi = \sum \Pi^\circ(f_1)\varphi \Pi^\circ(S_{A^\circ} f_2), \end{equation*}
\begin{equation*} f\cdot\varphi = \sum \Pi^\circ(f_1)\varphi \Pi^\circ(S_{A^\circ} f_2), \end{equation*}
 $f\in A^\circ, \varphi\in\overline{H}^*$
. In particular, when k has characteristic 0, using the notation (3.1) and (3.2),
$f\in A^\circ, \varphi\in\overline{H}^*$
. In particular, when k has characteristic 0, using the notation (3.1) and (3.2),
 $\Pi^\circ(\mathfrak{g})\cong\mathfrak{g}$
and, if
$\Pi^\circ(\mathfrak{g})\cong\mathfrak{g}$
and, if
 $f\in\mathfrak{g}$
, then it acts as a derivation on
$f\in\mathfrak{g}$
, then it acts as a derivation on
 $\overline{H}^*$
(that is,
$\overline{H}^*$
(that is,
 $f\cdot \varphi = \Pi^\circ(f)\varphi - \varphi\Pi^\circ(f)$
), even though in general
$f\cdot \varphi = \Pi^\circ(f)\varphi - \varphi\Pi^\circ(f)$
), even though in general
 $\Pi^\circ(f)$
won’t be a primitive element of
$\Pi^\circ(f)$
won’t be a primitive element of
 $H^\circ$
. Similarly, if
$H^\circ$
. Similarly, if
 $\chi_g\in A^\circ$
denotes the algebra homomorphism corresponding to
$\chi_g\in A^\circ$
denotes the algebra homomorphism corresponding to
 $g\in G_H$
, then
$g\in G_H$
, then
 $\chi_g$
acts by conjugation over
$\chi_g$
acts by conjugation over
 $\overline{H}^*$
(i.e.
$\overline{H}^*$
(i.e.
 $\chi_g\cdot \varphi = \Pi^\circ(\chi_g)\varphi\Pi^\circ(\chi_{g^{-1}})$
), despite in general
$\chi_g\cdot \varphi = \Pi^\circ(\chi_g)\varphi\Pi^\circ(\chi_{g^{-1}})$
), despite in general
 $\Pi^\circ(\chi_g)$
not being a grouplike in
$\Pi^\circ(\chi_g)$
not being a grouplike in
 $H^\circ$
.
$H^\circ$
.
-
(3) The following question seems on the face of it to be rather optimistic, but we currently do not know any example of an affine commutative-by-finite Hopf algebra H for which there is no choice of the subalgebra A such that the answer is positive for
 $A \subseteq H$
.
$A \subseteq H$
.
Question 3.4. When
![]() $A \subseteq H$
is affine commutative-by-finite with A semiprime or central, or H pointed, is
$A \subseteq H$
is affine commutative-by-finite with A semiprime or central, or H pointed, is
![]() $H^{\circ}$
always a smash product of
$H^{\circ}$
always a smash product of
![]() $\overline{H}^{\ast}$
by
$\overline{H}^{\ast}$
by
![]() $A^{\circ}$
for a suitable choice of A?
$A^{\circ}$
for a suitable choice of A?
In Section 7, it is shown that Question 3.4 has a positive answer for many classes of commutative-by-finite Hopf algebras.
4. The tangential component
 $W(H^{\circ})$
$W(H^{\circ})$
4.1 Definition and basic properties
Throughout this section, the hypotheses and notation of Section 2.2 remain in force. We define an analogue for the finite dual of a commutative-by-finite Hopf algebra of the irreducible component A ′ appearing in (3.1), as follows.
Definition 4.1. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf k-algebra. The tangential component of
$A \subseteq H$
be an affine commutative-by-finite Hopf k-algebra. The tangential component of
![]() $H^{\circ}$
is
$H^{\circ}$
is
Lemma 4.2. Retain the notation and hypotheses of Definition 4.1.
-
(1)
 $W(H^{\circ})$
is a normal Hopf subalgebra of
$W(H^{\circ})$
is a normal Hopf subalgebra of
 $H^{\circ}$
.
$H^{\circ}$
. -
(2)
 $\overline{H}^*$
is a normal Hopf subalgebra of
$\overline{H}^*$
is a normal Hopf subalgebra of
 $W(H^{\circ})$
.
$W(H^{\circ})$
.
Proof. First,
![]() $W(H^{\circ})$
is a Hopf subalgebra because
$W(H^{\circ})$
is a Hopf subalgebra because
![]() $A^+H$
is a Hopf ideal of H and, for any Hopf ideal I of H,
$A^+H$
is a Hopf ideal of H and, for any Hopf ideal I of H,
is a Hopf subalgebra of
![]() $H^\circ$
by [Reference Montgomery26, Lemma 9.2.1]. Clearly,
$H^\circ$
by [Reference Montgomery26, Lemma 9.2.1]. Clearly,
![]() $W(H^{\circ})$
contains
$W(H^{\circ})$
contains
![]() $\overline{H}^*$
, by the definition of the latter subalgebra in Lemma 3.1(1). Since
$\overline{H}^*$
, by the definition of the latter subalgebra in Lemma 3.1(1). Since
![]() $\overline{H}^{\ast}$
is normal in
$\overline{H}^{\ast}$
is normal in
![]() $H^{\circ}$
by Lemma 3.1(2), it is a fortiori normal in the Hopf subalgebra
$H^{\circ}$
by Lemma 3.1(2), it is a fortiori normal in the Hopf subalgebra
![]() $W(H^{\circ})$
.
$W(H^{\circ})$
.
To prove normality of
![]() $W(H^\circ)$
let
$W(H^\circ)$
let
![]() $\varphi\in H^{\circ}$
and
$\varphi\in H^{\circ}$
and
![]() $f\in W(H^{\circ})$
, so f vanishes at
$f\in W(H^{\circ})$
, so f vanishes at
![]() $(A^+H)^n = (A^+)^n H$
for some positive integer n. Take
$(A^+H)^n = (A^+)^n H$
for some positive integer n. Take
![]() $a_1,\ldots, a_n\in A^+$
and
$a_1,\ldots, a_n\in A^+$
and
![]() $h\in H$
. Then
$h\in H$
. Then
 \begin{eqnarray*}&& \left[\sum S^\circ(\varphi_1)f\varphi_2\right](a_1\ldots a_nh) \\&=& \sum S^\circ(\varphi_1)(a_{1,1}\ldots a_{n,1}h_1)f(a_{1,2}\ldots a_{n,2}h_2)\varphi_2(a_{1,3}\ldots a_{n,3}h_3) \\&=&\sum \varphi_1(S(h_1)S(a_{n,1})\ldots S(a_{1,1}))f(a_{1,2}\ldots a_{n,2}h_2)\varphi_2(a_{1,3}\ldots a_{n,3}h_3) \\&=& \sum \varphi(S(h_1)S(a_{n,1})\ldots S(a_{1,1})a_{1,3}\ldots a_{n,3}h_3)f(a_{1,2}\ldots a_{n,2}h_2) \\&=& \sum \varphi(S(h_1)S(a_{n,1})a_{n,3}\ldots S(a_{1,1})a_{1,3} h_3)f(a_{1,2}\ldots a_{n,2}h_2),\end{eqnarray*}
\begin{eqnarray*}&& \left[\sum S^\circ(\varphi_1)f\varphi_2\right](a_1\ldots a_nh) \\&=& \sum S^\circ(\varphi_1)(a_{1,1}\ldots a_{n,1}h_1)f(a_{1,2}\ldots a_{n,2}h_2)\varphi_2(a_{1,3}\ldots a_{n,3}h_3) \\&=&\sum \varphi_1(S(h_1)S(a_{n,1})\ldots S(a_{1,1}))f(a_{1,2}\ldots a_{n,2}h_2)\varphi_2(a_{1,3}\ldots a_{n,3}h_3) \\&=& \sum \varphi(S(h_1)S(a_{n,1})\ldots S(a_{1,1})a_{1,3}\ldots a_{n,3}h_3)f(a_{1,2}\ldots a_{n,2}h_2) \\&=& \sum \varphi(S(h_1)S(a_{n,1})a_{n,3}\ldots S(a_{1,1})a_{1,3} h_3)f(a_{1,2}\ldots a_{n,2}h_2),\end{eqnarray*}
since A is commutative. For each i, we write
![]() $a_{i,2}=\epsilon(a_{i,2})1+a'_{\!\!i,2}$
, where
$a_{i,2}=\epsilon(a_{i,2})1+a'_{\!\!i,2}$
, where
![]() $a'_{\!\!i,2}\in A^+$
. Writing [1, n] for
$a'_{\!\!i,2}\in A^+$
. Writing [1, n] for
![]() $\lbrace 1,2,\ldots,n \rbrace$
, we now have
$\lbrace 1,2,\ldots,n \rbrace$
, we now have
 \begin{equation*} f(a_{1,2}\ldots a_{n,2}h_2)=\sum_{\mathcal{P}\subseteq [1,n]} \prod_{i\in\mathcal{P}}\epsilon(a_{i,2}) f\left(\prod_{i\in[1,n]\setminus\mathcal{P}}a'_{\!\!i,2}h_2\right). \end{equation*}
\begin{equation*} f(a_{1,2}\ldots a_{n,2}h_2)=\sum_{\mathcal{P}\subseteq [1,n]} \prod_{i\in\mathcal{P}}\epsilon(a_{i,2}) f\left(\prod_{i\in[1,n]\setminus\mathcal{P}}a'_{\!\!i,2}h_2\right). \end{equation*}
Therefore,
 \begin{eqnarray*}&&\left[\sum S^\circ(\varphi_1)f\varphi_2\right](a_1\ldots a_n h) \\&=& \sum \sum_{\mathcal{P}\subseteq[1,n]} \varphi(S(h_1)S(a_{n,1})a_{n,3}\ldots S(a_{1,1})a_{1,3} h_3) \prod_{i\in\mathcal{P}} \epsilon(a_{i,2}) f\left(\prod_{i\in[1,n]\setminus\mathcal{P}} a'_{\!\!i,2} \, h_2\right) \\&=& \sum \sum_{\mathcal{P}\subseteq[1,n]} \varphi \left(S(h_1) \prod_{i\in\mathcal{P}} S(a_{i,1})\epsilon(a_{i,2})a_{i,3} \prod_{i\in[1,n]\setminus\mathcal{P}} S(a_{i,1})a_{i,3} \, h_3 \right) f\left(\prod_{i\in[1,n]\setminus\mathcal{P}} a'_{\!\!i,2} h_2\right) \\&=& \sum \sum_{\mathcal{P}\subseteq[1,n]} \prod_{i\in\mathcal{P}} \epsilon(a_i) \, \varphi \left(S(h_1) \prod_{i\in[1,n]\setminus\mathcal{P}} S(a_{i,1})a_{i,3} \, h_3 \right) f\left(\prod_{i\in[1,n]\setminus\mathcal{P}} a'_{\!\!i,2} h_2\right).\end{eqnarray*}
\begin{eqnarray*}&&\left[\sum S^\circ(\varphi_1)f\varphi_2\right](a_1\ldots a_n h) \\&=& \sum \sum_{\mathcal{P}\subseteq[1,n]} \varphi(S(h_1)S(a_{n,1})a_{n,3}\ldots S(a_{1,1})a_{1,3} h_3) \prod_{i\in\mathcal{P}} \epsilon(a_{i,2}) f\left(\prod_{i\in[1,n]\setminus\mathcal{P}} a'_{\!\!i,2} \, h_2\right) \\&=& \sum \sum_{\mathcal{P}\subseteq[1,n]} \varphi \left(S(h_1) \prod_{i\in\mathcal{P}} S(a_{i,1})\epsilon(a_{i,2})a_{i,3} \prod_{i\in[1,n]\setminus\mathcal{P}} S(a_{i,1})a_{i,3} \, h_3 \right) f\left(\prod_{i\in[1,n]\setminus\mathcal{P}} a'_{\!\!i,2} h_2\right) \\&=& \sum \sum_{\mathcal{P}\subseteq[1,n]} \prod_{i\in\mathcal{P}} \epsilon(a_i) \, \varphi \left(S(h_1) \prod_{i\in[1,n]\setminus\mathcal{P}} S(a_{i,1})a_{i,3} \, h_3 \right) f\left(\prod_{i\in[1,n]\setminus\mathcal{P}} a'_{\!\!i,2} h_2\right).\end{eqnarray*}
The summands where
![]() $\mathcal{P}\neq\emptyset$
vanish due to
$\mathcal{P}\neq\emptyset$
vanish due to
![]() $\epsilon(a_i)=0$
for all
$\epsilon(a_i)=0$
for all
![]() $i\in[1,n]$
and the summands where
$i\in[1,n]$
and the summands where
![]() $\mathcal{P}=\emptyset$
vanish because f is zero on
$\mathcal{P}=\emptyset$
vanish because f is zero on
![]() $(A^+H)^n={A^+}^nH$
. The proof for the left adjoint action is similar, so normality of
$(A^+H)^n={A^+}^nH$
. The proof for the left adjoint action is similar, so normality of
![]() $W(H^{\circ})$
in
$W(H^{\circ})$
in
![]() $H^{\circ}$
is proved.
$H^{\circ}$
is proved.
4.2 Decomposition of
 $W(H^\circ)$
$W(H^\circ)$
To analyse the structure of
![]() $W(H^{\circ}) $
, we use the Hopf algebra surjection
$W(H^{\circ}) $
, we use the Hopf algebra surjection
![]() $\iota^{\circ}$
from
$\iota^{\circ}$
from
![]() $H^{\circ}$
to
$H^{\circ}$
to
![]() $A^{\circ}$
of Lemma 3.1(5), given by restriction of functionals from H to A. In the following result, we decompose
$A^{\circ}$
of Lemma 3.1(5), given by restriction of functionals from H to A. In the following result, we decompose
![]() $W(H^\circ)$
into the crossed product
$W(H^\circ)$
into the crossed product
![]() $\overline{H}^* \#_\sigma A'$
. Notice that the isomorphism (4.1) below does not require hypothesis (CoSplit), in contrast to Theorem 3.2.
$\overline{H}^* \#_\sigma A'$
. Notice that the isomorphism (4.1) below does not require hypothesis (CoSplit), in contrast to Theorem 3.2.
Theorem 4.3. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf algebra with A semiprime or central, or H pointed. Recall that
$A \subseteq H$
be an affine commutative-by-finite Hopf algebra with A semiprime or central, or H pointed. Recall that
![]() $A^{\circ}$
decomposes as
$A^{\circ}$
decomposes as
![]() $A' \#kG_H$
as in (3.1).
$A' \#kG_H$
as in (3.1).
-
(1)
 $\iota^{\circ}(W(H^{\circ})) = A'$
.
$\iota^{\circ}(W(H^{\circ})) = A'$
. -
(2)
 $W(H^{\circ})$
decomposes as a crossed product for a cocycle
$W(H^{\circ})$
decomposes as a crossed product for a cocycle
 $\sigma$
and an action of A
′ on
$\sigma$
and an action of A
′ on
 $\overline{H}^*$
. That is, as algebras, left
$\overline{H}^*$
. That is, as algebras, left
 $\overline{H}^{\ast}$
-modules and right A
′-comodules, (4.1)
$\overline{H}^{\ast}$
-modules and right A
′-comodules, (4.1) \begin{equation} W(H^{\circ})\cong \overline{H}^* \#_\sigma A'.\end{equation}
\begin{equation} W(H^{\circ})\cong \overline{H}^* \#_\sigma A'.\end{equation}
-
(3)
 $W(H^{\circ})^{\textrm{co } \iota^\circ_{\mid_{W(H^\circ)}}} = \overline{H}^{\ast}.$
$W(H^{\circ})^{\textrm{co } \iota^\circ_{\mid_{W(H^\circ)}}} = \overline{H}^{\ast}.$
-
(4) Suppose that k has characteristic 0. Then
 $\textrm{ker } \iota^\circ_{\mid_{W(H^\circ)}} = (\overline{H}^{\ast})^+ W(H^{\circ}).$
$\textrm{ker } \iota^\circ_{\mid_{W(H^\circ)}} = (\overline{H}^{\ast})^+ W(H^{\circ}).$
-
(5) Suppose that
 $A \subseteq H$
satisfies (CoSplit). Then
$A \subseteq H$
satisfies (CoSplit). Then
 $\sigma$
is trivial—that is, (4.1) is a decomposition of
$\sigma$
is trivial—that is, (4.1) is a decomposition of
 $W(H^{\circ})$
as a smash product. When k has characteristic 0, so that
$W(H^{\circ})$
as a smash product. When k has characteristic 0, so that
 $A' = U(\mathfrak{g})$
, the action of
$A' = U(\mathfrak{g})$
, the action of
 $U(\mathfrak{g})$
on
$U(\mathfrak{g})$
on
 $\overline{H}^*$
is given by for
$\overline{H}^*$
is given by for \begin{equation*} f \cdot \varphi = \Pi^\circ(f) \varphi - \varphi\Pi^\circ(f), \end{equation*}
\begin{equation*} f \cdot \varphi = \Pi^\circ(f) \varphi - \varphi\Pi^\circ(f), \end{equation*}
 $f\in\mathfrak{g}, \varphi\in\overline{H}^*$
. That is,
$f\in\mathfrak{g}, \varphi\in\overline{H}^*$
. That is,
 $W(H^\circ)$
is a differential operator ring over
$W(H^\circ)$
is a differential operator ring over
 $\overline{H}^*$
.
$\overline{H}^*$
.
Proof. (1) Since
![]() $\iota^{\circ}$
is just restriction of functionals to the subdomain A, it is clear that
$\iota^{\circ}$
is just restriction of functionals to the subdomain A, it is clear that
![]() $\iota^{\circ}(W(H^{\circ})) \subseteq A'$
. To see that
$\iota^{\circ}(W(H^{\circ})) \subseteq A'$
. To see that
![]() $\textrm{im } \iota^{\circ}_{\mid_{W(H^\circ)}} = A'$
, note the definition (3.2) of A
′, and then observe that, in the proof of Lemma 3.1(4), if
$\textrm{im } \iota^{\circ}_{\mid_{W(H^\circ)}} = A'$
, note the definition (3.2) of A
′, and then observe that, in the proof of Lemma 3.1(4), if
![]() $f \in A' \subseteq A^{\circ}$
, then the map
$f \in A' \subseteq A^{\circ}$
, then the map
![]() $\widehat{f} \in H^{\circ}$
constructed there, with
$\widehat{f} \in H^{\circ}$
constructed there, with
![]() $\Pi^{\circ}(f) = \widehat{f}$
, is actually in
$\Pi^{\circ}(f) = \widehat{f}$
, is actually in
![]() $W(H^{\circ})$
. Since
$W(H^{\circ})$
. Since
![]() $\iota^{\circ} \circ \Pi^{\circ} = {\textrm{id}}_{A^{\circ}}$
by Lemma 3.1(5),
$\iota^{\circ} \circ \Pi^{\circ} = {\textrm{id}}_{A^{\circ}}$
by Lemma 3.1(5),
![]() $\iota^{\circ}(\widehat{f}) = f$
and the result follows.
$\iota^{\circ}(\widehat{f}) = f$
and the result follows.
(2),(3): By Lemma 3.1(6),
![]() $H^{\circ}$
is a right
$H^{\circ}$
is a right
![]() $A^{\circ}$
-comodule algebra with
$A^{\circ}$
-comodule algebra with
![]() $\rho=({\textrm{id}}\otimes\iota^{\circ})\Delta$
. In particular, since
$\rho=({\textrm{id}}\otimes\iota^{\circ})\Delta$
. In particular, since
![]() $W(H^{\circ})$
is a Hopf subalgebra of
$W(H^{\circ})$
is a Hopf subalgebra of
![]() $H^{\circ}$
by Lemma 4.2(2), and using (1) of the present theorem,
$H^{\circ}$
by Lemma 4.2(2), and using (1) of the present theorem,
That is, the structure of right
![]() $A^{\circ}$
-comodule of
$A^{\circ}$
-comodule of
![]() $H^{\circ}$
restricts to a structure of right A
′-comodule on
$H^{\circ}$
restricts to a structure of right A
′-comodule on
![]() $W(H^{\circ})$
.
$W(H^{\circ})$
.
We have noted in the proof of (1) that the right
![]() $A^{\circ}$
-comodule map
$A^{\circ}$
-comodule map
![]() $\Pi^{\circ}\;:\;A^{\circ} \longrightarrow H^{\circ}$
maps A
′ into
$\Pi^{\circ}\;:\;A^{\circ} \longrightarrow H^{\circ}$
maps A
′ into
![]() $W(H^{\circ})$
. Thus, in light of (4.2),
$W(H^{\circ})$
. Thus, in light of (4.2),
![]() $\Pi^{\circ}_{\mid_{A'}}\;:\;A' \longrightarrow W(H^{\circ})$
is an injection of right A
′-comodules.
$\Pi^{\circ}_{\mid_{A'}}\;:\;A' \longrightarrow W(H^{\circ})$
is an injection of right A
′-comodules.
A linear map from a coalgebra to an algebra is convolution invertible if and only if its restriction to the coradical is convolution invertible, see [Reference Takeuchi35, Lemma 14] or [Reference Montgomery26, Lemma 5.2.10]. But A
′ is connected by its definition as the irreducible component of the coalgebra
![]() $A^{\circ}$
containing
$A^{\circ}$
containing
![]() $\varepsilon$
, [Reference Montgomery26, p. 78]; that is, its coradical is k. Therefore, in the language of Remark 2.3(3),
$\varepsilon$
, [Reference Montgomery26, p. 78]; that is, its coradical is k. Therefore, in the language of Remark 2.3(3),
![]() $\Pi^{\circ}_{\mid_{A'}}$
is a cleaving map and by the result of Doi and Takeuchi recalled in Remark 2.3(3),
$\Pi^{\circ}_{\mid_{A'}}$
is a cleaving map and by the result of Doi and Takeuchi recalled in Remark 2.3(3),
Since the A
′-comodule structure of
![]() $W(H^{\circ})$
is the restriction of the
$W(H^{\circ})$
is the restriction of the
![]() $A^{\circ}$
-comodule structure of
$A^{\circ}$
-comodule structure of
![]() $H^{\circ}$
, it follows from Lemma 3.1(6) that
$H^{\circ}$
, it follows from Lemma 3.1(6) that
(4) Since
![]() $\textrm{char}k = 0$
,
$\textrm{char}k = 0$
,
![]() $A' = U(\mathfrak{g})$
by (3.2). It is clear from (4.1) that
$A' = U(\mathfrak{g})$
by (3.2). It is clear from (4.1) that
Moreover, we know from Lemma 3.1(7) that
By (1),
![]() $\textrm{im } \iota^\circ_{\mid_{W(H^\circ)}} = U(\mathfrak{g})$
. Since A is affine,
$\textrm{im } \iota^\circ_{\mid_{W(H^\circ)}} = U(\mathfrak{g})$
. Since A is affine,
![]() $\mathfrak{g}$
is finite dimensional, and hence
$\mathfrak{g}$
is finite dimensional, and hence
![]() $U(\mathfrak{g})$
is a noetherian algebra. In particular,
$U(\mathfrak{g})$
is a noetherian algebra. In particular,
![]() $U(\mathfrak{g})$
cannot be isomorphic to a proper factor of itself, and hence (4.3) must be an equality, proving (4).
$U(\mathfrak{g})$
cannot be isomorphic to a proper factor of itself, and hence (4.3) must be an equality, proving (4).
(5) This follows from (2) and Theorem 3.2(1), since the cocycle
![]() $\sigma$
in (2) is in this case trivial by the latter result. The last part is a special case of Remark 3.3(2).
$\sigma$
in (2) is in this case trivial by the latter result. The last part is a special case of Remark 3.3(2).
Recall that, in characteristic 0, a finite dimensional Hopf algebra is semisimple if and only if cosemisimple [Reference Larson and Radford21], so the following improvement of Theorem 4.3(5) applies when
![]() $\overline{H}$
is semisimple if k has characteristic 0.
$\overline{H}$
is semisimple if k has characteristic 0.
Corollary 4.4. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf k-algebra with A semiprime or central, or H pointed. Retain the additional notation of Theorem 4.3. Assume that
$A \subseteq H$
be an affine commutative-by-finite Hopf k-algebra with A semiprime or central, or H pointed. Retain the additional notation of Theorem 4.3. Assume that
![]() $A \subseteq H$
satisfies hypothesis (CoSplit), and that
$A \subseteq H$
satisfies hypothesis (CoSplit), and that
![]() $\overline{H}$
is cosemisimple. Then the action of
$\overline{H}$
is cosemisimple. Then the action of
![]() $U(\mathfrak{g})$
on
$U(\mathfrak{g})$
on
![]() $\overline{H}^{\ast}$
is inner, so that, as algebras,
$\overline{H}^{\ast}$
is inner, so that, as algebras,
Proof. By Theorem 4.3(5)
![]() $W(H^{\ast})$
is a smash product of algebras,
$W(H^{\ast})$
is a smash product of algebras,
By our hypothesis,
![]() $\overline{H}^{\ast}$
is semisimple, and so by Jacobson’s theorem, (see for example [Reference Montgomery26, Example 6.1.6, Proposition 6.2.1 and discussion following]), since k is algebraically closed,
$\overline{H}^{\ast}$
is semisimple, and so by Jacobson’s theorem, (see for example [Reference Montgomery26, Example 6.1.6, Proposition 6.2.1 and discussion following]), since k is algebraically closed,
![]() $\mathfrak{g}$
acts by inner derivations on
$\mathfrak{g}$
acts by inner derivations on
![]() $\overline{H}^{\ast}$
. That is, there is a copy
$\overline{H}^{\ast}$
. That is, there is a copy
![]() $u(\mathfrak{g})$
of
$u(\mathfrak{g})$
of
![]() $\mathfrak{g}$
contained in
$\mathfrak{g}$
contained in
![]() $\overline{H}^{\ast}$
, (where we view
$\overline{H}^{\ast}$
, (where we view
![]() $\overline{H}^{\ast}$
as a Lie algebra via the commutator bracket), such that for all
$\overline{H}^{\ast}$
as a Lie algebra via the commutator bracket), such that for all
![]() $x \in \mathfrak{g}$
and
$x \in \mathfrak{g}$
and
![]() $h \in \overline{H}^{\ast}$
,
$h \in \overline{H}^{\ast}$
,
Replacing the copy of
![]() $\mathfrak{g}$
appearing in (4.4) with the isomorphic Lie algebra
$\mathfrak{g}$
appearing in (4.4) with the isomorphic Lie algebra
where
![]() $\{x_i \}$
is a k-basis of
$\{x_i \}$
is a k-basis of
![]() $\mathfrak{g}$
, we see that
$\mathfrak{g}$
, we see that
as claimed.
5. The subcoalgebra
 $\widehat{kG_H}$
$\widehat{kG_H}$
5.1 Orbits in
 ${\textrm{Maxspec}}(A)$
${\textrm{Maxspec}}(A)$
Recall the description (3.3) in Section 3.1 of the Hopf subalgebra kG of
![]() $A^{\circ}$
. In this section, we extend this viewpoint to H, defining a subcoalgebra
$A^{\circ}$
. In this section, we extend this viewpoint to H, defining a subcoalgebra
![]() $\widehat{kG_H}$
of
$\widehat{kG_H}$
of
![]() $H^{\circ}$
which is a Hopf subalgebra under mild additional hypotheses and which reduces to
$H^{\circ}$
which is a Hopf subalgebra under mild additional hypotheses and which reduces to
![]() $kG_H$
when
$kG_H$
when
![]() $H = A$
. We saw in Theorem 2.2(3) that the left adjoint action of H on A factors over the ideal
$H = A$
. We saw in Theorem 2.2(3) that the left adjoint action of H on A factors over the ideal
![]() $A^+ H$
, so that A is a left
$A^+ H$
, so that A is a left
![]() $\overline{H}$
-module algebra. An ideal I of A is said to be
$\overline{H}$
-module algebra. An ideal I of A is said to be
![]() $\overline{H}$
-stable if
$\overline{H}$
-stable if
Since the extension
![]() $A\subseteq H$
is faithfully flat by Theorem 2.2(4), I is
$A\subseteq H$
is faithfully flat by Theorem 2.2(4), I is
![]() $\overline{H}$
-stable if and only if
$\overline{H}$
-stable if and only if
![]() $HI=IH$
.
$HI=IH$
.
Definition 5.1. Let T be a Hopf algebra and R a left T-module algebra, with V a subspace of R. The T-core of V is the subspace
Note that if V is a right or left ideal of R in Definition 5.1 then so is
![]() $V^{(T)}$
. The crucial parts (2) and (3) of the following result are essentially due to Skryabin [Reference Skryabin33, Theorems 1.1, 1.3]. For the proofs of Proposition 5.2 and Corollary 5.4, see [Reference Brown and Couto3, Proposition 4.4].
$V^{(T)}$
. The crucial parts (2) and (3) of the following result are essentially due to Skryabin [Reference Skryabin33, Theorems 1.1, 1.3]. For the proofs of Proposition 5.2 and Corollary 5.4, see [Reference Brown and Couto3, Proposition 4.4].
Proposition 5.2. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf algebra and let
$A \subseteq H$
be an affine commutative-by-finite Hopf algebra and let
![]() ${\mathfrak{m}}\in{\textrm{Maxspec}}(A)$
.
${\mathfrak{m}}\in{\textrm{Maxspec}}(A)$
.
-
(1)
 ${\mathfrak{m}}^{(\overline{H})}$
is the largest
${\mathfrak{m}}^{(\overline{H})}$
is the largest
 $\overline{H}$
-stable ideal of A contained in
$\overline{H}$
-stable ideal of A contained in
 ${\mathfrak{m}}$
.
${\mathfrak{m}}$
. -
(2)
 $A/{\mathfrak{m}}^{(\overline{H})}$
is an
$A/{\mathfrak{m}}^{(\overline{H})}$
is an
 $\overline{H}$
-simple algebra - that is, the
$\overline{H}$
-simple algebra - that is, the
 $\overline{H}$
-core of each of its proper ideals is
$\overline{H}$
-core of each of its proper ideals is
 $\{0\}$
.
$\{0\}$
. -
(3)
 $A/{\mathfrak{m}}^{(\overline{H})}$
is a Frobenius algebra. In particular,
$A/{\mathfrak{m}}^{(\overline{H})}$
is a Frobenius algebra. In particular,
 $A/{\mathfrak{m}}^{(\overline{H})}$
is finite dimensional.
$A/{\mathfrak{m}}^{(\overline{H})}$
is finite dimensional.
Following still Skryabin, we can use Proposition 5.2(2) to extend the fundamental idea that a group of automorphisms of the algebra A defines orbits in
![]() ${\textrm{Maxspec}} (A)$
, to the present setting where the group is replaced by a Hopf algebra.
${\textrm{Maxspec}} (A)$
, to the present setting where the group is replaced by a Hopf algebra.
Definition 5.3. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf algebra.
$A \subseteq H$
be an affine commutative-by-finite Hopf algebra.
-
(1) For each
 ${\mathfrak{m}}\in{\textrm{Maxspec}}(A)$
, its
${\mathfrak{m}}\in{\textrm{Maxspec}}(A)$
, its
 $\overline{H}$
-orbit is the set of maximal ideals with the same
$\overline{H}$
-orbit is the set of maximal ideals with the same
 $\overline{H}$
-core,
$\overline{H}$
-core,  \begin{equation*}\mathcal{O}_{{\mathfrak{m}}} = \lbrace {\mathfrak{m}}'\in{\textrm{Maxspec}}(A)\;:\;{{\mathfrak{m}}'}^{(\overline{H})} = {\mathfrak{m}}^{(\overline{H})} \rbrace. \end{equation*}
\begin{equation*}\mathcal{O}_{{\mathfrak{m}}} = \lbrace {\mathfrak{m}}'\in{\textrm{Maxspec}}(A)\;:\;{{\mathfrak{m}}'}^{(\overline{H})} = {\mathfrak{m}}^{(\overline{H})} \rbrace. \end{equation*}
-
(2) Define an equivalence relation
 $\sim^{(\overline{H})}$
on
$\sim^{(\overline{H})}$
on
 $G_H = {\textrm{Maxspec}}(A)$
as follows: for
$G_H = {\textrm{Maxspec}}(A)$
as follows: for
 $g,h\in G_H$
,
$g,h\in G_H$
,
 $g\sim^{(\overline{H})} h$
if and only if
$g\sim^{(\overline{H})} h$
if and only if
 $ {\mathfrak{m}}_g^{(\overline{H})}={\mathfrak{m}}_h^{(\overline{H})}.$
$ {\mathfrak{m}}_g^{(\overline{H})}={\mathfrak{m}}_h^{(\overline{H})}.$
It’s clear that
![]() $\sim^{(\overline{H})}$
is an equivalence relation; but it is far from obvious, although it follows easily from Proposition 5.2(2), that the
$\sim^{(\overline{H})}$
is an equivalence relation; but it is far from obvious, although it follows easily from Proposition 5.2(2), that the
![]() $\overline{H}$
-orbits have the following simple description.
$\overline{H}$
-orbits have the following simple description.
Corollary 5.4. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf algebra.
$A \subseteq H$
be an affine commutative-by-finite Hopf algebra.
-
(1)
 $\mathcal{O}_{{\mathfrak{m}}} = \lbrace {\mathfrak{m}}'\in{\textrm{Maxspec}}(A)\;:\;{\mathfrak{m}}^{(\overline{H})}\subseteq {\mathfrak{m}}' \rbrace$
.
$\mathcal{O}_{{\mathfrak{m}}} = \lbrace {\mathfrak{m}}'\in{\textrm{Maxspec}}(A)\;:\;{\mathfrak{m}}^{(\overline{H})}\subseteq {\mathfrak{m}}' \rbrace$
. -
(2)
 $\mathcal{O}_{{\mathfrak{m}}}$
is finite.
$\mathcal{O}_{{\mathfrak{m}}}$
is finite.
5.2 Orbital semisimplicity
The results in Section 5.1 lead naturally to:
Definition 5.5. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf algebra. Then
$A \subseteq H$
be an affine commutative-by-finite Hopf algebra. Then
![]() $A \subseteq H$
is called orbitally semisimple if
$A \subseteq H$
is called orbitally semisimple if
![]() $A/{\mathfrak{m}}^{(\overline{H})}$
is semisimple for all
$A/{\mathfrak{m}}^{(\overline{H})}$
is semisimple for all
![]() ${\mathfrak{m}}\in{\textrm{Maxspec}}(A)$
. In this case we write that
${\mathfrak{m}}\in{\textrm{Maxspec}}(A)$
. In this case we write that
![]() $A \subseteq H$
satisfies
$A \subseteq H$
satisfies
![]() $(\mathbf{{OrbSemi}})$
.
$(\mathbf{{OrbSemi}})$
.
Note that, in view of Corollary 5.4(1),
![]() $A \subseteq H$
is orbitally semisimple if and only if
$A \subseteq H$
is orbitally semisimple if and only if
Since we have used the left adjoint action in Definition 5.5, one might choose to call the above property left orbital semisimplicity; but in fact it is shown in [Reference Brown and Couto3, Lemma 4.10(2)] that
![]() $A \subseteq H$
is left orbitally semisimple if and only if it is right orbitally semisimple.
$A \subseteq H$
is left orbitally semisimple if and only if it is right orbitally semisimple.
We know no examples of affine commutative-by-finite Hopf algebras that are not orbitally semisimple. When A is central in H orbital semsimplicity is trivial; the next result lists other positive cases. In characteristic 0, there are overlaps between these, thanks to the result of Etingof and Walton [Reference Etingof and Walton15] implying that the action of
![]() $\overline{H}$
factors through a group algebra when
$\overline{H}$
factors through a group algebra when
![]() $\overline{H}$
is semisimple and cosemisimple and A is a domain.
$\overline{H}$
is semisimple and cosemisimple and A is a domain.
Theorem 5.6 ([Reference Brown and Couto3, Theorem 4.8]). The affine commutative-by-finite Hopf algebra
![]() $A\subseteq H$
satisfies
$A\subseteq H$
satisfies
![]() $(\mathbf{{OrbSemi}})$
in the following cases.
$(\mathbf{{OrbSemi}})$
in the following cases.
-
(1) The adjoint action of
 $\overline{H}$
on
$\overline{H}$
on
 ${\textrm{Maxspec}}(A)$
factors through a group.
${\textrm{Maxspec}}(A)$
factors through a group. -
(2)
 $\overline{H}$
is cosemisimple.
$\overline{H}$
is cosemisimple. -
(3)
 $\overline{H}$
is involutory and either
$\overline{H}$
is involutory and either
 $\textrm{char } k=0$
or
$\textrm{char } k=0$
or
 $\textrm{char } k>\textrm{dim}_k (A/{\mathfrak{m}}^{(\overline{H})})$
for all
$\textrm{char } k>\textrm{dim}_k (A/{\mathfrak{m}}^{(\overline{H})})$
for all
 ${\mathfrak{m}}\in{\textrm{Maxspec}}(A)$
.
${\mathfrak{m}}\in{\textrm{Maxspec}}(A)$
.
We discuss particular families of examples of affine commutative-by-finite Hopf algebras, and their status with respect to orbital semisimplicity, in Section 7.
5.3 The character component of
 $H^{\circ}$
$H^{\circ}$
Here is the definition, we have been working towards:
Definition 5.7. Let H be an affine commutative-by-finite Hopf algebra, finite over the normal commutative Hopf subalgebra A. Recall from Section 2.2 that
![]() $G_H$
denotes the affine algebraic k-group such that
$G_H$
denotes the affine algebraic k-group such that
![]() $A/N(A) \cong \mathcal{O}(G_H)$
.
$A/N(A) \cong \mathcal{O}(G_H)$
.
-
(1) The character component of
 $H^\circ$
is
$H^\circ$
is  \begin{equation*} \widehat{kG_H} = \left\{ f\in H^{\circ}\;:\;\,f\left( H {\mathfrak{m}}_{g_1}^{(\overline{H})} \cap \ldots \cap H {\mathfrak{m}}_{g_r}^{(\overline{H})} \right)=0, \text{ for some } g_1,\ldots,g_r\in G_H/\sim^{(\overline{H})} \right\}. \end{equation*}
\begin{equation*} \widehat{kG_H} = \left\{ f\in H^{\circ}\;:\;\,f\left( H {\mathfrak{m}}_{g_1}^{(\overline{H})} \cap \ldots \cap H {\mathfrak{m}}_{g_r}^{(\overline{H})} \right)=0, \text{ for some } g_1,\ldots,g_r\in G_H/\sim^{(\overline{H})} \right\}. \end{equation*}
-
(2) For
 $g \in G_H$
, write
$g \in G_H$
, write
 $\widehat{g}$
to denote the subspace
$\widehat{g}$
to denote the subspace
 $(H/H {\mathfrak{m}}_g^{(\overline{H})})^{\ast}$
of
$(H/H {\mathfrak{m}}_g^{(\overline{H})})^{\ast}$
of
 $\widehat{kG_H}$
.
$\widehat{kG_H}$
.
Here are some basic properties of these spaces.
Lemma 5.8. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf k-algebra. Retain the notation of Section 2.2 and Definition 5.7.
$A \subseteq H$
be an affine commutative-by-finite Hopf k-algebra. Retain the notation of Section 2.2 and Definition 5.7.
-
(1) If
 $g,h \in G_H$
with
$g,h \in G_H$
with
 $g \sim^{(\overline{H})} h$
, then
$g \sim^{(\overline{H})} h$
, then
 $\widehat{g} = \widehat{h}$
.
$\widehat{g} = \widehat{h}$
. -
(2)
 $\widehat{kG_H}=\bigoplus_{g\in G_H/\sim^{(\overline{H})}} \; \widehat{g}$
.
$\widehat{kG_H}=\bigoplus_{g\in G_H/\sim^{(\overline{H})}} \; \widehat{g}$
. -
(3)
 $\widehat{kG_H}$
is a subcoalgebra of
$\widehat{kG_H}$
is a subcoalgebra of
 $H^{\circ}$
.
$H^{\circ}$
. -
(4) For all
 $g \in G_H$
,
$g \in G_H$
,
 $\widehat{g}$
is a subcoalgebra of
$\widehat{g}$
is a subcoalgebra of
 $\widehat{kG_H}$
.
$\widehat{kG_H}$
. -
(5) For all
 $g \in G_H$
, and
$g \in G_H$
, and \begin{equation*} \widehat{g} \supseteq \bigoplus_{h \sim^{(\overline{H})} g} \left( H/H {\mathfrak{m}}_h \right)^{\ast} ,\end{equation*}
\begin{equation*} \widehat{g} \supseteq \bigoplus_{h \sim^{(\overline{H})} g} \left( H/H {\mathfrak{m}}_h \right)^{\ast} ,\end{equation*}
 \begin{equation*} \left( H/H {\mathfrak{m}}_g \right)^{\ast} \supseteq \overline{H}^{\ast} \Pi^{\circ}(\chi_g) + \Pi^\circ(\chi_g)\overline{H}^{\ast}. \end{equation*}
\begin{equation*} \left( H/H {\mathfrak{m}}_g \right)^{\ast} \supseteq \overline{H}^{\ast} \Pi^{\circ}(\chi_g) + \Pi^\circ(\chi_g)\overline{H}^{\ast}. \end{equation*}
-
(6) For
 $g \in G_H$
,
$g \in G_H$
,
 $S^{\circ}(\widehat{g})\; =\; \widehat{g^{-1}}$
.
$S^{\circ}(\widehat{g})\; =\; \widehat{g^{-1}}$
. -
(7)
 $\widehat{kG_H}\cap W(H^{\circ})\; =\; \overline{H}^{\ast} \; =\; \widehat{1_G}$
.
$\widehat{kG_H}\cap W(H^{\circ})\; =\; \overline{H}^{\ast} \; =\; \widehat{1_G}$
. -
(8) Assume that A is a domain and let
 $d_A(H)$
be the minimal number of generators of H as a right or left A-module. For
$d_A(H)$
be the minimal number of generators of H as a right or left A-module. For
 $g \in G_H$
, (5.2)and
$g \in G_H$
, (5.2)and \begin{equation} \textrm{dim}_k (H/H{\mathfrak{m}}_g) = \textrm{dim}_k (H/{\mathfrak{m}}_g H) = \textrm{dim}_k (\overline{H}),\end{equation}
(5.3)If H is prime (which implies that A is a domain), then
\begin{equation} \textrm{dim}_k (H/H{\mathfrak{m}}_g) = \textrm{dim}_k (H/{\mathfrak{m}}_g H) = \textrm{dim}_k (\overline{H}),\end{equation}
(5.3)If H is prime (which implies that A is a domain), then \begin{equation} \textrm{dim}_k(\widehat{g}) \; = \; \textrm{dim}_k (A/{\mathfrak{m}}_g^{(\overline{H})}) \textrm{dim}_k(\overline{H}) \leq d_A(H)\textrm{dim}_k(\overline{H}).\end{equation}
(5.4)
\begin{equation} \textrm{dim}_k(\widehat{g}) \; = \; \textrm{dim}_k (A/{\mathfrak{m}}_g^{(\overline{H})}) \textrm{dim}_k(\overline{H}) \leq d_A(H)\textrm{dim}_k(\overline{H}).\end{equation}
(5.4) \begin{equation} \textrm{dim}_k(\widehat{g}) \; \leq \; \left(\textrm{dim}_k (\overline{H})\right)^2.\end{equation}
\begin{equation} \textrm{dim}_k(\widehat{g}) \; \leq \; \left(\textrm{dim}_k (\overline{H})\right)^2.\end{equation}
Proof. (1) This follows from the definition of
![]() $\sim^{(\overline{H})}$
.
$\sim^{(\overline{H})}$
.
(2) If
![]() $g, h \in G_H$
with
$g, h \in G_H$
with
![]() $\mathcal{O}_{{\mathfrak{m}}_g} \neq \mathcal{O}_{{\mathfrak{m}}_h}$
, then the ideals
$\mathcal{O}_{{\mathfrak{m}}_g} \neq \mathcal{O}_{{\mathfrak{m}}_h}$
, then the ideals
![]() ${\mathfrak{m}}_g^{(\overline{H})}$
and
${\mathfrak{m}}_g^{(\overline{H})}$
and
![]() ${\mathfrak{m}}_h^{(\overline{H})}$
of A are comaximal, by Corollary 5.4(1). The same is thus true of the ideals
${\mathfrak{m}}_h^{(\overline{H})}$
of A are comaximal, by Corollary 5.4(1). The same is thus true of the ideals
![]() $H{\mathfrak{m}}_g^{(\overline{H})}$
and
$H{\mathfrak{m}}_g^{(\overline{H})}$
and
![]() $H{\mathfrak{m}}_h^{(\overline{H})}$
of H. Therefore, if
$H{\mathfrak{m}}_h^{(\overline{H})}$
of H. Therefore, if
![]() $g_1, \ldots , g_r \in G_H$
are representatives of distinct
$g_1, \ldots , g_r \in G_H$
are representatives of distinct
![]() $\sim^{(\overline{H})}$
-orbits, the Chinese Remainder Theorem shows that
$\sim^{(\overline{H})}$
-orbits, the Chinese Remainder Theorem shows that
 \begin{equation*} \left. H \middle/ \bigcap_{i=1}^r H{\mathfrak{m}}_{g_i}^{(\overline{H})} \right. \cong \bigoplus_{i=1}^r H/H{\mathfrak{m}}_{g_i}^{(\overline{H})}. \end{equation*}
\begin{equation*} \left. H \middle/ \bigcap_{i=1}^r H{\mathfrak{m}}_{g_i}^{(\overline{H})} \right. \cong \bigoplus_{i=1}^r H/H{\mathfrak{m}}_{g_i}^{(\overline{H})}. \end{equation*}
Taking duals on both sides proves (2).
(3),(4): Let
![]() $g \in G_H$
. That
$g \in G_H$
. That
![]() $\widehat{g}$
is a subcoalgebra of
$\widehat{g}$
is a subcoalgebra of
![]() $H^{\circ}$
is simply a special case of the elementary fact that, for an ideal I of finite codimension in an algebra R,
$H^{\circ}$
is simply a special case of the elementary fact that, for an ideal I of finite codimension in an algebra R,
![]() $(R/I)^{\ast}$
is a subcoalgebra of
$(R/I)^{\ast}$
is a subcoalgebra of
![]() $R^{\circ}$
. So (3) and (4) follow from this observation together with (2).
$R^{\circ}$
. So (3) and (4) follow from this observation together with (2).
(5) The first inclusion is clear. For the second, note first that
by the definition of the coproduct in
![]() $A/N(A) = \mathcal{O}(G_H)$
, combined with the fact that N(A) is a Hopf ideal of A, [Reference Brown and Couto3, Lemma 5.2(1)]. Let
$A/N(A) = \mathcal{O}(G_H)$
, combined with the fact that N(A) is a Hopf ideal of A, [Reference Brown and Couto3, Lemma 5.2(1)]. Let
![]() $f \in \overline{H}^{\ast}$
. Then, using (5.5),
$f \in \overline{H}^{\ast}$
. Then, using (5.5),
So
![]() $\overline{H}^{\ast}\Pi^{\circ}(\chi_g) \subseteq (H/H{\mathfrak{m}}_g)^{\ast}$
. The proof of the remaining inclusion is similar.
$\overline{H}^{\ast}\Pi^{\circ}(\chi_g) \subseteq (H/H{\mathfrak{m}}_g)^{\ast}$
. The proof of the remaining inclusion is similar.
(6) Let
![]() $g \in G_H$
. To prove that
$g \in G_H$
. To prove that
![]() $S^{\circ}(\widehat{g})=\widehat{g^{-1}}$
it suffices to show that
$S^{\circ}(\widehat{g})=\widehat{g^{-1}}$
it suffices to show that
![]() $S({\mathfrak{m}}_g^{(\overline{H})}) = {\mathfrak{m}}_{g^{-1}}^{(\overline{H})}$
. It is easy to see that
$S({\mathfrak{m}}_g^{(\overline{H})}) = {\mathfrak{m}}_{g^{-1}}^{(\overline{H})}$
. It is easy to see that
Since S is an algebra anti-isomorphism of H with
![]() $S(A)=A$
, it follows that
$S(A)=A$
, it follows that
This proves (6).
(7) The final equality is clear from the definitions, and this also shows that
![]() $\overline{H}^{\ast} \subseteq \widehat{kG_H}$
. Thus, by Lemma 4.2(2),
$\overline{H}^{\ast} \subseteq \widehat{kG_H}$
. Thus, by Lemma 4.2(2),
![]() $\overline{H}^{\ast}\subseteq W(H^{\circ}) \cap \widehat{kG_H}$
.
$\overline{H}^{\ast}\subseteq W(H^{\circ}) \cap \widehat{kG_H}$
.
For the reverse inclusion, suppose
![]() $f \in H^{\circ}$
with f vanishing on
$f \in H^{\circ}$
with f vanishing on
![]() $(A^+H)^n={A^+}^nH$
and also on
$(A^+H)^n={A^+}^nH$
and also on
![]() $I \;:\!=\; \bigcap_{i=1}^r {\mathfrak{m}}_{g_i}^{(\overline{H})}H$
, for some
$I \;:\!=\; \bigcap_{i=1}^r {\mathfrak{m}}_{g_i}^{(\overline{H})}H$
, for some
![]() $n,r \geq 1$
and distinct
$n,r \geq 1$
and distinct
![]() $g_1,\ldots,g_r\in G_H/\sim^{(\overline{H})}$
. We claim that
$g_1,\ldots,g_r\in G_H/\sim^{(\overline{H})}$
. We claim that
If
![]() $g_i\neq 1_{G_H}$
for all
$g_i\neq 1_{G_H}$
for all
![]() $i = 1, \ldots , r$
, then I and
$i = 1, \ldots , r$
, then I and
![]() ${A^+}^nH$
are comaximal by the discussion in the proof of (2), so that (5.6) is clear. Suppose on the other hand that, say,
${A^+}^nH$
are comaximal by the discussion in the proof of (2), so that (5.6) is clear. Suppose on the other hand that, say,
![]() $g_1 = 1_{G_H}$
. Then
$g_1 = 1_{G_H}$
. Then
![]() $I + {A^+}^nH \subseteq A^+ H$
, and the left A-module
$I + {A^+}^nH \subseteq A^+ H$
, and the left A-module
![]() $A^+H/(I + {A^+}^n H)$
is annihilated by both of the comaximal ideals
$A^+H/(I + {A^+}^n H)$
is annihilated by both of the comaximal ideals
![]() ${A^+}^{n-1}$
and by
${A^+}^{n-1}$
and by
![]() $\bigcap_{i=2}^r{\mathfrak{m}}_{g_i}^{(\overline{H})}$
. Hence
$\bigcap_{i=2}^r{\mathfrak{m}}_{g_i}^{(\overline{H})}$
. Hence
![]() $A^+H/(I + {A^+}^n H) = \{0\}$
and again (5.6) is proved. Thus (5.6) holds in all cases and so
$A^+H/(I + {A^+}^n H) = \{0\}$
and again (5.6) is proved. Thus (5.6) holds in all cases and so
![]() $f \in \overline{H}^{\ast}$
, as required.
$f \in \overline{H}^{\ast}$
, as required.
(8) Assume that A is a domain. Localise A at the maximal ideal
![]() ${\mathfrak{m}}_g$
, and consider the left
${\mathfrak{m}}_g$
, and consider the left
![]() $A_{{\mathfrak{m}}_g}$
-module
$A_{{\mathfrak{m}}_g}$
-module
![]() $H_{{\mathfrak{m}}_g} \;:\!=\; A_{{\mathfrak{m}}_g} \otimes_A H$
. Since H is a finitely generated projective A-module by Theorem 2.2(6), and
$H_{{\mathfrak{m}}_g} \;:\!=\; A_{{\mathfrak{m}}_g} \otimes_A H$
. Since H is a finitely generated projective A-module by Theorem 2.2(6), and
![]() $A_{{\mathfrak{m}}_g}$
is local,
$A_{{\mathfrak{m}}_g}$
is local,
![]() $H_{{\mathfrak{m}}_g} $
is a free
$H_{{\mathfrak{m}}_g} $
is a free
![]() $A_{{\mathfrak{m}}_g}$
-module of finite rank r. Let Q denote the quotient field of A. Since H is a torsion free A-module,
$A_{{\mathfrak{m}}_g}$
-module of finite rank r. Let Q denote the quotient field of A. Since H is a torsion free A-module,
so r is constant as g varies through
![]() $G_H$
. Taking
$G_H$
. Taking
![]() $g = 1_{G_H}$
and applying Nakayama’s lemma,
$g = 1_{G_H}$
and applying Nakayama’s lemma,
proving the second equality in (5.2). The first equality is a consequence of the second, using the antipode. Since the algebra
![]() $H/{\mathfrak{m}}_{g}^{(\overline{H})}H$
is artinian, it is isomorphic as an
$H/{\mathfrak{m}}_{g}^{(\overline{H})}H$
is artinian, it is isomorphic as an
![]() $A/{\mathfrak{m}}_g^{(\overline{H})}$
-module to the factor
$A/{\mathfrak{m}}_g^{(\overline{H})}$
-module to the factor
![]() $H_{{\mathfrak{m}}_g}/{\mathfrak{m}}_{g}^{(\overline{H})}H_{{\mathfrak{m}}_g}$
of
$H_{{\mathfrak{m}}_g}/{\mathfrak{m}}_{g}^{(\overline{H})}H_{{\mathfrak{m}}_g}$
of
![]() $H_{{\mathfrak{m}}_g}$
. But the latter is a free
$H_{{\mathfrak{m}}_g}$
. But the latter is a free
![]() $A/{\mathfrak{m}}_{g}^{(\overline{H})}$
-module of rank r. Combining this with (5.7) proves the equality in (5.3), and the inequality is then given by [Reference Brown and Couto3, Theorem 6.1(2)]. If H is prime then A is a domain and the inequality (5.4) follows from [Reference Brown and Couto3, Corollary 6.2 and its proof].
$A/{\mathfrak{m}}_{g}^{(\overline{H})}$
-module of rank r. Combining this with (5.7) proves the equality in (5.3), and the inequality is then given by [Reference Brown and Couto3, Theorem 6.1(2)]. If H is prime then A is a domain and the inequality (5.4) follows from [Reference Brown and Couto3, Corollary 6.2 and its proof].
5.4 Subalgebras and subcoalgebras of
 $\widehat{kG_H}$
$\widehat{kG_H}$
In order to better control the structure of
![]() $\widehat{kG_H}$
, we need to impose on the inclusion
$\widehat{kG_H}$
, we need to impose on the inclusion
![]() $A \subseteq H$
one or both of the additional hypotheses
$A \subseteq H$
one or both of the additional hypotheses
![]() $(\mathbf{{CoSplit}})$
and
$(\mathbf{{CoSplit}})$
and
![]() $(\mathbf{{OrbSemi}})$
defined respectively in Section 1.1 and Definition 5.5. First we assume
$(\mathbf{{OrbSemi}})$
defined respectively in Section 1.1 and Definition 5.5. First we assume
![]() $(\mathbf{{CoSplit}})$
in Proposition 5.9, then
$(\mathbf{{CoSplit}})$
in Proposition 5.9, then
![]() $(\mathbf{{OrbSemi}})$
in Proposition 5.10, before combining these in Theorem 5.13.
$(\mathbf{{OrbSemi}})$
in Proposition 5.10, before combining these in Theorem 5.13.
Proposition 5.9. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf k-algebra satisfying
$A \subseteq H$
be an affine commutative-by-finite Hopf k-algebra satisfying
![]() $(\mathbf{{CoSplit}})$
. Assume also that A is semiprime or central, or that H is pointed. Keep the notation introduced in Sections 5.3 and 2.2 and in Lemma 3.1. Define
$(\mathbf{{CoSplit}})$
. Assume also that A is semiprime or central, or that H is pointed. Keep the notation introduced in Sections 5.3 and 2.2 and in Lemma 3.1. Define
-
(1)
 $\widetilde{G_H}$
is a subgroup of the group of units of
$\widetilde{G_H}$
is a subgroup of the group of units of
 $H^{\circ}$
, and the algebra injection
$H^{\circ}$
, and the algebra injection
 $\Pi^{\circ}\;:\;A^{\circ} \to H^{\circ}$
restricts to an isomorphism of groups from the group-likes
$\Pi^{\circ}\;:\;A^{\circ} \to H^{\circ}$
restricts to an isomorphism of groups from the group-likes
 $G_H$
of
$G_H$
of
 $A^{\circ}$
to
$A^{\circ}$
to
 $\widetilde{G_H}$
.
$\widetilde{G_H}$
. -
(2) The subalgebra of
 $H^{\circ}$
generated by
$H^{\circ}$
generated by
 $\widetilde{G_H}$
is the group algebra
$\widetilde{G_H}$
is the group algebra
 $k\widetilde{G_H}$
, and
$k\widetilde{G_H}$
, and
 $\Pi^{\circ}$
restricts to an algebra isomorphism from
$\Pi^{\circ}$
restricts to an algebra isomorphism from
 $kG_H$
to
$kG_H$
to
 $k\widetilde{G_H}$
.
$k\widetilde{G_H}$
. -
(3) For all
 $g \in G_H$
,
$g \in G_H$
,
 $\overline{H}^{\ast}\Pi^{\circ}(\chi_g) = \Pi^{\circ}(\chi_g)\overline{H}^{\ast}$
is free of rank 1 as an
$\overline{H}^{\ast}\Pi^{\circ}(\chi_g) = \Pi^{\circ}(\chi_g)\overline{H}^{\ast}$
is free of rank 1 as an
 $\overline{H}^{\ast}$
-bimodule. Hence
$\overline{H}^{\ast}$
-bimodule. Hence
 $\langle \overline{H}^{\ast}, \widetilde{G_H} \rangle$
is a skew group algebra
$\langle \overline{H}^{\ast}, \widetilde{G_H} \rangle$
is a skew group algebra
 $\overline{H}^{\ast} \# \widetilde{G_H}$
; that is, is a subalgebra of
$\overline{H}^{\ast} \# \widetilde{G_H}$
; that is, is a subalgebra of \begin{equation*} \langle \overline{H}^{\ast}, \widetilde{G_H} \rangle \; = \; \overline{H}^{\ast} \# \widetilde{G_H} \; = \; \oplus_{g \in G_H} \overline{H}^{\ast}\Pi^{\circ}(\chi_g) \end{equation*}
\begin{equation*} \langle \overline{H}^{\ast}, \widetilde{G_H} \rangle \; = \; \overline{H}^{\ast} \# \widetilde{G_H} \; = \; \oplus_{g \in G_H} \overline{H}^{\ast}\Pi^{\circ}(\chi_g) \end{equation*}
 $H^{\circ}$
contained in the subcoalgebra
$H^{\circ}$
contained in the subcoalgebra
 $\widehat{kG_H}$
.
$\widehat{kG_H}$
.
-
(4) There are inclusions
If A is a domain then the second inclusion is an equality. \begin{equation*} \widehat{kG_H} = \bigoplus_{g \in G_H/\sim^{(\overline{H})}} \widehat{g} \supseteq \bigoplus_{g \in G_H/\sim^{(\overline{H})}}\left(\bigoplus_{h\sim^{(\overline{H})} g} (H/H\mathfrak{m}_h)^{\ast}\right) \supseteq \bigoplus_{g \in G_H/\sim^{(\overline{H})}}\left(\bigoplus_{h\sim^{(\overline{H})} g} \overline{H}^{\ast}\Pi^{\circ}(\chi_h)\right) = \overline{H}^{\ast} \# \widetilde{G_H}. \end{equation*}
\begin{equation*} \widehat{kG_H} = \bigoplus_{g \in G_H/\sim^{(\overline{H})}} \widehat{g} \supseteq \bigoplus_{g \in G_H/\sim^{(\overline{H})}}\left(\bigoplus_{h\sim^{(\overline{H})} g} (H/H\mathfrak{m}_h)^{\ast}\right) \supseteq \bigoplus_{g \in G_H/\sim^{(\overline{H})}}\left(\bigoplus_{h\sim^{(\overline{H})} g} \overline{H}^{\ast}\Pi^{\circ}(\chi_h)\right) = \overline{H}^{\ast} \# \widetilde{G_H}. \end{equation*}
Proof. (1),(2) The
![]() $(\mathbf{{CoSplit}})$
hypothesis ensures that
$(\mathbf{{CoSplit}})$
hypothesis ensures that
![]() $\Pi$
is a coalgebra map, so
$\Pi$
is a coalgebra map, so
![]() $\Pi^\circ$
is an algebra homomorphism, and is an injection by Lemma 3.1(5). Thus
$\Pi^\circ$
is an algebra homomorphism, and is an injection by Lemma 3.1(5). Thus
![]() $\Pi^{\circ}$
maps
$\Pi^{\circ}$
maps
![]() $G_H$
isomorphically to a subgroup
$G_H$
isomorphically to a subgroup
![]() $\widetilde{G_H}$
of the group of units of
$\widetilde{G_H}$
of the group of units of
![]() $H^{\circ}$
, and
$H^{\circ}$
, and
(3) By Remark 3.3(2), the action of
![]() $kG_H\subset A^\circ$
on
$kG_H\subset A^\circ$
on
![]() $\overline{H}^*$
is
$\overline{H}^*$
is
for any
![]() $f\in \overline{H}^*, g\in G_H$
, hence
$f\in \overline{H}^*, g\in G_H$
, hence
![]() $\Pi^\circ(\chi_g)f\in \overline{H}^*\Pi^\circ(\chi_g)$
, proving
$\Pi^\circ(\chi_g)f\in \overline{H}^*\Pi^\circ(\chi_g)$
, proving
![]() $\Pi^\circ(\chi_g)\overline{H}^* \subseteq \overline{H}^*\Pi^\circ(\chi_g)$
and the converse is proved similarly. Both these
$\Pi^\circ(\chi_g)\overline{H}^* \subseteq \overline{H}^*\Pi^\circ(\chi_g)$
and the converse is proved similarly. Both these
![]() $\overline{H}^{\ast}$
-modules are free of rank 1 since
$\overline{H}^{\ast}$
-modules are free of rank 1 since
![]() $\Pi^{\circ}(G_H)$
consists of units of
$\Pi^{\circ}(G_H)$
consists of units of
![]() $H^{\circ}$
. From Theorem 3.2(1) and its proof, we know that
$H^{\circ}$
. From Theorem 3.2(1) and its proof, we know that
![]() $H^{\circ}$
is a free left and right
$H^{\circ}$
is a free left and right
![]() $\overline{H}^{\ast}$
-module with any vector space basis of
$\overline{H}^{\ast}$
-module with any vector space basis of
![]() $\Pi^{\circ}(A^{\circ})$
as free basis. In particular,
$\Pi^{\circ}(A^{\circ})$
as free basis. In particular,
![]() $\{\Pi^{\circ}(\chi_g) \;:\;g \in G_H \}$
spans a free left and right
$\{\Pi^{\circ}(\chi_g) \;:\;g \in G_H \}$
spans a free left and right
![]() $\overline{H}^{\circ}$
-submodule of
$\overline{H}^{\circ}$
-submodule of
![]() $\widehat{kG_H}$
.
$\widehat{kG_H}$
.
(4) The first equality and first inclusion are immediate from Definition 5.7 and Lemma 5.8(5). The second inclusion follows from Lemma 5.8(5) and the third equality is part (3) of the present lemma. If A is a domain the second inclusion is seen to be an equality by comparing vector space dimensions using Lemma 5.8(8).
We examine next the effect of the
![]() $(\mathbf{{OrbSemi}})$
hypothesis on
$(\mathbf{{OrbSemi}})$
hypothesis on
![]() $\widehat{kG_H}$
.
$\widehat{kG_H}$
.
Proposition 5.10. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf algebra satisfying
$A \subseteq H$
be an affine commutative-by-finite Hopf algebra satisfying
![]() $(\mathbf{{OrbSemi}})$
.
$(\mathbf{{OrbSemi}})$
.
-
(1) The subcoalgebra
 $\widehat{kG_H}$
of
$\widehat{kG_H}$
of
 $H^{\circ}$
is a Hopf subalgebra.
$H^{\circ}$
is a Hopf subalgebra. -
(2) For
 $g,h \in G_H$
, (5.8)
$g,h \in G_H$
, (5.8) \begin{equation}\widehat{g}\widehat{h}\subseteq \sum_{g'\sim^{({\overline{H}})} g, h'\sim^{({\overline{H}})} h} \widehat{g'h'}.\end{equation}
\begin{equation}\widehat{g}\widehat{h}\subseteq \sum_{g'\sim^{({\overline{H}})} g, h'\sim^{({\overline{H}})} h} \widehat{g'h'}.\end{equation}
-
(3) For
 $g \in G_H$
,
$g \in G_H$
,
 $\widehat{g}$
is a left and right
$\widehat{g}$
is a left and right
 $\overline{H}^{\ast}$
-module. Assume further that A is a domain. Then, for any
$\overline{H}^{\ast}$
-module. Assume further that A is a domain. Then, for any
 $g\in G_H$
:
$g\in G_H$
: -
(4)
 $\textrm{dim}_k (\widehat{g}) = \left|\mathcal{O}_{{\mathfrak{m}}_g}\right| \, \textrm{dim}_k (\overline{H}).$
$\textrm{dim}_k (\widehat{g}) = \left|\mathcal{O}_{{\mathfrak{m}}_g}\right| \, \textrm{dim}_k (\overline{H}).$
-
(5)
 \begin{equation*} \widehat{g} = \bigoplus_{h \sim^{({\overline{H}})} g} \left( H/H{\mathfrak{m}}_h \right)^{\ast} = \bigoplus_{h \sim^{({\overline{H}})} g}\left( H/ {\mathfrak{m}}_hH \right)^{\ast}. \end{equation*}
\begin{equation*} \widehat{g} = \bigoplus_{h \sim^{({\overline{H}})} g} \left( H/H{\mathfrak{m}}_h \right)^{\ast} = \bigoplus_{h \sim^{({\overline{H}})} g}\left( H/ {\mathfrak{m}}_hH \right)^{\ast}. \end{equation*}
Proof. Note that (3) is a special case of (2), since
![]() $\overline{H}^{\ast} = \widehat{1_{G_H}}$
. By Lemma 5.8(3),(6), (1) will follow if
$\overline{H}^{\ast} = \widehat{1_{G_H}}$
. By Lemma 5.8(3),(6), (1) will follow if
![]() $\widehat{kG_H}$
is closed under multiplication. Moreover, by Lemma 5.8(2), closure under multiplication will follow at once from (2). We claim that to prove (5.8) amounts to showing that
$\widehat{kG_H}$
is closed under multiplication. Moreover, by Lemma 5.8(2), closure under multiplication will follow at once from (2). We claim that to prove (5.8) amounts to showing that
 \begin{equation}\Delta\left( \bigcap_{g'\sim^{(\overline{H})} g, h'\sim^{(\overline{H})} h} {\mathfrak{m}}_{g'h'} \right)\subseteq {\mathfrak{m}}_g^{(\overline{H})}\otimes A + A\otimes {\mathfrak{m}}_h^{(\overline{H})} =\;:\;J.\end{equation}
\begin{equation}\Delta\left( \bigcap_{g'\sim^{(\overline{H})} g, h'\sim^{(\overline{H})} h} {\mathfrak{m}}_{g'h'} \right)\subseteq {\mathfrak{m}}_g^{(\overline{H})}\otimes A + A\otimes {\mathfrak{m}}_h^{(\overline{H})} =\;:\;J.\end{equation}
For, the flatness of H over A together with the Chinese remainder theorem implies that
![]() $\bigcap_{g',h'} (H{\mathfrak{m}}_{g'h'}^{(\overline{H})}) = H\left(\bigcap_{g',h'} {\mathfrak{m}}_{g'h'}^{(\overline{H})}\right)$
. Hence, given (5.9),
$\bigcap_{g',h'} (H{\mathfrak{m}}_{g'h'}^{(\overline{H})}) = H\left(\bigcap_{g',h'} {\mathfrak{m}}_{g'h'}^{(\overline{H})}\right)$
. Hence, given (5.9),
 \begin{equation} \Delta\left(\bigcap_{g'\sim^{({\overline{H}})} g, h'\sim^{({\overline{H}})} h} H{\mathfrak{m}}_{g'h'}^{(\overline{H})}\right) \subseteq H{\mathfrak{m}}_g^{(\overline{H})}\otimes H + H \otimes H{\mathfrak{m}}_h^{(\overline{H})}.\end{equation}
\begin{equation} \Delta\left(\bigcap_{g'\sim^{({\overline{H}})} g, h'\sim^{({\overline{H}})} h} H{\mathfrak{m}}_{g'h'}^{(\overline{H})}\right) \subseteq H{\mathfrak{m}}_g^{(\overline{H})}\otimes H + H \otimes H{\mathfrak{m}}_h^{(\overline{H})}.\end{equation}
Consider now
![]() $\beta\gamma $
for
$\beta\gamma $
for
![]() $\beta \in\widehat{g}$
and
$\beta \in\widehat{g}$
and
![]() $\gamma \in\widehat{h}$
. It follows from (5.10) that
$\gamma \in\widehat{h}$
. It follows from (5.10) that
 \begin{equation*} \beta \gamma \left( \bigcap_{g'\sim^{({\overline{H}})} g, h'\sim^{({\overline{H}})} h} H{\mathfrak{m}}_{g'h'}^{(\overline{H})} \right) \subseteq \beta (H{\mathfrak{m}}_g^{(\overline{H})})\gamma (H) + \beta (H)\gamma (H{\mathfrak{m}}_h^{(\overline{H})}) = 0,\end{equation*}
\begin{equation*} \beta \gamma \left( \bigcap_{g'\sim^{({\overline{H}})} g, h'\sim^{({\overline{H}})} h} H{\mathfrak{m}}_{g'h'}^{(\overline{H})} \right) \subseteq \beta (H{\mathfrak{m}}_g^{(\overline{H})})\gamma (H) + \beta (H)\gamma (H{\mathfrak{m}}_h^{(\overline{H})}) = 0,\end{equation*}
proving part (2) of the proposition.
Let us prove (5.9). By the definition of the coproduct of A,
 \begin{eqnarray*} \Delta\left( \bigcap_{g'\sim^{({\overline{H}})} g, h'\sim^{({\overline{H}})} h} {\mathfrak{m}}_{g'h'} \right) &\subseteq& \bigcap_{g'\sim^{({\overline{H}})} g, h'\sim^{({\overline{H}})} h} \Delta\left( {\mathfrak{m}}_{g'h'}\right)\\ &\subseteq& \bigcap_{g'\sim^{({\overline{H}})} g, h'\sim^{({\overline{H}})} h} ({\mathfrak{m}}_{g'}\otimes A + A\otimes{\mathfrak{m}}_{h'}) =\;:\;I.\end{eqnarray*}
\begin{eqnarray*} \Delta\left( \bigcap_{g'\sim^{({\overline{H}})} g, h'\sim^{({\overline{H}})} h} {\mathfrak{m}}_{g'h'} \right) &\subseteq& \bigcap_{g'\sim^{({\overline{H}})} g, h'\sim^{({\overline{H}})} h} \Delta\left( {\mathfrak{m}}_{g'h'}\right)\\ &\subseteq& \bigcap_{g'\sim^{({\overline{H}})} g, h'\sim^{({\overline{H}})} h} ({\mathfrak{m}}_{g'}\otimes A + A\otimes{\mathfrak{m}}_{h'}) =\;:\;I.\end{eqnarray*}
Thus (5.9) will follow if it can be shown that
![]() $I = J$
. It is clear that
$I = J$
. It is clear that
![]() $J \subseteq I$
. To prove equality, let
$J \subseteq I$
. To prove equality, let
![]() $r=|\mathcal{O}_{{\mathfrak{m}}_g}|$
and
$r=|\mathcal{O}_{{\mathfrak{m}}_g}|$
and
![]() $s=|\mathcal{O}_{{\mathfrak{m}}_h}|$
. Then it follows from
$s=|\mathcal{O}_{{\mathfrak{m}}_h}|$
. Then it follows from
![]() $(\mathbf{{OrbSemi}})$
that
$(\mathbf{{OrbSemi}})$
that
This completes the proof of (5.9).
(4) Since H is orbitally semisimple,
![]() $\left| \mathcal{O}_{{\mathfrak{m}}_g} \right| = \textrm{dim}_k (A/ {\mathfrak{m}}_g^{(\overline{H})})$
by (5.1), hence (4) is (5.3).
$\left| \mathcal{O}_{{\mathfrak{m}}_g} \right| = \textrm{dim}_k (A/ {\mathfrak{m}}_g^{(\overline{H})})$
by (5.1), hence (4) is (5.3).
(5) Since H is orbitally semisimple,
![]() $H/H{\mathfrak{m}}_g^{(\overline{H})} = \bigoplus_{h \sim^{(\overline{H})} g} H/H{\mathfrak{m}}_h$
, so this follows from the definition of
$H/H{\mathfrak{m}}_g^{(\overline{H})} = \bigoplus_{h \sim^{(\overline{H})} g} H/H{\mathfrak{m}}_h$
, so this follows from the definition of
![]() $\widehat{g}$
.
$\widehat{g}$
.
Remark 5.11. The formula (5.8) cannot be further simplified. To see this, consider the group algebra
![]() $H \;:\!=\; kD$
of the dihedral group as in Remark 3.3(1). Recall that
$H \;:\!=\; kD$
of the dihedral group as in Remark 3.3(1). Recall that
![]() $A = \; k[b^{\pm 1}] \; = \; \mathcal{O}(k^{\times}),$
so,
$A = \; k[b^{\pm 1}] \; = \; \mathcal{O}(k^{\times}),$
so,
![]() $G_H = k^{\times}$
. Now
$G_H = k^{\times}$
. Now
![]() $\overline{H} = k\langle a \rangle$
, so the
$\overline{H} = k\langle a \rangle$
, so the
![]() $\overline{H}$
-orbits in
$\overline{H}$
-orbits in
![]() $\textrm{Maxspec}(A)$
are
$\textrm{Maxspec}(A)$
are
and
![]() $\overline{H}^{\ast} \cong \overline{H}.$
Clearly H satisfies both
$\overline{H}^{\ast} \cong \overline{H}.$
Clearly H satisfies both
![]() $(\mathbf{{CoSplit}})$
with
$(\mathbf{{CoSplit}})$
with
![]() $X \;:\!=\; (a-1)kA$
, and
$X \;:\!=\; (a-1)kA$
, and
![]() $(\mathbf{{OrbSemi}})$
, since
$(\mathbf{{OrbSemi}})$
, since
![]() $\overline{H}$
is a group algebra. Therefore, by Propositions 5.9(4) and 5.10(5), and using (5.11),
$\overline{H}$
is a group algebra. Therefore, by Propositions 5.9(4) and 5.10(5), and using (5.11),
and
![]() $\widehat{1}=1\otimes kC_2$
and
$\widehat{1}=1\otimes kC_2$
and
![]() $\widehat{-1}=k\Pi^\circ(\chi_{-1})\otimes kC_2$
. Hence, for
$\widehat{-1}=k\Pi^\circ(\chi_{-1})\otimes kC_2$
. Hence, for
![]() $g,h\in k^\times\setminus\lbrace \pm 1 \rbrace$
,
$g,h\in k^\times\setminus\lbrace \pm 1 \rbrace$
,
Thus the inclusion of (5.8) is an equality in this instance.
5.5 Decomposition of
 $\widehat{kG_H}$
$\widehat{kG_H}$
Before uniting the conclusions of Propositions 5.9 and 5.10 in Theorem 5.13, we need one more lemma. Recall from Section 2.2 and Lemma 3.1 the Hopf surjection
![]() $\iota^{\circ} \;:\;H^{\circ} \longrightarrow A^{\circ}$
, so that
$\iota^{\circ} \;:\;H^{\circ} \longrightarrow A^{\circ}$
, so that
![]() $H^{\circ}$
is a right
$H^{\circ}$
is a right
![]() $A^{\circ}$
-comodule algebra via the map
$A^{\circ}$
-comodule algebra via the map
![]() $\rho \;:\;= ({\textrm{id}} \otimes \iota^{\circ})\circ \Delta$
.
$\rho \;:\;= ({\textrm{id}} \otimes \iota^{\circ})\circ \Delta$
.
Lemma 5.12. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf algebra satisfying
$A \subseteq H$
be an affine commutative-by-finite Hopf algebra satisfying
![]() $(\mathbf{{OrbSemi}})$
. Assume that A is semiprime or central, or that H is pointed. In the notation of Sections 2.2, 5.1, Definition 5.7 and Lemma 3.1, the following hold for each
$(\mathbf{{OrbSemi}})$
. Assume that A is semiprime or central, or that H is pointed. In the notation of Sections 2.2, 5.1, Definition 5.7 and Lemma 3.1, the following hold for each
![]() $g \in G_H$
:
$g \in G_H$
:
-
(1)
 $\qquad \iota^\circ(\widehat{g}) = \bigoplus_{h\sim^{({\overline{H}})} g} k\chi_h$
.
$\qquad \iota^\circ(\widehat{g}) = \bigoplus_{h\sim^{({\overline{H}})} g} k\chi_h$
. -
(2)
 $\qquad \widehat{g} \; \supseteq \; \lbrace f\in H^\circ\;:\;\rho(f) \in f\otimes \sum_{h\sim^{({\overline{H}})} g} k \chi_h \rbrace$
.
$\qquad \widehat{g} \; \supseteq \; \lbrace f\in H^\circ\;:\;\rho(f) \in f\otimes \sum_{h\sim^{({\overline{H}})} g} k \chi_h \rbrace$
. -
(3)
 $\qquad \widehat{1_{G_H}} \; = \; \overline{H}^{\ast}\; = \; \lbrace f\in H^\circ\;:\;\rho(f)=f\otimes 1 \rbrace$
.
$\qquad \widehat{1_{G_H}} \; = \; \overline{H}^{\ast}\; = \; \lbrace f\in H^\circ\;:\;\rho(f)=f\otimes 1 \rbrace$
.
Proof.
-
(1) Let
 $g \in G_H$
and take
$g \in G_H$
and take
 $f\in\widehat{g}$
, so that
$f\in\widehat{g}$
, so that
 $\left.f\right|_A({\mathfrak{m}}_g^{(\overline{H})}) =0$
. Since
$\left.f\right|_A({\mathfrak{m}}_g^{(\overline{H})}) =0$
. Since
 $A \subseteq H$
satisfies
$A \subseteq H$
satisfies
 $(\mathbf{{OrbSemi}})$
the Chinese remainder theorem implies that Conversely, let
$(\mathbf{{OrbSemi}})$
the Chinese remainder theorem implies that Conversely, let \begin{equation*} \iota^{\circ}(f) = \left.f\right|_A\in \left(A/{\mathfrak{m}}_g^{(\overline{H})}\right)^{\ast}\cong \bigoplus_{h\sim^{({\overline{H}})} g}(A/{\mathfrak{m}}_h)^{\ast} = \bigoplus_{h\sim^{({\overline{H}})} g} k\chi_h. \end{equation*}
\begin{equation*} \iota^{\circ}(f) = \left.f\right|_A\in \left(A/{\mathfrak{m}}_g^{(\overline{H})}\right)^{\ast}\cong \bigoplus_{h\sim^{({\overline{H}})} g}(A/{\mathfrak{m}}_h)^{\ast} = \bigoplus_{h\sim^{({\overline{H}})} g} k\chi_h. \end{equation*}
 $\alpha=\sum_{h\sim^{({\overline{H}})} g} \lambda_h\chi_h \in A^{\circ}$
for some
$\alpha=\sum_{h\sim^{({\overline{H}})} g} \lambda_h\chi_h \in A^{\circ}$
for some
 $\lambda_h\in k$
. Then
$\lambda_h\in k$
. Then
 $\alpha=\iota^\circ(\Pi^\circ(\alpha))$
by Lemma 3.1(5). Recall that
$\alpha=\iota^\circ(\Pi^\circ(\alpha))$
by Lemma 3.1(5). Recall that
 $H=A\oplus X$
as right A-modules by (1.1) in Section 1.2. Thus as
$H=A\oplus X$
as right A-modules by (1.1) in Section 1.2. Thus as \begin{equation*} \Pi^\circ(\alpha)(H{\mathfrak{m}}_g^{(\overline{H})}) = \Pi^\circ(\alpha)({\mathfrak{m}}_g^{(\overline{H})}\oplus X{\mathfrak{m}}_g^{(\overline{H})}))= \alpha({\mathfrak{m}}_g^{(\overline{H})}) = \sum_{h\sim^{(\overline{H})} g} \lambda_h\chi_h({\mathfrak{m}}_g^{(\overline{H})})=0, \end{equation*}
\begin{equation*} \Pi^\circ(\alpha)(H{\mathfrak{m}}_g^{(\overline{H})}) = \Pi^\circ(\alpha)({\mathfrak{m}}_g^{(\overline{H})}\oplus X{\mathfrak{m}}_g^{(\overline{H})}))= \alpha({\mathfrak{m}}_g^{(\overline{H})}) = \sum_{h\sim^{(\overline{H})} g} \lambda_h\chi_h({\mathfrak{m}}_g^{(\overline{H})})=0, \end{equation*}
 ${\mathfrak{m}}_g^{(\overline{H})}\subseteq {\mathfrak{m}}_h$
for every
${\mathfrak{m}}_g^{(\overline{H})}\subseteq {\mathfrak{m}}_h$
for every
 $h\sim^{(\overline{H})} g$
. Thus
$h\sim^{(\overline{H})} g$
. Thus
 $\Pi^\circ(\alpha)\in\widehat{g}$
and
$\Pi^\circ(\alpha)\in\widehat{g}$
and
 $\alpha\in\iota^\circ(\widehat{g})$
, proving (1).
$\alpha\in\iota^\circ(\widehat{g})$
, proving (1).
-
(2) Let
 $f \in H^{\circ}$
and suppose
$f \in H^{\circ}$
and suppose
 $\rho(f)=f\otimes \sum_{h\sim^{(\overline{H})} g} \lambda_h \chi_h$
for some
$\rho(f)=f\otimes \sum_{h\sim^{(\overline{H})} g} \lambda_h \chi_h$
for some
 $\lambda_h\in k$
. Then as
$\lambda_h\in k$
. Then as \begin{eqnarray*}f(H{\mathfrak{m}}_g^{(\overline{H})}) &=& \sum f_1(H) f_2({\mathfrak{m}}_g^{(\overline{H})}) = \sum f_1(H) \left.f_2\right|_A ({\mathfrak{m}}_g^{(\overline{H})}) \\&=& \rho(f)(H\otimes {\mathfrak{m}}_g^{(\overline{H})}) = f(H)\left( \sum_{h\sim^{({\overline{H}})} g} \lambda_h \chi_h({\mathfrak{m}}_g^{(\overline{H})}) \right) =0,\end{eqnarray*}
\begin{eqnarray*}f(H{\mathfrak{m}}_g^{(\overline{H})}) &=& \sum f_1(H) f_2({\mathfrak{m}}_g^{(\overline{H})}) = \sum f_1(H) \left.f_2\right|_A ({\mathfrak{m}}_g^{(\overline{H})}) \\&=& \rho(f)(H\otimes {\mathfrak{m}}_g^{(\overline{H})}) = f(H)\left( \sum_{h\sim^{({\overline{H}})} g} \lambda_h \chi_h({\mathfrak{m}}_g^{(\overline{H})}) \right) =0,\end{eqnarray*}
 ${\mathfrak{m}}_g^{(\overline{H})}\subseteq {\mathfrak{m}}_h$
for every
${\mathfrak{m}}_g^{(\overline{H})}\subseteq {\mathfrak{m}}_h$
for every
 $h\sim^{(\overline{H})} g$
. Hence
$h\sim^{(\overline{H})} g$
. Hence
 $f\in \widehat{g}$
.
$f\in \widehat{g}$
.
-
(3) That the left side contains the right is a special case of (2). For the reverse inclusion, let
 $f\in\overline{H}^*=\widehat{1_G}$
. By part (1) say
$f\in\overline{H}^*=\widehat{1_G}$
. By part (1) say \begin{equation*}\rho(f)\in ({\textrm{id}} \otimes \iota^{\circ})(\overline{H}^* \otimes \overline{H}^*) = \overline{H}^*\otimes k \varepsilon_A, \end{equation*}
\begin{equation*}\rho(f)\in ({\textrm{id}} \otimes \iota^{\circ})(\overline{H}^* \otimes \overline{H}^*) = \overline{H}^*\otimes k \varepsilon_A, \end{equation*}
 $\rho(f)=f'\otimes \varepsilon_A$
for some
$\rho(f)=f'\otimes \varepsilon_A$
for some
 $f'\in\overline{H}^*$
. By the counit axiom of right comodules,
$f'\in\overline{H}^*$
. By the counit axiom of right comodules,
 $f=\varepsilon_A(1_A)f'=f'$
, hence
$f=\varepsilon_A(1_A)f'=f'$
, hence
 $\rho(f)=f\otimes 1_{A^\circ}$
, proving (3).
$\rho(f)=f\otimes 1_{A^\circ}$
, proving (3).
We can now show that when
![]() $A \subseteq H$
satisfies
$A \subseteq H$
satisfies
![]() $(\mathbf{{OrbSemi}})$
$(\mathbf{{OrbSemi}})$
![]() $\widehat{kG_H}$
decomposes as a crossed or smash product whenever
$\widehat{kG_H}$
decomposes as a crossed or smash product whenever
![]() $H^{\circ}$
does, generalising the presence of the group algebra
$H^{\circ}$
does, generalising the presence of the group algebra
![]() $kG_H$
in the dual of a commutative semiprime Hopf algebra.
$kG_H$
in the dual of a commutative semiprime Hopf algebra.
Theorem 5.13. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf algebra satisfying
$A \subseteq H$
be an affine commutative-by-finite Hopf algebra satisfying
![]() $(\mathbf{{OrbSemi}})$
, and assume that A is semiprime or central, or that H is pointed.
$(\mathbf{{OrbSemi}})$
, and assume that A is semiprime or central, or that H is pointed.
-
(1) Suppose that
 $H^{\circ}\cong \overline{H}^{\ast}\#_\sigma A^{\circ}$
decomposes as a crossed product for some cocycle
$H^{\circ}\cong \overline{H}^{\ast}\#_\sigma A^{\circ}$
decomposes as a crossed product for some cocycle
 $\sigma$
and action of
$\sigma$
and action of
 $A^{\circ}$
on
$A^{\circ}$
on
 $\overline{H}^*$
. Then (5.13)as algebras, left
$\overline{H}^*$
. Then (5.13)as algebras, left \begin{equation} \widehat{kG_H}\; \cong \; \overline{H}^* \#_{\left.\sigma\right|_{kG_H \otimes kG_H}} kG_H\end{equation}
\begin{equation} \widehat{kG_H}\; \cong \; \overline{H}^* \#_{\left.\sigma\right|_{kG_H \otimes kG_H}} kG_H\end{equation}
 $\overline{H}^{\ast}$
-modules and right
$\overline{H}^{\ast}$
-modules and right
 $kG_H$
-comodules.
$kG_H$
-comodules.
-
(2) Suppose
 $A \subseteq H$
satisfies
$A \subseteq H$
satisfies
 $(\mathbf{{CoSplit}})$
. Then, in (5.13),
$(\mathbf{{CoSplit}})$
. Then, in (5.13),
 $\sigma$
is trivial, so
$\sigma$
is trivial, so
 $\widehat{kG_H}$
is a smash product of
$\widehat{kG_H}$
is a smash product of
 $\overline{H}^{\ast}$
by
$\overline{H}^{\ast}$
by
 $\widetilde{G_H}$
, (5.14)with action given, for
$\widetilde{G_H}$
, (5.14)with action given, for \begin{equation} \widehat{kG_H} \; = \; \overline{H}^* \# k\widetilde{G_H},\end{equation}
\begin{equation} \widehat{kG_H} \; = \; \overline{H}^* \# k\widetilde{G_H},\end{equation}
 $g\in G_H, \varphi\in\overline{H}^*$
, by
$g\in G_H, \varphi\in\overline{H}^*$
, by  \begin{equation*} \Pi^{\circ}(\chi_g)\cdot \varphi = \Pi^\circ(\chi_g)\varphi\Pi^\circ(\chi_{g^{-1}}). \end{equation*}
\begin{equation*} \Pi^{\circ}(\chi_g)\cdot \varphi = \Pi^\circ(\chi_g)\varphi\Pi^\circ(\chi_{g^{-1}}). \end{equation*}
Proof.
-
(1) Suppose that
 $H^\circ\cong \overline{H}^* \#_\sigma A^\circ$
. By [Reference Doi and Takeuchi14] (see Remark 2.3(4)), there exists a convolution invertible right
$H^\circ\cong \overline{H}^* \#_\sigma A^\circ$
. By [Reference Doi and Takeuchi14] (see Remark 2.3(4)), there exists a convolution invertible right
 $A^\circ$
-comodule map
$A^\circ$
-comodule map
 $\gamma:A^\circ\to H^\circ$
such that the isomorphism is given by
$\gamma:A^\circ\to H^\circ$
such that the isomorphism is given by
 $f\# \varphi\mapsto f\gamma(\varphi)$
. The core of this proof is showing that (5.15)We first claim that
$f\# \varphi\mapsto f\gamma(\varphi)$
. The core of this proof is showing that (5.15)We first claim that \begin{equation} \widehat{g}=\bigoplus_{h\sim^{(\overline{H})} g} \overline{H}^*\gamma(\chi_h). \end{equation}
\begin{equation} \widehat{g}=\bigoplus_{h\sim^{(\overline{H})} g} \overline{H}^*\gamma(\chi_h). \end{equation}
 $\gamma(\chi_h)\in\widehat{g}$
. Since
$\gamma(\chi_h)\in\widehat{g}$
. Since
 $\gamma:A^\circ\to H^\circ$
is a right
$\gamma:A^\circ\to H^\circ$
is a right
 $A^\circ$
-comodule map and
$A^\circ$
-comodule map and
 $\chi_h$
is a grouplike element of
$\chi_h$
is a grouplike element of
 $A^{\circ}$
, then and the claim follows from Lemma 5.12(2). Therefore, by Proposition 5.10(3)
$A^{\circ}$
, then and the claim follows from Lemma 5.12(2). Therefore, by Proposition 5.10(3) \begin{equation*} \rho\gamma(\chi_h) = (\gamma\otimes {\textrm{id}})\Delta_{A}(\chi_h) = \gamma(\chi_h)\otimes \chi_h \end{equation*}
proving the inclusion of the right of (5.15) in the left. For the reverse inclusion, let
\begin{equation*} \rho\gamma(\chi_h) = (\gamma\otimes {\textrm{id}})\Delta_{A}(\chi_h) = \gamma(\chi_h)\otimes \chi_h \end{equation*}
proving the inclusion of the right of (5.15) in the left. For the reverse inclusion, let \begin{equation*} \overline{H}^*\gamma(\chi_h) \subseteq \overline{H}^*\widehat{g}\subseteq \widehat{g}, \end{equation*}
\begin{equation*} \overline{H}^*\gamma(\chi_h) \subseteq \overline{H}^*\widehat{g}\subseteq \widehat{g}, \end{equation*}
 $f\in\widehat{g}$
. By the second sentence of the proof,
$f\in\widehat{g}$
. By the second sentence of the proof,
 $f=\sum_{i=1}^n f_i\gamma(u_i\#\chi_{g_i})$
, where
$f=\sum_{i=1}^n f_i\gamma(u_i\#\chi_{g_i})$
, where
 $f_i\in\overline{H}^*, u_i\in U(\mathfrak{g}), g_i\in G_H$
. Since
$f_i\in\overline{H}^*, u_i\in U(\mathfrak{g}), g_i\in G_H$
. Since
 $\rho$
is an algebra homomorphism and
$\rho$
is an algebra homomorphism and
 $\gamma:A^\circ\to H^\circ$
is a right
$\gamma:A^\circ\to H^\circ$
is a right
 $A^\circ$
-comodule map, and since
$A^\circ$
-comodule map, and since
 $\chi_{g_i} \in A^{\circ}$
is grouplike and
$\chi_{g_i} \in A^{\circ}$
is grouplike and
 $\rho(f_i)=f_i\otimes 1$
by Lemma 5.12(2) we have But by Lemma 5.12(1)
$\rho(f_i)=f_i\otimes 1$
by Lemma 5.12(2) we have But by Lemma 5.12(1) \begin{eqnarray*}\rho(f) &=& \sum_{i=1}^n \rho(f_i)\rho\gamma(u_i\#\chi_{g_i}) = \sum_{i=1}^n \rho(f_i) (\gamma\otimes {\textrm{id}})\Delta(u_i\#\chi_{g_i}) \\&=& \sum_{i=1}^n \sum_{(u_i)} f_i\gamma(u_{i,1}\#\chi_{g_i})\otimes (u_{i,2}\#\chi_{g_i}).\end{eqnarray*}
Moreover, since each
\begin{eqnarray*}\rho(f) &=& \sum_{i=1}^n \rho(f_i)\rho\gamma(u_i\#\chi_{g_i}) = \sum_{i=1}^n \rho(f_i) (\gamma\otimes {\textrm{id}})\Delta(u_i\#\chi_{g_i}) \\&=& \sum_{i=1}^n \sum_{(u_i)} f_i\gamma(u_{i,1}\#\chi_{g_i})\otimes (u_{i,2}\#\chi_{g_i}).\end{eqnarray*}
Moreover, since each \begin{equation*} \rho(f)\in \widehat{g}\otimes\iota^\circ(\widehat{g})=\bigoplus_{h\sim^{(\overline{H})} g} \widehat{g}\otimes \chi_h.\end{equation*}
\begin{equation*} \rho(f)\in \widehat{g}\otimes\iota^\circ(\widehat{g})=\bigoplus_{h\sim^{(\overline{H})} g} \widehat{g}\otimes \chi_h.\end{equation*}
 $u_i$
is a polynomial on primitive elements, we must have
$u_i$
is a polynomial on primitive elements, we must have
 $g_i\sim^{(\overline{H})} g$
for every i, and each
$g_i\sim^{(\overline{H})} g$
for every i, and each
 $u_i=1$
. Hence f has the required form, and (5.15) follows. Therefore, as vector spaces, left
$u_i=1$
. Hence f has the required form, and (5.15) follows. Therefore, as vector spaces, left \begin{equation*} \widehat{kG_H} = \overline{H}^*\gamma(kG_H) \cong \overline{H}^*\otimes kG_H \end{equation*}
\begin{equation*} \widehat{kG_H} = \overline{H}^*\gamma(kG_H) \cong \overline{H}^*\otimes kG_H \end{equation*}
 $\overline{H}^*$
-modules and right
$\overline{H}^*$
-modules and right
 $kG_H$
-comodules, since by the calculations above
$kG_H$
-comodules, since by the calculations above
 $\rho(\widehat{kG_H})\subseteq \widehat{kG_H}\otimes kG_H$
, that is the
$\rho(\widehat{kG_H})\subseteq \widehat{kG_H}\otimes kG_H$
, that is the
 $A^\circ$
-comodule structure of
$A^\circ$
-comodule structure of
 $H^\circ$
restricts to a
$H^\circ$
restricts to a
 $kG_H$
-comodule structure for
$kG_H$
-comodule structure for
 $\widehat{kG_H}$
. In particular, by Lemma 3.1 Also, since
$\widehat{kG_H}$
. In particular, by Lemma 3.1 Also, since \begin{equation*} \widehat{kG_H}^{co\, kG_H} = \widehat{kG_H}\cap (H^\circ)^{co\,A^\circ} = \widehat{kG_H}\cap\overline{H}^* = \overline{H}^*. \end{equation*}
\begin{equation*} \widehat{kG_H}^{co\, kG_H} = \widehat{kG_H}\cap (H^\circ)^{co\,A^\circ} = \widehat{kG_H}\cap\overline{H}^* = \overline{H}^*. \end{equation*}
 $\gamma\;:\;A^\circ\to H^\circ$
is convolution invertible, then so is its restriction to the coradical
$\gamma\;:\;A^\circ\to H^\circ$
is convolution invertible, then so is its restriction to the coradical
 $\left.\gamma\right|_{kG_H}:\;kG_H\to \widehat{kG_H}$
, [Reference Takeuchi35, Lemma 14]. Therefore, and by inspecting the formulae for the cocyles
$\left.\gamma\right|_{kG_H}:\;kG_H\to \widehat{kG_H}$
, [Reference Takeuchi35, Lemma 14]. Therefore, and by inspecting the formulae for the cocyles \begin{equation*} \widehat{kG_H} \cong \overline{H}^* \#_\tau kG_H \end{equation*}
\begin{equation*} \widehat{kG_H} \cong \overline{H}^* \#_\tau kG_H \end{equation*}
 $\sigma$
and
$\sigma$
and
 $\tau$
one easily sees that
$\tau$
one easily sees that
 $\tau=\left.\sigma\right|_{kG_H\otimes kG_H}$
.
$\tau=\left.\sigma\right|_{kG_H\otimes kG_H}$
.
-
(2) If X can be chosen to be a coideal, then
 $H^\circ\cong \overline{H}^* \# A^\circ$
by Theorem 3.2(1), hence the cocycle
$H^\circ\cong \overline{H}^* \# A^\circ$
by Theorem 3.2(1), hence the cocycle
 $\sigma$
is trivial and
$\sigma$
is trivial and
 $\widehat{kG_H}$
decomposes as a smash product. The action of
$\widehat{kG_H}$
decomposes as a smash product. The action of
 $kG_H$
on
$kG_H$
on
 $\overline{H}^*$
is a special case of Remark 3.3(2).
$\overline{H}^*$
is a special case of Remark 3.3(2).
6.
 $H^{\circ}$
under the auspices of (CoSplit) and (OrbSemi)
$H^{\circ}$
under the auspices of (CoSplit) and (OrbSemi)
Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf algebra. Recall that the subspaces
$A \subseteq H$
be an affine commutative-by-finite Hopf algebra. Recall that the subspaces
![]() $W(H^{\circ})$
and
$W(H^{\circ})$
and
![]() $\widehat{kG_H}$
of
$\widehat{kG_H}$
of
![]() $H^\circ$
were introduced in Definitions 4.1 and 5.7. In the presence of
$H^\circ$
were introduced in Definitions 4.1 and 5.7. In the presence of
![]() $(\mathbf{{CoSplit}})$
and
$(\mathbf{{CoSplit}})$
and
![]() $(\mathbf{{OrbSemi}})$
, one has for
$(\mathbf{{OrbSemi}})$
, one has for
![]() $H^{\circ}$
the following generalisation of the description of the Hopf dual of a commutative Hopf algebra via the Cartier–Gabriel–Kostant theorem.
$H^{\circ}$
the following generalisation of the description of the Hopf dual of a commutative Hopf algebra via the Cartier–Gabriel–Kostant theorem.
Theorem 6.1. Let
![]() $A \subseteq H$
be an affine commutative-by-finite Hopf algebra and assume that A is semiprime or central, or that H is pointed. Suppose that
$A \subseteq H$
be an affine commutative-by-finite Hopf algebra and assume that A is semiprime or central, or that H is pointed. Suppose that
![]() $A \subseteq H$
satisfies
$A \subseteq H$
satisfies
![]() $(\mathbf{{CoSplit}})$
and
$(\mathbf{{CoSplit}})$
and
![]() $(\mathbf{{OrbSemi}})$
. Retain the notation of Sections 2.2, 3.1 and of Definitions 4.1 and 5.7.
$(\mathbf{{OrbSemi}})$
. Retain the notation of Sections 2.2, 3.1 and of Definitions 4.1 and 5.7.
-
(1)
 $H^\circ$
is a smash product (6.1)where
$H^\circ$
is a smash product (6.1)where \begin{equation}H^\circ \;\cong \; \overline{H}^\ast \#\, A^\circ \; \cong \; (\overline{H}^\ast \# \,A')\# kG_H,\end{equation}
\begin{equation}H^\circ \;\cong \; \overline{H}^\ast \#\, A^\circ \; \cong \; (\overline{H}^\ast \# \,A')\# kG_H,\end{equation}
 $A/N(A) = \mathcal{O}(G_H)$
, where N(A) is the nilradical of A. If
$A/N(A) = \mathcal{O}(G_H)$
, where N(A) is the nilradical of A. If
 $\textrm{char}k = 0$
then
$\textrm{char}k = 0$
then
 $A' = U(\mathfrak{g})$
, where
$A' = U(\mathfrak{g})$
, where
 $\mathfrak{g}$
is the Lie algebra of
$\mathfrak{g}$
is the Lie algebra of
 $G_H$
.
$G_H$
.
-
(2)
 $H^\circ$
contains three Hopf subalgebras:
$H^\circ$
contains three Hopf subalgebras:
 $\overline{H}^\ast$
, (6.2)and
$\overline{H}^\ast$
, (6.2)and \begin{equation}W(H^\circ) \; \cong \; \overline{H}^\ast \#\, A'\end{equation}
(6.3)with
\begin{equation}W(H^\circ) \; \cong \; \overline{H}^\ast \#\, A'\end{equation}
(6.3)with \begin{equation}\widehat{kG_H}\; \cong \; \overline{H}^\ast \#\, kG_H,\end{equation}
\begin{equation}\widehat{kG_H}\; \cong \; \overline{H}^\ast \#\, kG_H,\end{equation}
 $A' \cong U(\mathfrak{g})$
if k has characteristic 0.
$A' \cong U(\mathfrak{g})$
if k has characteristic 0.
-
(3) Suppose that
 $\overline{H}$
is semisimple and k has characteristic 0. Then the action of
$\overline{H}$
is semisimple and k has characteristic 0. Then the action of
 $U(\mathfrak{g})$
on
$U(\mathfrak{g})$
on
 $\overline{H}$
is inner, so that (6.4)a skew group algebra with coefficient ring the Hopf subalgebra
$\overline{H}$
is inner, so that (6.4)a skew group algebra with coefficient ring the Hopf subalgebra \begin{equation} H^{\circ} \; \cong \; (\overline{H}^{\ast} \otimes U(\mathfrak{g})) \# kG_H,\end{equation}
\begin{equation} H^{\circ} \; \cong \; (\overline{H}^{\ast} \otimes U(\mathfrak{g})) \# kG_H,\end{equation}
 $W(H^{\circ})$
.
$W(H^{\circ})$
.
Proof. (1),(2) By the isomorphism (3.1) in Section 3.1, there is a decomposition
with A
′ and
![]() $kG_H$
Hopf subalgebras of
$kG_H$
Hopf subalgebras of
![]() $A^{\circ}$
. Substituting (6.5) into the isomorphism (3.8) of Theorem 3.2(1) shows that, as algebras,
$A^{\circ}$
. Substituting (6.5) into the isomorphism (3.8) of Theorem 3.2(1) shows that, as algebras,
More precisely, the proof of Theorem 3.2(1), using the fact that
![]() $\Pi^{\circ}$
is an algebra homomorphism, shows that we can rewrite (6.6) as
$\Pi^{\circ}$
is an algebra homomorphism, shows that we can rewrite (6.6) as
From (6.7), by Theorem 4.3(2),(5) and their proofs,
![]() $H^{\circ}$
contains as a normal Hopf subalgebra the smash product
$H^{\circ}$
contains as a normal Hopf subalgebra the smash product
Moreover, by Proposition 5.9(3),
![]() $H^{\circ} = \overline{H}^{\ast} \# \Pi^{\circ}(A' \# kG_H)$
contains the skew group algebra
$H^{\circ} = \overline{H}^{\ast} \# \Pi^{\circ}(A' \# kG_H)$
contains the skew group algebra
and this equals the Hopf subalgebra
![]() $\widehat{kG_H}$
of
$\widehat{kG_H}$
of
![]() $H^{\circ}$
thanks to the equality (5.14) of Theorem 5.13.
$H^{\circ}$
thanks to the equality (5.14) of Theorem 5.13.
(3) This is Corollary 4.4 combined with parts (1) and (2).
Remark 6.2. (1) For the record, we state explicitly here the question about our standing hypotheses already mentioned in Section 1.3.
Question 6.3. Let H be an affine commutative-by-finite Hopf algebra. Is there always a choice of normal commutative Hopf subalgebra A of H such that
![]() $A \subseteq H$
satisfies
$A \subseteq H$
satisfies
![]() $(\mathbf{{CoSplit}})$
and
$(\mathbf{{CoSplit}})$
and
![]() $(\mathbf{{OrbSemi}})$
?
$(\mathbf{{OrbSemi}})$
?
We review the status of this question for a large number of families of examples in Section 7.
(2) The smash product decompositions in Theorem 6.1 in general have nontrivial actions. For example, the actions in (6.2) and (6.3) are nontrivial for
![]() $H=B(n,w,q)$
defined in Section 7.5, see Proposition 7.2(IV) and Remarks 7.1(2), with the references given there; and the skew group action in (6.1) is in general nontrivial even when
$H=B(n,w,q)$
defined in Section 7.5, see Proposition 7.2(IV) and Remarks 7.1(2), with the references given there; and the skew group action in (6.1) is in general nontrivial even when
![]() $H = A$
is commutative - for example, the algebra structure of
$H = A$
is commutative - for example, the algebra structure of
![]() $\mathcal{O}(G)^{\circ}$
when G is a semidirect product of
$\mathcal{O}(G)^{\circ}$
when G is a semidirect product of
![]() $(k,+)$
by
$(k,+)$
by
![]() $k^{\times}$
is determined in [Reference Couto11, Appendix A.4].
$k^{\times}$
is determined in [Reference Couto11, Appendix A.4].
7. Examples
We list here a number of classes of examples of affine commutative-by-finite Hopf algebras and discuss in each case what our results tell us about their Hopf duals.
7.1 Enveloping algebras of Lie algebras in positive characteristic
Assume that k has positive characteristic p. Let
![]() $\mathfrak{g}$
be a k-Lie algebra with basis
$\mathfrak{g}$
be a k-Lie algebra with basis
![]() $\{x_1, \ldots , x_n\}$
. Then
$\{x_1, \ldots , x_n\}$
. Then
![]() $H \;:\!=\; U(\mathfrak{g})$
is a free module of finite rank over a central polynomial Hopf subalgebra
$H \;:\!=\; U(\mathfrak{g})$
is a free module of finite rank over a central polynomial Hopf subalgebra
where each
![]() $y_i$
is a p-polynomial in
$y_i$
is a p-polynomial in
![]() $x_i$
and hence is primitive; see [Reference Jacobson18, Proposition 1]. When
$x_i$
and hence is primitive; see [Reference Jacobson18, Proposition 1]. When
![]() $\mathfrak{g}$
is restricted, with restriction map
$\mathfrak{g}$
is restricted, with restriction map
![]() $x\mapsto x^{[p]}$
, one takes
$x\mapsto x^{[p]}$
, one takes
![]() $y_i \;:\!=\; x_i^p - x_i^{[p]}$
for all i, and in this case the Hopf quotient
$y_i \;:\!=\; x_i^p - x_i^{[p]}$
for all i, and in this case the Hopf quotient
![]() $\overline{H}$
is the restricted enveloping algebra of
$\overline{H}$
is the restricted enveloping algebra of
![]() $\mathfrak{g}$
, usually denoted by
$\mathfrak{g}$
, usually denoted by
![]() $u^{[p]}(\mathfrak{g})$
, with
$u^{[p]}(\mathfrak{g})$
, with
![]() $\textrm{dim}_k (u^{[p]}(\mathfrak{g})) = p^n$
. In the non-restricted case, it is still the case by [Reference Jacobson18, Proposition 2] that
$\textrm{dim}_k (u^{[p]}(\mathfrak{g})) = p^n$
. In the non-restricted case, it is still the case by [Reference Jacobson18, Proposition 2] that
![]() $U(\mathfrak{g})$
is a free A-module, with basis
$U(\mathfrak{g})$
is a free A-module, with basis
where
![]() $y_i$
is a linear combination of
$y_i$
is a linear combination of
![]() $x_{i}^{p^j}$
for
$x_{i}^{p^j}$
for
![]() $j = 0, \ldots , d_i$
. Thus, in the general non-restricted case,
$j = 0, \ldots , d_i$
. Thus, in the general non-restricted case,
Since A is central
![]() $(\mathbf{{OrbSemi}})$
is trivially true for
$(\mathbf{{OrbSemi}})$
is trivially true for
![]() $H = U(\mathfrak{g})$
. Moreover it is clear from (7.1) that, as an A-module complement to A in H, we can choose
$H = U(\mathfrak{g})$
. Moreover it is clear from (7.1) that, as an A-module complement to A in H, we can choose
Thus X is a coideal of H and so
![]() $(\mathbf{{CoSplit}})$
is also valid. We can therefore apply Theorem 6.1(1). Note that
$(\mathbf{{CoSplit}})$
is also valid. We can therefore apply Theorem 6.1(1). Note that
and that
![]() $H^{\circ}$
is commutative since H is cocommutative, so that the actions in the smash products composing
$H^{\circ}$
is commutative since H is cocommutative, so that the actions in the smash products composing
![]() $H^{\circ}$
are all trivial. We conclude that, as algebras,
$H^{\circ}$
are all trivial. We conclude that, as algebras,
with
![]() $\overline{H}^{\ast}$
,
$\overline{H}^{\ast}$
,
![]() $W(H^{\circ}) \, \;:\!=\; \, A' \otimes \overline{H}^{\ast}$
and
$W(H^{\circ}) \, \;:\!=\; \, A' \otimes \overline{H}^{\ast}$
and
![]() $\widehat{k(k,+)^n}\, \;:\!=\; \, \overline{H}^{\ast} \otimes k(k,+)^n$
each being a Hopf subalgebra of
$\widehat{k(k,+)^n}\, \;:\!=\; \, \overline{H}^{\ast} \otimes k(k,+)^n$
each being a Hopf subalgebra of
![]() $U(\mathfrak{g})^{\circ}$
. Here, as an algebra, A
′ is a divided powers algebra in n variables,
$U(\mathfrak{g})^{\circ}$
. Here, as an algebra, A
′ is a divided powers algebra in n variables,
as defined and discussed at [Reference Montgomery26, Examples 5.6.8 and 9.1.7]. Modulo the Hopf ideal
![]() $(\overline{H}^{\ast})^+ A'$
of
$(\overline{H}^{\ast})^+ A'$
of
![]() $W(H^{\circ})$
the coproducts of the elements of A
′ take their classical cocommutative forms. Similarly, the elements of
$W(H^{\circ})$
the coproducts of the elements of A
′ take their classical cocommutative forms. Similarly, the elements of
![]() $(k,+)^n$
are group-like modulo
$(k,+)^n$
are group-like modulo
![]() $(\overline{H}^{\ast})^+k(k,+)^n$
.
$(\overline{H}^{\ast})^+k(k,+)^n$
.
7.2 Group algebras of finitely generated abelian-by-finite groups
Let G be a finitely generated group with an abelian normal subgroup N of finite index. For convenience, we may as well choose N to be torsion free, and hence free abelian of rank n, say. With
![]() $H \;:\!=\; kG$
and
$H \;:\!=\; kG$
and
![]() $A\;:\!=\; kN$
,
$A\;:\!=\; kN$
,
![]() $\overline{H} = k(G/N)$
. Clearly H is a free A-module with basis a set of coset representatives of N in G, and we can choose as a complement to A in H the free A-submodule X with basis the non-trivial coset representatives. Thus X is a subcoalgebra of H, so
$\overline{H} = k(G/N)$
. Clearly H is a free A-module with basis a set of coset representatives of N in G, and we can choose as a complement to A in H the free A-submodule X with basis the non-trivial coset representatives. Thus X is a subcoalgebra of H, so
![]() $(\mathbf{{CoSplit}})$
holds, and
$(\mathbf{{CoSplit}})$
holds, and
![]() $(\mathbf{{OrbSemi}})$
holds since the adjoint action on A is by the group
$(\mathbf{{OrbSemi}})$
holds since the adjoint action on A is by the group
![]() $G/N$
. Thus once again Theorem 6.1(1) applies, and again the smash products occurring are trivial because
$G/N$
. Thus once again Theorem 6.1(1) applies, and again the smash products occurring are trivial because
![]() $H^{\circ}$
is commutative. We deduce that, as algebras,
$H^{\circ}$
is commutative. We deduce that, as algebras,
with
and
![]() $\overline{H}^{\ast}$
,
$\overline{H}^{\ast}$
,
![]() $W(H^{\circ}) \,\;:\!=\; \, k[z_1, \ldots , z_n] \otimes \overline{H}^{\ast}$
and
$W(H^{\circ}) \,\;:\!=\; \, k[z_1, \ldots , z_n] \otimes \overline{H}^{\ast}$
and
![]() $\widehat{k((k^{\times})^n)} \, \;:\!=\; \, \overline{H}^{\ast} \otimes k((k^{\times})^n)$
each being a Hopf subalgebra of
$\widehat{k((k^{\times})^n)} \, \;:\!=\; \, \overline{H}^{\ast} \otimes k((k^{\times})^n)$
each being a Hopf subalgebra of
![]() $kG^{\circ}$
. As in Section 7.1, the elements
$kG^{\circ}$
. As in Section 7.1, the elements
![]() $z_i$
are primitive modulo
$z_i$
are primitive modulo
![]() $(\overline{H}^{\ast})^+k[z_1, \ldots , z_n]$
and the elements of
$(\overline{H}^{\ast})^+k[z_1, \ldots , z_n]$
and the elements of
![]() $(k^{\times})^n$
are group-like modulo
$(k^{\times})^n$
are group-like modulo
![]() $(\overline{H}^{\ast})^+k((k^{\times})^n)$
.
$(\overline{H}^{\ast})^+k((k^{\times})^n)$
.
7.3 Quantized coordinate rings at a root of unity
In this subsection and the next, we assume that
![]() $k = \mathbb{C}$
and that
$k = \mathbb{C}$
and that
![]() $\ell$
is an odd positive integer with
$\ell$
is an odd positive integer with
![]() $\ell \geq 3$
, and prime to 3 if
$\ell \geq 3$
, and prime to 3 if
![]() $\mathfrak{g}$
contains a factor of type
$\mathfrak{g}$
contains a factor of type
![]() $G_2$
. The quantized coordinate ring
$G_2$
. The quantized coordinate ring
![]() $\mathcal{O}_q(G)$
of a connected, simply connected, semisimple Lie group G is a noetherian Hopf algebra, [Reference De Concini and Lyubashenko9, Sections 4.1 and 6.1]. If
$\mathcal{O}_q(G)$
of a connected, simply connected, semisimple Lie group G is a noetherian Hopf algebra, [Reference De Concini and Lyubashenko9, Sections 4.1 and 6.1]. If
![]() $q=\epsilon$
is a primitive
$q=\epsilon$
is a primitive
![]() $\ell$
th root of unity,
$\ell$
th root of unity,
![]() $\mathcal{O}_\epsilon(G)$
is a finite module over a central Hopf subalgebra isomorphic to
$\mathcal{O}_\epsilon(G)$
is a finite module over a central Hopf subalgebra isomorphic to
![]() $\mathcal{O}(G)$
, [Reference De Concini and Lyubashenko9, Proposition 6.4], [Reference Brown and Goodearl4, Theorem III.7.2]. Thus
$\mathcal{O}(G)$
, [Reference De Concini and Lyubashenko9, Proposition 6.4], [Reference Brown and Goodearl4, Theorem III.7.2]. Thus
is an affine commutative-by-finite Hopf algebra which satisfies
![]() $(\mathbf{{OrbSemi}})$
because of the centrality of A. In fact, the extension
$(\mathbf{{OrbSemi}})$
because of the centrality of A. In fact, the extension
![]() $\mathcal{O}(G)\subseteq \mathcal{O}_\epsilon(G)$
is cleft in the sense of Remark 2.3(3), as is noted in [Reference Andruskiewitsch and Andrés-Garcia1, Remark 2.18(b)]), with a cleaving map which is a coalgebra map, as shown in the proof of [Reference Andruskiewitsch and Andrés-Garcia1, Proposition 2.8(c)]. Thus,
$\mathcal{O}(G)\subseteq \mathcal{O}_\epsilon(G)$
is cleft in the sense of Remark 2.3(3), as is noted in [Reference Andruskiewitsch and Andrés-Garcia1, Remark 2.18(b)]), with a cleaving map which is a coalgebra map, as shown in the proof of [Reference Andruskiewitsch and Andrés-Garcia1, Proposition 2.8(c)]. Thus,
![]() $(\mathbf{{CoSplit}})$
is satisfied. The finite-dimensional Hopf quotient
$(\mathbf{{CoSplit}})$
is satisfied. The finite-dimensional Hopf quotient
![]() $\overline{H} \;:\!=\;\mathcal{O}_\epsilon(G)/\mathcal{O}(G)^+\mathcal{O}_\epsilon(G)$
is the restricted quantized coordinate ring, sometimes denoted by
$\overline{H} \;:\!=\;\mathcal{O}_\epsilon(G)/\mathcal{O}(G)^+\mathcal{O}_\epsilon(G)$
is the restricted quantized coordinate ring, sometimes denoted by
![]() $o_\epsilon(G)$
; its vector space dimension is
$o_\epsilon(G)$
; its vector space dimension is
![]() $\ell^{\textrm{dim}(G)}$
. Each of
$\ell^{\textrm{dim}(G)}$
. Each of
![]() $u_{\epsilon}(\mathfrak{g})$
, (defined in Section 7.4), and
$u_{\epsilon}(\mathfrak{g})$
, (defined in Section 7.4), and
![]() $o_{\epsilon}(G)$
is the Hopf dual of the other by [Reference Brown and Goodearl4, Theorem III.7.10]. Thus Theorem 3.2(2) applies, yielding the isomorphism of algebras, left
$o_{\epsilon}(G)$
is the Hopf dual of the other by [Reference Brown and Goodearl4, Theorem III.7.10]. Thus Theorem 3.2(2) applies, yielding the isomorphism of algebras, left
![]() $u_\epsilon(\mathfrak{g})$
-modules and right
$u_\epsilon(\mathfrak{g})$
-modules and right
![]() $U(\mathfrak{g})\#kG$
-comodules
$U(\mathfrak{g})\#kG$
-comodules
where
![]() $\mathfrak{g}=\textrm{Lie } G$
denotes the Lie algebra of G and
$\mathfrak{g}=\textrm{Lie } G$
denotes the Lie algebra of G and
![]() $u_{\epsilon}(\mathfrak{g})$
is
$u_{\epsilon}(\mathfrak{g})$
is
![]() $\overline{U_{\epsilon}(\mathfrak{g})}$
, as defined in Section 7.4. By Theorems 6.1(1), 4.3(5), and 5.13(2),
$\overline{U_{\epsilon}(\mathfrak{g})}$
, as defined in Section 7.4. By Theorems 6.1(1), 4.3(5), and 5.13(2),
![]() $\mathcal{O}_{\epsilon}(G)$
contains the Hopf subalgebras
$\mathcal{O}_{\epsilon}(G)$
contains the Hopf subalgebras
![]() $u_\epsilon(\mathfrak{g})$
,
$u_\epsilon(\mathfrak{g})$
,
and
and the tensorand
![]() $U(\mathfrak{g})\# kG$
on the right of (7.2) is isomorphic to
$U(\mathfrak{g})\# kG$
on the right of (7.2) is isomorphic to
![]() $\mathcal{O}(G)^{\circ}$
as an algebra.
$\mathcal{O}(G)^{\circ}$
as an algebra.
7.4 Quantized enveloping algebras at a root of unity
The quantized enveloping algebra
![]() $U_q(\mathfrak{g})$
of a semisimple finite-dimensional Lie algebra
$U_q(\mathfrak{g})$
of a semisimple finite-dimensional Lie algebra
![]() $\mathfrak{g}$
is a noetherian Hopf algebra [Reference De Concini, Procesi, (Zampieri and D’Agnolo10, Section 9.1], [Reference Chari and Pressley7, Section 9.1A]. When
$\mathfrak{g}$
is a noetherian Hopf algebra [Reference De Concini, Procesi, (Zampieri and D’Agnolo10, Section 9.1], [Reference Chari and Pressley7, Section 9.1A]. When
![]() $q=\epsilon$
is a primitive
$q=\epsilon$
is a primitive
![]() $\ell$
th root of unity
$\ell$
th root of unity
![]() $U_\epsilon(\mathfrak{g})$
is a free module of rank
$U_\epsilon(\mathfrak{g})$
is a free module of rank
![]() $\ell^{\dim_k(\mathfrak{g})}$
over a central Hopf domain A [Reference De Concini, Procesi, (Zampieri and D’Agnolo10, Corollary and Theorem 19.1], [Reference Brown and Goodearl4, Theorem III.6.2]. The Hopf subalgebra A is the coordinate ring of a certain solvable Poisson algebraic group T with
$\ell^{\dim_k(\mathfrak{g})}$
over a central Hopf domain A [Reference De Concini, Procesi, (Zampieri and D’Agnolo10, Corollary and Theorem 19.1], [Reference Brown and Goodearl4, Theorem III.6.2]. The Hopf subalgebra A is the coordinate ring of a certain solvable Poisson algebraic group T with
![]() $\textrm{dim}T = \textrm{dim}_k(\mathfrak{g})$
; see [Reference De Concini, Procesi, (Zampieri and D’Agnolo10] or [Reference Brown and Goodearl4, III.6.5]. The finite-dimensional Hopf quotient
$\textrm{dim}T = \textrm{dim}_k(\mathfrak{g})$
; see [Reference De Concini, Procesi, (Zampieri and D’Agnolo10] or [Reference Brown and Goodearl4, III.6.5]. The finite-dimensional Hopf quotient
![]() $\overline{H}=U_\epsilon(\mathfrak{g})/A^+U_\epsilon(\mathfrak{g})$
of
$\overline{H}=U_\epsilon(\mathfrak{g})/A^+U_\epsilon(\mathfrak{g})$
of
![]() $U_\epsilon(\mathfrak{g})$
is the restricted quantized enveloping algebra, denoted by
$U_\epsilon(\mathfrak{g})$
is the restricted quantized enveloping algebra, denoted by
![]() $u_\epsilon(\mathfrak{g})$
.
$u_\epsilon(\mathfrak{g})$
.
Since A is central in
![]() $U_\epsilon(\mathfrak{g})$
$U_\epsilon(\mathfrak{g})$
![]() $(\mathbf{{OrbSemi}})$
holds, but we do not know whether
$(\mathbf{{OrbSemi}})$
holds, but we do not know whether
![]() $(\mathbf{{CoSplit}})$
is valid. However, for the two easiest cases—that is when
$(\mathbf{{CoSplit}})$
is valid. However, for the two easiest cases—that is when
![]() $\mathfrak{g}$
is
$\mathfrak{g}$
is
![]() $\mathfrak{sl}_2$
or
$\mathfrak{sl}_2$
or
![]() $\mathfrak{sl}_3$
-
$\mathfrak{sl}_3$
-
![]() $(\mathbf{{CoSplit}})$
has been confirmed by hand, as follows.
$(\mathbf{{CoSplit}})$
has been confirmed by hand, as follows.
For
![]() $U_\epsilon(\mathfrak{sl}_2)$
with its standard generators
$U_\epsilon(\mathfrak{sl}_2)$
with its standard generators
![]() $\{E,F, K^{\pm 1}\}$
,
$\{E,F, K^{\pm 1}\}$
,
![]() $A = k[E^{\ell}, F^{\ell}, K^{\pm \ell}]$
and one may check that the A-submodule X of
$A = k[E^{\ell}, F^{\ell}, K^{\pm \ell}]$
and one may check that the A-submodule X of
![]() $U_\epsilon(\mathfrak{sl}_2(k))$
generated by
$U_\epsilon(\mathfrak{sl}_2(k))$
generated by
is a coideal of
![]() $U_\epsilon(\mathfrak{sl}_2(k))$
. When
$U_\epsilon(\mathfrak{sl}_2(k))$
. When
![]() $\mathfrak{g}$
is
$\mathfrak{g}$
is
![]() $\mathfrak{sl}_2$
, the group T is a semidirect product,
$\mathfrak{sl}_2$
, the group T is a semidirect product,
![]() $T = (k,+)^2\rtimes k^{\times}$
; see e.g. [Reference Brown and Goodearl4, Section III.6.5]. Let
$T = (k,+)^2\rtimes k^{\times}$
; see e.g. [Reference Brown and Goodearl4, Section III.6.5]. Let
![]() $\mathfrak{t}$
denote its Lie algebra. Since
$\mathfrak{t}$
denote its Lie algebra. Since
![]() $u_\epsilon(\mathfrak{sl}_2)^{\ast} = o_\epsilon(SL(2))$
by [Reference Brown and Goodearl4, Theorem III.7.10], we deduce from Theorem 6.1 that
$u_\epsilon(\mathfrak{sl}_2)^{\ast} = o_\epsilon(SL(2))$
by [Reference Brown and Goodearl4, Theorem III.7.10], we deduce from Theorem 6.1 that
with Hopf subalgebras
![]() $o_\epsilon(SL_2)$
,
$o_\epsilon(SL_2)$
,
![]() $W(U_\epsilon(\mathfrak{sl}_2)^{\circ})\, \;:\!=\; \, o_\epsilon(SL_2)\#U(\mathfrak{t})$
and
$W(U_\epsilon(\mathfrak{sl}_2)^{\circ})\, \;:\!=\; \, o_\epsilon(SL_2)\#U(\mathfrak{t})$
and
![]() $\widehat{kT} \, \;:\!=\; \, o_\epsilon(SL_2)\#kT$
.
$\widehat{kT} \, \;:\!=\; \, o_\epsilon(SL_2)\#kT$
.
For
![]() $ U_\epsilon(\mathfrak{sl}_3)$
, the Hopf centre A is
$ U_\epsilon(\mathfrak{sl}_3)$
, the Hopf centre A is
![]() $\mathcal{O}(S)$
for a Poisson algebraic group S which, using [Reference Brown and Goodearl4, III.6.5], is a semidirect product
$\mathcal{O}(S)$
for a Poisson algebraic group S which, using [Reference Brown and Goodearl4, III.6.5], is a semidirect product
![]() $(k,+)^6 \rtimes (k^{\times})^2$
, whose Lie algebra
$(k,+)^6 \rtimes (k^{\times})^2$
, whose Lie algebra
![]() $\mathfrak{s}$
has basis
$\mathfrak{s}$
has basis
![]() $\lbrace e_1,e_2,e_3,f_1,f_2,f_3,k_1,k_2 \rbrace,$
with non-zero brackets
$\lbrace e_1,e_2,e_3,f_1,f_2,f_3,k_1,k_2 \rbrace,$
with non-zero brackets
An explicit coalgebra A-module complement to A in
![]() $U_\epsilon(\mathfrak{sl}_3)$
has been described as a result of extensive calculations in [Reference Couto11, p. 131 and Appendix A.1], so that
$U_\epsilon(\mathfrak{sl}_3)$
has been described as a result of extensive calculations in [Reference Couto11, p. 131 and Appendix A.1], so that
![]() $A \subseteq U_\epsilon(\mathfrak{sl}_3)$
satisfies
$A \subseteq U_\epsilon(\mathfrak{sl}_3)$
satisfies
![]() $(\mathbf{{CoSplit}})$
. Therefore, applying Theorem 6.1, we obtain
$(\mathbf{{CoSplit}})$
. Therefore, applying Theorem 6.1, we obtain
with Hopf subalgebras
![]() $o_\epsilon(SL_3)$
,
$o_\epsilon(SL_3)$
,
and
In view of these two cases, it seems reasonable to ask.
Question 7.1. Does
![]() $U_\epsilon(\mathfrak{g})$
satisfy
$U_\epsilon(\mathfrak{g})$
satisfy
![]() $(\mathbf{{CoSplit}})$
for all semisimple Lie algebras
$(\mathbf{{CoSplit}})$
for all semisimple Lie algebras
![]() $\mathfrak{g}$
?
$\mathfrak{g}$
?
7.5 Prime regular affine Hopf algebras of Gelfand–Kirillov dimension 1
Here, “regular” means “having finite global dimension,” necessarily then equal to 1. These Hopf k-algebras were classified when k is an algebraically closed field of characteristic 0 by Wu et al. in [Reference Ding12], building on [Reference Brown and Zhang5] and [Reference Lu, Wu and Zhang24]; see also the survey article [Reference Brown and Zhang6]. By a fundamental result of Small et al. [Reference Small, Stafford and Warfield34], a semiprime affine algebra of GK-dimension one is a finite module over its centre. But in fact more is true for these Hopf algebras—they are all commutative-by-finite. This can be checked on a case-by-case basis, as we now briefly outline. For k algebraically closed of characteristic 0, there are two finite families and three infinite families, as follows.
-
(I) The commutative algebras k[x] and
 $k[x^{\pm 1}]$
.
$k[x^{\pm 1}]$
. -
(II) The unique noncommutative cocommutative example, the group algebra
 $H = kD$
of the infinite dihedral group D, defined and discussed in Remarks 3.3(1).
$H = kD$
of the infinite dihedral group D, defined and discussed in Remarks 3.3(1). -
(III) The infinite dimensional Taft algebras
where \begin{equation*}T(n,t,q)\; :\!=\;\; k\langle g,x\;:\;g^n=1, xg=qgx \rangle,\end{equation*}
\begin{equation*}T(n,t,q)\; :\!=\;\; k\langle g,x\;:\;g^n=1, xg=qgx \rangle,\end{equation*}
 $n \in \mathbb{Z}_{\geq 2},$
$n \in \mathbb{Z}_{\geq 2},$
 $1 \leq t \leq n$
and q is a primitive nth root of 1 in k, with g group-like and
$1 \leq t \leq n$
and q is a primitive nth root of 1 in k, with g group-like and
 $\Delta (x) = x \otimes1 + g^t \otimes x$
. With
$\Delta (x) = x \otimes1 + g^t \otimes x$
. With
 $n^{\prime} \;:\!=\;n/\gcd(n,t)$
,
$n^{\prime} \;:\!=\;n/\gcd(n,t)$
,
 $A \;:\!=\;k[x^{n^{\prime}}]$
is a commutative normal Hopf subalgebra.
$A \;:\!=\;k[x^{n^{\prime}}]$
is a commutative normal Hopf subalgebra.
-
(IV) The generalised Liu algebras B(n,w,q), where n and w are positive integers and q is a primitive nth root of 1. Here,
with x and g group-like and \begin{equation*} B(n,w,q) \; :\!=\;\; k\langle x^{\pm 1}, g^{\pm 1}, y\,:\, x \textit{ central},\, yg=qgy, \, g^n=x^w=1-y^n \rangle, \end{equation*}
\begin{equation*} B(n,w,q) \; :\!=\;\; k\langle x^{\pm 1}, g^{\pm 1}, y\,:\, x \textit{ central},\, yg=qgy, \, g^n=x^w=1-y^n \rangle, \end{equation*}
 $\Delta(y) = y \otimes 1 + g\otimes y$
. One can show that
$\Delta(y) = y \otimes 1 + g\otimes y$
. One can show that
 $A\;:\!=\;k[x^{\pm 1}]$
is a central Hopf subalgebra over which B(n,w,q) is free of rank
$A\;:\!=\;k[x^{\pm 1}]$
is a central Hopf subalgebra over which B(n,w,q) is free of rank
 $n^2$
.
$n^2$
.
-
(V) Let m and d be positive integers with
 $(1+m)d$
even, and let q be a primitive
$(1+m)d$
even, and let q be a primitive
 $2m^{\textrm{th}}$
root of 1 in k. The Hopf algebras D(m,d,q) are defined in [Reference Ding12, Section 4.1]. D(m,d,q) is finitely generated over the normal commutative Hopf subalgebra
$2m^{\textrm{th}}$
root of 1 in k. The Hopf algebras D(m,d,q) are defined in [Reference Ding12, Section 4.1]. D(m,d,q) is finitely generated over the normal commutative Hopf subalgebra
 $A\;:\!=\;k[x^{\pm 1}]$
, [Reference Ding12, (4.7)].
$A\;:\!=\;k[x^{\pm 1}]$
, [Reference Ding12, (4.7)].
The above algebras are all free over the listed normal commutative Hopf subalgebras. Families (I)–(IV) are pointed and decompose as crossed products
but D(m,d,q) is not pointed, [Reference Ding12, Proposition 4.9]. Applying Theorems 3.2, 4.3, and 5.13 to these families yields the following information about their Hopf duals, (omitting the algebras in (I) and (II), which are already covered by Sections 3.1 and 7.2). In the proposition, for coprime integers s and m with
![]() $1 \leq s < m$
and a primitive
$1 \leq s < m$
and a primitive
![]() $m^{\textrm{th}}$
root of unity
$m^{\textrm{th}}$
root of unity
![]() $q \in k$
,
$q \in k$
,
![]() $T_f(m,s,q)$
denotes the finite dimensional Taft algebra in these parameters; that is,
$T_f(m,s,q)$
denotes the finite dimensional Taft algebra in these parameters; that is,
![]() $T_f(m,s,q) \;:\!=\; T(m,s,q)/\langle x^m \rangle$
. For a positive integer m,
$T_f(m,s,q) \;:\!=\; T(m,s,q)/\langle x^m \rangle$
. For a positive integer m,
![]() $C_m$
denotes the cyclic group of order m.
$C_m$
denotes the cyclic group of order m.
For reasons of space, we omit some details in the proofs for (III) and (IV), and omit the entire proof of (V). Full proofs can be found in [Reference Couto11] and [Reference Jahn19]; detailed references are listed in Remarks 7.1.
Proposition 7.2. Let k be an algebraically closed field of characteristic 0, and let H be an affine prime regular Hopf k-algebra of Gelfand–Kirillov dimension one, as listed in cases (III), (IV) and (V) above. Then
![]() $(\mathbf{{CoSplit}}$
and
$(\mathbf{{CoSplit}}$
and
![]() $\mathbf{{OrbSemi}})$
hold in all cases, and the finite dual of H takes the following forms.
$\mathbf{{OrbSemi}})$
hold in all cases, and the finite dual of H takes the following forms.
-
(III) Let
 $d\;:\!=\;\textrm{gcd}(n,t),\, n^{\prime}\;:\!=\;n/d,\, t^{\prime}\;:\!=\;t/d$
. Then, as algebras, with Hopf subalgebras
$d\;:\!=\;\textrm{gcd}(n,t),\, n^{\prime}\;:\!=\;n/d,\, t^{\prime}\;:\!=\;t/d$
. Then, as algebras, with Hopf subalgebras \begin{equation*}T(n,t,q)^\circ \; \cong \; kC_d \otimes T_f(n^{\prime},t^{\prime},q^d)\otimes k[f]\otimes k(k,+), \end{equation*}
\begin{equation*}T(n,t,q)^\circ \; \cong \; kC_d \otimes T_f(n^{\prime},t^{\prime},q^d)\otimes k[f]\otimes k(k,+), \end{equation*}
 $kC_d$
,
$kC_d$
,
 $\overline{H}^{\ast} = kC_d \otimes T_f(n^{\prime},t^{\prime},q^d)$
, and
$\overline{H}^{\ast} = kC_d \otimes T_f(n^{\prime},t^{\prime},q^d)$
, and \begin{equation*} W(H^{\circ}) \; = \; kC_d \otimes T_f(n^{\prime},t^{\prime},q^d)\otimes k[f]\end{equation*}
\begin{equation*} W(H^{\circ}) \; = \; kC_d \otimes T_f(n^{\prime},t^{\prime},q^d)\otimes k[f]\end{equation*}
 \begin{equation*} \widehat{kG_H} \; = \; kC_d \otimes T_f(n^{\prime},t^{\prime},q^d)\otimes k(k,+).\end{equation*}
\begin{equation*} \widehat{kG_H} \; = \; kC_d \otimes T_f(n^{\prime},t^{\prime},q^d)\otimes k(k,+).\end{equation*}
-
(IV) When
 $H = B(n,w,q)$
, with Hopf subalgebras
$H = B(n,w,q)$
, with Hopf subalgebras \begin{equation*}H^\circ \; = \; T_f(n,1,q) \# (k[f]\otimes k(k^\times)),\end{equation*}
\begin{equation*}H^\circ \; = \; T_f(n,1,q) \# (k[f]\otimes k(k^\times)),\end{equation*}
 $\overline{H}^{\ast} =T_f(n,1,q)$
,
$\overline{H}^{\ast} =T_f(n,1,q)$
,
 $W(H^{\circ}) = T_f(n,1,q) \# k[f]$
and
$W(H^{\circ}) = T_f(n,1,q) \# k[f]$
and  \begin{equation*}\widehat{kG_H} \; = \; T_f(n,1,q) \# k(k,+).\end{equation*}
\begin{equation*}\widehat{kG_H} \; = \; T_f(n,1,q) \# k(k,+).\end{equation*}
-
(V) When
 $H = D(m,d,q)$
, with Hopf subalgebras
$H = D(m,d,q)$
, with Hopf subalgebras \begin{equation*} H^\circ \; = \; (kC_2\#_\sigma T_f(m,1,q^2)) \# (k[f]\otimes k(k^\times)),\end{equation*}
\begin{equation*} H^\circ \; = \; (kC_2\#_\sigma T_f(m,1,q^2)) \# (k[f]\otimes k(k^\times)),\end{equation*}
 $\overline{H}^{\ast} = kC_2 \#_{\sigma} T_f(m,1,q^2)$
,
$\overline{H}^{\ast} = kC_2 \#_{\sigma} T_f(m,1,q^2)$
,
 $W(H^{\circ}) = \overline{H}^{\ast}\#k[f]$
and
$W(H^{\circ}) = \overline{H}^{\ast}\#k[f]$
and  \begin{equation*} \widehat{kG_H} \; = \; \overline{H}^{\ast} \# k(k^{\times}).\end{equation*}
\begin{equation*} \widehat{kG_H} \; = \; \overline{H}^{\ast} \# k(k^{\times}).\end{equation*}
Proof. (III) Let
![]() $A = k[x^{n^{\prime}}]$
as noted above. Thus
$A = k[x^{n^{\prime}}]$
as noted above. Thus
Thus, as a right A-module
![]() $H = A \oplus X$
, where X is the free right A-module on basis
$H = A \oplus X$
, where X is the free right A-module on basis
![]() $\mathcal{P}$
, where
$\mathcal{P}$
, where
One checks that X is a coideal of H, so that H satisfies
![]() $(\mathbf{{CoSplit}})$
. Moreover, it is clear that, for
$(\mathbf{{CoSplit}})$
. Moreover, it is clear that, for
![]() $ 0\leq i<n,\, 0 \leq j<n^{\prime}$
, the map
$ 0\leq i<n,\, 0 \leq j<n^{\prime}$
, the map
is a cleaving map of coalgebras, so that Theorem 3.2(2) applies, yielding the isomorphism of algebras
It is now straightforward to calculate that, as an algebra,
where
![]() $\tau$
is a cocycle, while as coalgebra
$\tau$
is a cocycle, while as coalgebra
Since
![]() $\textrm{gcd}(n^{\prime},t^{\prime}) = 1$
,
$\textrm{gcd}(n^{\prime},t^{\prime}) = 1$
,
![]() $T_f(n^{\prime},t^{\prime},q^d)$
is self-dual by [Reference Radford28, Exercise 7.4.3], as also is
$T_f(n^{\prime},t^{\prime},q^d)$
is self-dual by [Reference Radford28, Exercise 7.4.3], as also is
![]() $kC_d$
, so we deduce that, as an algebra,
$kC_d$
, so we deduce that, as an algebra,
Combining (7.3), (7.4) and the fact that
![]() $A^{\circ} = k[f] \otimes k(k,+)$
, we deduce the algebra isomorphism in (III), with
$A^{\circ} = k[f] \otimes k(k,+)$
, we deduce the algebra isomorphism in (III), with
![]() $\overline{H}^{\ast}$
a Hopf subalgebra by Lemma 3.1(1). Moreover
$\overline{H}^{\ast}$
a Hopf subalgebra by Lemma 3.1(1). Moreover
![]() $A \subseteq H$
also satisfies
$A \subseteq H$
also satisfies
![]() $(\mathbf{{OrbSemi}})$
since the action of
$(\mathbf{{OrbSemi}})$
since the action of
![]() $\overline{H}$
on A factors through the group algebra
$\overline{H}$
on A factors through the group algebra
![]() $k\langle\overline{g}\rangle$
. Thus the claims regarding
$k\langle\overline{g}\rangle$
. Thus the claims regarding
![]() $W(H^{\circ})$
and
$W(H^{\circ})$
and
![]() $\widehat{kG_H}$
follow, respectively, from Theorems 4.3(5) and 5.13(2)
$\widehat{kG_H}$
follow, respectively, from Theorems 4.3(5) and 5.13(2)
(IV) Let
![]() $H = B(n,w,q)$
, so
$H = B(n,w,q)$
, so
![]() $H = \bigoplus_{0 \leq i,j < n}y^ig^jA$
is a free A-module, and
$H = \bigoplus_{0 \leq i,j < n}y^ig^jA$
is a free A-module, and
As a complement X to A in H choose the A-module generated by
One checks routinely that X is a coideal of H. Therefore
![]() $(\mathbf{{CoSplit}})$
holds, and Theorem 3.2(1) implies that
$(\mathbf{{CoSplit}})$
holds, and Theorem 3.2(1) implies that
by (7.5) and the fact that
![]() $T_f(n,1,q)$
is self-dual by [Reference Radford28, Exercise 7.3.4].
$T_f(n,1,q)$
is self-dual by [Reference Radford28, Exercise 7.3.4].
Since A is central
![]() $A \subseteq H$
satisfies
$A \subseteq H$
satisfies
![]() $(\mathbf{{OrbSemi}})$
, so Theorem 6.1(2) confirms the claims regarding
$(\mathbf{{OrbSemi}})$
, so Theorem 6.1(2) confirms the claims regarding
![]() $W(H^{\circ})$
and
$W(H^{\circ})$
and
![]() $\widehat{kG_H}$
.
$\widehat{kG_H}$
.
(V) The fact that D(m,d,q) satisfies
![]() $(\mathbf{{CoSplit}})$
and
$(\mathbf{{CoSplit}})$
and
![]() $(\mathbf{{OrbSemi}})$
is proved in [Reference Couto11, Section 2.2.5, pp. 52--55 and Proposition 3.1.13], and the structure of its Hopf dual is described in [Reference Couto11, Corollary 4.4.6(V) and Appendix A.2].
$(\mathbf{{OrbSemi}})$
is proved in [Reference Couto11, Section 2.2.5, pp. 52--55 and Proposition 3.1.13], and the structure of its Hopf dual is described in [Reference Couto11, Corollary 4.4.6(V) and Appendix A.2].
Remark 7.1.
-
(1) Precise formulae for the comultiplication for the duals of the Taft algebras (III) have been obtained—for full details see [Reference Couto11, Corollary 4.4.6 and Appendix A.2].
-
(2) In (IV), the smash products in both
 $W(H^{\circ})$
and
$W(H^{\circ})$
and
 $\widehat{k(k^{\times})}$
are non-trivial, hence so is the smash product in
$\widehat{k(k^{\times})}$
are non-trivial, hence so is the smash product in
 $H^{\circ}$
itself. Precise formulae are given in [Reference Couto11, Corollary 4.4.6(4) and Appendix A.2]. Formulae for the coproduct are given at the same reference—in particular, neither k[f] nor
$H^{\circ}$
itself. Precise formulae are given in [Reference Couto11, Corollary 4.4.6(4) and Appendix A.2]. Formulae for the coproduct are given at the same reference—in particular, neither k[f] nor
 $k(k^{\times})$
is a Hopf subalgebra of
$k(k^{\times})$
is a Hopf subalgebra of
 $H^{\circ}$
.
$H^{\circ}$
. -
(3) For completeness, we note some gaps in the above analysis. For the duals of the Taft algebras (III), we only have precise formulae for the coproduct when
 $\textrm{gcd}(n,t) = 1$
; see [Reference Jahn19, Remark 6.12] for this case. For the duals
$\textrm{gcd}(n,t) = 1$
; see [Reference Jahn19, Remark 6.12] for this case. For the duals
 $D(m,d,q)^{\circ}$
in (V), we do not have formulae for the actions of k[f] and
$D(m,d,q)^{\circ}$
in (V), we do not have formulae for the actions of k[f] and
 $k(k^{\times})$
on
$k(k^{\times})$
on
 $\overline{H}^{\ast}$
, nor do we know whether the cocycle
$\overline{H}^{\ast}$
, nor do we know whether the cocycle
 $\sigma$
is non-trivial.
$\sigma$
is non-trivial.
7.6 Noetherian PI Hopf domains of Gelfand-Kirillov dimension two
Let k be algebraically closed of characteristic 0 and let H be a noetherian Hopf k-algebra domain with
![]() ${\textrm{GK dim}} (H) = 2$
. Such Hopf algebras were classified in [Reference Goodearl and Zhang17] under the additional assumption that H has an infinite dimensional commutative factor, or equivalently by [Reference Goodearl and Zhang17, Proposition 3.8(c)] that
${\textrm{GK dim}} (H) = 2$
. Such Hopf algebras were classified in [Reference Goodearl and Zhang17] under the additional assumption that H has an infinite dimensional commutative factor, or equivalently by [Reference Goodearl and Zhang17, Proposition 3.8(c)] that
![]() $ {\textrm{Ext}}_H^1({_Hk},{_Hk})\neq 0.$
$ {\textrm{Ext}}_H^1({_Hk},{_Hk})\neq 0.$
The algebras in this classification which satisfy a polynomial identity (PI) are all easily seen to be commutative-by-finite, as we now indicate. Omitting the 2 group algebras and the rank 2 polynomial algebra, since these have already been discussed, the remaining PI families are as follows, using the numbering scheme of [Reference Goodearl and Zhang17]:
-
(III) Hopf algebras
 $A(\ell, n,q)$
, where
$A(\ell, n,q)$
, where
 $\ell$
and n are integers with
$\ell$
and n are integers with
 $\ell >1$
and
$\ell >1$
and
 $n > 0$
, and q is a primitive
$n > 0$
, and q is a primitive
 $\ell^{\textrm{th}}$
root of 1 in k. As an algebra the localised quantum plane, with x group-like and
$\ell^{\textrm{th}}$
root of 1 in k. As an algebra the localised quantum plane, with x group-like and \begin{equation*} A(\ell, n , q) \; :\!=\; k\langle x^{\pm 1},y\;:\;xy = qyx \rangle, \end{equation*}
\begin{equation*} A(\ell, n , q) \; :\!=\; k\langle x^{\pm 1},y\;:\;xy = qyx \rangle, \end{equation*}
 $\Delta (y) = y \otimes 1 + x^n \otimes y$
. These algebras are free of finite rank over the normal commutative Hopf subalgebra
$\Delta (y) = y \otimes 1 + x^n \otimes y$
. These algebras are free of finite rank over the normal commutative Hopf subalgebra
 $A\;:\!=\;k [x^{\pm \ell}, y^{\ell'} ]$
, where
$A\;:\!=\;k [x^{\pm \ell}, y^{\ell'} ]$
, where
 $\ell' \;:\!=\; \ell/ \gcd (n, \ell)$
.
$\ell' \;:\!=\; \ell/ \gcd (n, \ell)$
.
-
(IV) Hopf algebras
 $B(n, p_0, \dots , p_s,q)$
, where
$B(n, p_0, \dots , p_s,q)$
, where
 $s \geq 2$
,
$s \geq 2$
,
 $n,p_0,\ldots , p_s$
are positive integers with
$n,p_0,\ldots , p_s$
are positive integers with
 $p_0 \mid n$
and
$p_0 \mid n$
and
 $\{p_i \;:\;i \geq 1 \}$
strictly increasing and pairwise relatively prime, and q is a primitive
$\{p_i \;:\;i \geq 1 \}$
strictly increasing and pairwise relatively prime, and q is a primitive
 $\ell^{\textrm{th}}$
root of 1 where
$\ell^{\textrm{th}}$
root of 1 where
 $\ell \;:\!=\; (n/p_0)p_1 \ldots p_s$
. Then
$\ell \;:\!=\; (n/p_0)p_1 \ldots p_s$
. Then
 $B(n, p_0, \dots , p_s,q)$
is the subalgebra of the localised quantum plane from (III) generated by
$B(n, p_0, \dots , p_s,q)$
is the subalgebra of the localised quantum plane from (III) generated by
 $\{x^{\pm 1}, y^{m_i} \;:\;1 \leq i \leq s \}$
, where
$\{x^{\pm 1}, y^{m_i} \;:\;1 \leq i \leq s \}$
, where
 $m_i \;:\!=\; \Pi_{j \neq i} p_j.$
This is a Hopf subalgebra of
$m_i \;:\!=\; \Pi_{j \neq i} p_j.$
This is a Hopf subalgebra of
 $A(\ell,n,q)$
, with x group-like and
$A(\ell,n,q)$
, with x group-like and
 $\Delta(y^{m_i}) = y\otimes 1 + x^{m_i n} \otimes y$
. One can easily check that
$\Delta(y^{m_i}) = y\otimes 1 + x^{m_i n} \otimes y$
. One can easily check that
 $A \;:\!=\; k[ y^{p_1 \cdots p_s}, x^{\pm \ell} ]$
is a normal commutative Hopf subalgebra over which
$A \;:\!=\; k[ y^{p_1 \cdots p_s}, x^{\pm \ell} ]$
is a normal commutative Hopf subalgebra over which
 $B(n,p_0,\ldots , p_s,q)$
is a finite module.
$B(n,p_0,\ldots , p_s,q)$
is a finite module.
We proceed to describe the Hopf duals of these algebras. Once again we leave some calculations to the reader in order to save space; details of the omitted arguments can be found in [Reference Jahn19] or [Reference Couto11].
Proposition 7.3. Let k be an algebraically closed field of characteristic 0, and let H be a noetherian Hopf k-algebra domain of GK-dimension 2 with
![]() $\textrm{Ext}_H(k,k) \neq 0$
, as listed above. Then H satisfies
$\textrm{Ext}_H(k,k) \neq 0$
, as listed above. Then H satisfies
![]() $(\mathbf{{CoSplit}})$
and
$(\mathbf{{CoSplit}})$
and
![]() $(\mathbf{{OrbSemi}})$
, and so the Hopf dual
$(\mathbf{{OrbSemi}})$
, and so the Hopf dual
![]() $H^{\circ}$
of H has the following form.
$H^{\circ}$
of H has the following form.
-
(III) When
 $H = A(\ell,n,q)$
, let
$H = A(\ell,n,q)$
, let
 $d\;:\!=\;\textrm{gcd}(n,\ell), \, \ell'\;:\!=\;\ell/d, \, n^{\prime}\;:\!=\;n/d.$
Then with Hopf subalgebras
$d\;:\!=\;\textrm{gcd}(n,\ell), \, \ell'\;:\!=\;\ell/d, \, n^{\prime}\;:\!=\;n/d.$
Then with Hopf subalgebras \begin{equation*} H^{\circ} \; \cong \; (kC_d \otimes T_f(\ell',n^{\prime},q^{-d})) \# (k[f,f']\otimes k((k,+)\times k^\times)),\end{equation*}
\begin{equation*} H^{\circ} \; \cong \; (kC_d \otimes T_f(\ell',n^{\prime},q^{-d})) \# (k[f,f']\otimes k((k,+)\times k^\times)),\end{equation*}
 $\overline{H} \cong kC_d \otimes T_f(\ell',n^{\prime},q^{-d})$
, and
$\overline{H} \cong kC_d \otimes T_f(\ell',n^{\prime},q^{-d})$
, and \begin{equation*} W(H^{\circ}) \; \cong \; (kC_d \otimes T_f(\ell',n^{\prime},q^{-d})) \# k[f,f']\end{equation*}
\begin{equation*} W(H^{\circ}) \; \cong \; (kC_d \otimes T_f(\ell',n^{\prime},q^{-d})) \# k[f,f']\end{equation*}
 \begin{equation*} \widehat{kG_H} \; \cong \; (kC_d \otimes T_f(\ell',n^{\prime},q^{-d})) \# k((k,+)\times k^{\times}).\end{equation*}
\begin{equation*} \widehat{kG_H} \; \cong \; (kC_d \otimes T_f(\ell',n^{\prime},q^{-d})) \# k((k,+)\times k^{\times}).\end{equation*}
-
(IV) When
 $H = B(n, p_0, \dots , p_s,q)$
, define
$H = B(n, p_0, \dots , p_s,q)$
, define
 $\xi_i \;:\!=\; q^{-(n/p_0)m_i}$
, for
$\xi_i \;:\!=\; q^{-(n/p_0)m_i}$
, for
 $i = 1, \ldots , s$
, so
$i = 1, \ldots , s$
, so
 $\xi$
is a primitive
$\xi$
is a primitive
 $p_i^{\textrm{th}}$
root of unity. Then with Hopf subalgebras
$p_i^{\textrm{th}}$
root of unity. Then with Hopf subalgebras \begin{equation*} H^{\circ} \; \cong \; (kC_{n/p_0}\otimes T_f(p_1,p_0p_2\ldots p_s, \xi_1) \otimes \ldots \otimes T_f(p_s,p_0,\xi_s)) \#(k[f,f']\otimes k((k,+)\times k^\times)),\end{equation*}
\begin{equation*} H^{\circ} \; \cong \; (kC_{n/p_0}\otimes T_f(p_1,p_0p_2\ldots p_s, \xi_1) \otimes \ldots \otimes T_f(p_s,p_0,\xi_s)) \#(k[f,f']\otimes k((k,+)\times k^\times)),\end{equation*}
 \begin{equation*}\overline{H}^{\ast} \; \cong \; kC_{n/p_0}\otimes T_f(p_1,p_0p_2\ldots p_s, \xi_1) \otimes \ldots \otimes T_f(p_s,p_0,\xi_s),\end{equation*}
and
\begin{equation*}\overline{H}^{\ast} \; \cong \; kC_{n/p_0}\otimes T_f(p_1,p_0p_2\ldots p_s, \xi_1) \otimes \ldots \otimes T_f(p_s,p_0,\xi_s),\end{equation*}
and \begin{equation*} W(H^{\circ}) \; \cong \; (kC_{n/p_0}\otimes T_f(p_1,p_0p_2\ldots p_s, \xi_1) \otimes \ldots \otimes T_f(p_s,p_0,\xi_s)) \# k[f,f']\end{equation*}
\begin{equation*} W(H^{\circ}) \; \cong \; (kC_{n/p_0}\otimes T_f(p_1,p_0p_2\ldots p_s, \xi_1) \otimes \ldots \otimes T_f(p_s,p_0,\xi_s)) \# k[f,f']\end{equation*}
 \begin{equation*} \widehat{kG_H} \; \cong \; (kC_{n/p_0}\otimes T_f(p_1,p_0p_2\ldots p_s, \xi_1) \otimes \ldots \otimes T_f(p_s,p_0,\xi_s)) \# k((k,+)\times k^\times). \end{equation*}
\begin{equation*} \widehat{kG_H} \; \cong \; (kC_{n/p_0}\otimes T_f(p_1,p_0p_2\ldots p_s, \xi_1) \otimes \ldots \otimes T_f(p_s,p_0,\xi_s)) \# k((k,+)\times k^\times). \end{equation*}
Proof. (III) As noted above,
![]() $A\;:\!=\;k [x^{\pm \ell}, y^{\ell'} ]$
is a normal commutative Hopf subalgebra of H. It is clear that H is a free right A-module on the basis
$A\;:\!=\;k [x^{\pm \ell}, y^{\ell'} ]$
is a normal commutative Hopf subalgebra of H. It is clear that H is a free right A-module on the basis
![]() $\{y^i x^j \;:\;0 \leq i \leq \ell', \, 0 \leq j < \ell \}$
. By a straightforward analysis detailed in [Reference Couto11, Example 1.1.21 and Section 2.2.6], as algebras
$\{y^i x^j \;:\;0 \leq i \leq \ell', \, 0 \leq j < \ell \}$
. By a straightforward analysis detailed in [Reference Couto11, Example 1.1.21 and Section 2.2.6], as algebras
for a cocycle
![]() $\sigma$
which is in general non-trivial; and, as coalgebras,
$\sigma$
which is in general non-trivial; and, as coalgebras,
Since
![]() $\textrm{gcd}(n^{\prime},\ell') = 1$
, both tensorands in (7.6) are self-dual (using [Reference Radford28, Exercise 7.3.4] for the left-hand one), and hence
$\textrm{gcd}(n^{\prime},\ell') = 1$
, both tensorands in (7.6) are self-dual (using [Reference Radford28, Exercise 7.3.4] for the left-hand one), and hence
as algebras. Moreover
![]() $A \cong \mathcal{O}((k,+)\times k^{\times})$
, so that, as Hopf algebras,
$A \cong \mathcal{O}((k,+)\times k^{\times})$
, so that, as Hopf algebras,
as recalled in Section 3.1.
Let X be the right A-submodule of H generated by
![]() $ \lbrace y^ix^j \;:\;1\leq i<\ell', 0\leq j<\ell \rbrace \cup \lbrace x^j-1\;:\;1\leq j<\ell \rbrace$
. Clearly
$ \lbrace y^ix^j \;:\;1\leq i<\ell', 0\leq j<\ell \rbrace \cup \lbrace x^j-1\;:\;1\leq j<\ell \rbrace$
. Clearly
![]() $H = A \oplus X$
, and it is routine to check that X is a coideal of H. Therefore,
$H = A \oplus X$
, and it is routine to check that X is a coideal of H. Therefore,
![]() $A \subseteq H$
satisfies
$A \subseteq H$
satisfies
![]() $(\mathbf{{CoSplit}})$
.
$(\mathbf{{CoSplit}})$
.
Thus Theorem 3.2(1) applies, and with (7.7) and (7.8) it yields the isomorphism of algebras
with Hopf subalgebra
![]() $ (kC_d \otimes T_f(\ell', n^{\prime}, q^{-d}))$
.
$ (kC_d \otimes T_f(\ell', n^{\prime}, q^{-d}))$
.
It is routine to check that the adjoint action of
![]() $\overline{H}$
on A factors through the group algebra
$\overline{H}$
on A factors through the group algebra
![]() $kC_{\ell} = k\langle \overline{x} \rangle$
, so that
$kC_{\ell} = k\langle \overline{x} \rangle$
, so that
![]() $A \subseteq H$
satisfies
$A \subseteq H$
satisfies
![]() $(\mathbf{{OrbSemi}})$
. Therefore, Theorem 6.1(2) yields the remaining parts of (III).
$(\mathbf{{OrbSemi}})$
. Therefore, Theorem 6.1(2) yields the remaining parts of (III).
(IV) With
![]() $A = k[y^{p_1 \cdots p_s}, x^{\pm \ell}]$
, a commutative normal Hopf subalgebra of H, one can check that H is a free right A-module on the basis
$A = k[y^{p_1 \cdots p_s}, x^{\pm \ell}]$
, a commutative normal Hopf subalgebra of H, one can check that H is a free right A-module on the basis
![]() $\{ y_1^{i_1}\ldots y_s^{i_s}x^j \;:\;0\leq j<\ell, 0\leq i_t < p_t \} $
. The structure of the quotient Hopf algebra
$\{ y_1^{i_1}\ldots y_s^{i_s}x^j \;:\;0\leq j<\ell, 0\leq i_t < p_t \} $
. The structure of the quotient Hopf algebra
![]() $\overline{H} \;:\!=\; H/A^+ H$
has been analysed in [Reference Couto11, Lemma 2.2.5]. As an algebra it is an iterated crossed product whose detailed description we do not need here; but as a coalgebra it decomposes as
$\overline{H} \;:\!=\; H/A^+ H$
has been analysed in [Reference Couto11, Lemma 2.2.5]. As an algebra it is an iterated crossed product whose detailed description we do not need here; but as a coalgebra it decomposes as
Since the above tensorands are all self-dual because the
![]() $p_i$
are mutually coprime [Reference Radford28, Exercise 7.4.3], we deduce that, as an algebra,
$p_i$
are mutually coprime [Reference Radford28, Exercise 7.4.3], we deduce that, as an algebra,
Just as in (III),
Define X to be the right A-module generated by
Then X is a free A-module on the basis
![]() $\mathcal{B}$
with
$\mathcal{B}$
with
![]() $H = A \oplus X$
. It is routine to confirm that X is a coideal of H, so that
$H = A \oplus X$
. It is routine to confirm that X is a coideal of H, so that
![]() $A \subseteq H$
satisfies
$A \subseteq H$
satisfies
![]() $(\mathbf{{CoSplit}})$
. Therefore, Theorem 3.2(1) applies implying that
$(\mathbf{{CoSplit}})$
. Therefore, Theorem 3.2(1) applies implying that
Combining (7.9), (7.10) and (7.11) gives the first two isomorphisms in (IV).
Finally, note that the adjoint action of each of the elements
![]() $y_i$
on A is trivial. Therefore, the action of
$y_i$
on A is trivial. Therefore, the action of
![]() $\overline{H}$
on A factors through the group algebra
$\overline{H}$
on A factors through the group algebra
![]() $kC_{\ell} = k\langle \overline{x}\rangle$
. Hence,
$kC_{\ell} = k\langle \overline{x}\rangle$
. Hence,
![]() $A \subseteq H$
satisfies
$A \subseteq H$
satisfies
![]() $(\mathbf{{OrbSemi}})$
, and so the final two isomorphisms in (IV) follow from Theorem 6.1(2).
$(\mathbf{{OrbSemi}})$
, and so the final two isomorphisms in (IV) follow from Theorem 6.1(2).
Remark 7.2. For the algebras in Proposition 7.3, further information on the definition of the generators of
![]() $H^{\circ}$
is obtained in [Reference Couto11, Corollary 4.4.8 and Appendix A.3].
$H^{\circ}$
is obtained in [Reference Couto11, Corollary 4.4.8 and Appendix A.3].