Published online by Cambridge University Press: 01 December 2021
We prove that a finite index regular inclusion of 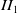 $II_1$
-factors with commutative first relative commutant is always a crossed product subfactor with respect to a minimal action of a biconnected weak Kac algebra. Prior to this, we prove that every finite index inclusion of
$II_1$
-factors with commutative first relative commutant is always a crossed product subfactor with respect to a minimal action of a biconnected weak Kac algebra. Prior to this, we prove that every finite index inclusion of 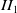 $II_1$
-factors which is of depth 2 and has simple first relative commutant (respectively, is regular and has commutative or simple first relative commutant) admits a two-sided Pimsner–Popa basis (respectively, a unitary orthonormal basis).
$II_1$
-factors which is of depth 2 and has simple first relative commutant (respectively, is regular and has commutative or simple first relative commutant) admits a two-sided Pimsner–Popa basis (respectively, a unitary orthonormal basis).
In memory of Vaughan Jones, a true pioneer!