Article contents
Extension of partial endomorphisms of abelian groups
Published online by Cambridge University Press: 18 May 2009
Extract
It is known [1] that for a partial endomorphism μ of a group G that maps the subgroup A ⊆ G onto B ⊆ G. G to be extendable to a total endomorphism μ* of a supergroup G* ⊆ G such that μ an isomorphism on G*(μ*)m for some positive integer m, it is necessary and sufficient that there exist in G a sequence of normal subgroups
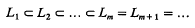
such that L1 ƞA is the kernel of μ and

for ι = 1, 2,…, m–1.
The question then arises whether these conditions could be simplified when the group G is abelian. In this paper it is shown not only that the conditions are simplified when Gis abelian but also that the extension group G*⊇G can be chosen as an abelian group.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1963
References
REFERENCE
- 2
- Cited by


