Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-12T02:55:26.231Z Has data issue: false hasContentIssue false
  • English
  • Français

Extended Schauder decompositions of locally convex spaces†

Published online by Cambridge University Press:  18 May 2009

J. H. Webb
J. H. Webb
Affiliation:
University of Cape Town, Rondebosch, C.P., South Africa
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let E[τ] be a locally convex Hausdorff topological vector space. An extended decomposition of E[τ] is a family {Ea}α∈A of closed subspaces of E such that, for each x in E and each α in A, there exists a unique point xα in Eα, with 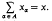Here convergence will have the following meaning. Let Ф denote the set of all finite subsets of A. The sum 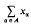is said to be convergent to x if for each neighbourhood U of 0 in E, there is an element φ0 of Ф such that 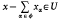, for all φ in Ф containing φ0. It follows that 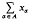is Cauchy if and only if, for each neighbourhood U of 0 in E, there is an element φ0 of Ф such that 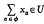, for all φ in Ф disjoint from φ0.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 15 , Issue 2 , September 1974 , pp. 166 - 171
Copyright
Copyright © Glasgow Mathematical Journal Trust 1974

References

REFERENCES

1.Amemiya, I. and Kōmura, Y., Über nicht-vollständige Montelräume, Math. Ann. 177 (1968), 273–277.CrossRefGoogle Scholar
2.Arsove, M. G. and Edwards, R. E., Generalized bases in topological linear spaces, Studia Math. 19 (1960), 95–113.CrossRefGoogle Scholar
3.Bennett, G. and Cooper, J. B., Weak bases in (F)- and (LF)-spaces, J. London Math. Soc. 44 (1969), 505–508.CrossRefGoogle Scholar
4.de Wilde, M. and Houet, C., On increasing sequences of absolutely convex sets in locally convex spaces, Math. Ann. 192 (1971), 257–261.CrossRefGoogle Scholar
5.Dieudonné, J. and Schwartz, L., La dualité dans les espaces (F) et (LF), Ann. Inst. Fourier 1 (1950), 61–101.CrossRefGoogle Scholar
6.Garling, D. J. H. and Kalton, N. J., Colloquium on nuclear spaces and ideals in operator algebras, Studio Math. 38 (1970), 474.Google Scholar
7.Kalton, N. J., Schauder decompositions and completeness, Bull. London Math. Soc. 2 (1970), 34–36.CrossRefGoogle Scholar
8.Knowles, R. J. and Cook, T. A., Non-complete reflexive spaces without Schauder bases, Proc. Cambridge Philos. Soc. 74 (1973), 83–86.CrossRefGoogle Scholar
9.McArthur, C. W., Developments in Schauder basis theory, Bull. Amer. Math. Soc. 78 (1972), 877–908.CrossRefGoogle Scholar
10.Marti, J. T., A weak basis theorem for non-separable Fréchet spaces, J. London Math. Soc. (2) 5 (1972), 8–10.CrossRefGoogle Scholar
11.Tweddle, I., Unconditional convergence and bases, Proc. Edinburgh Math. Soc.; to appear.Google Scholar
12.Webb, J. H., Schauder bases and decompositions in locally convex spaces, Proc. Cambridge Philos Soc. 76 (1974), 145–152.CrossRefGoogle Scholar