Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T07:35:12.086Z Has data issue: false hasContentIssue false
  • English
  • Français

EXISTENCE RESULT FOR NONUNIFORMLY DEGENERATE SEMILINEAR ELLIPTIC SYSTEMS IN 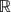N

Published online by Cambridge University Press:  01 September 2009

NGUYEN THANH CHUNG  and
HOANG QUOC TOAN
NGUYEN THANH CHUNG
Affiliation:
Department of Mathematics and Informatics, Quang Binh University, 312 Ly Thuong Kiet, Dong Hoi, Vietnam e-mail: [email protected]
HOANG QUOC TOAN
Affiliation:
Department of Mathematics, Hanoi University of Science, 334 Nguyen Trai, Hanoi, Vietnam e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the existence of solutions for a class of nonuniformly degenerate elliptic systems in 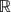N, N ≥ 3, of the form 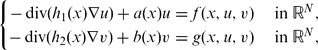where hi ∈ L1loc(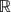N), hi(x) ≧ γ0|x|α with α ∈ (0, 2) and γ0 > 0, i = 1, 2. The proofs rely essentially on a variant of the Mountain pass theorem (D. M. Duc, Nonlinear singular elliptic equations, J. Lond. Math. Soc. 40(2) (1989), 420–440) combined with the Caffarelli–Kohn–Nirenberg inequality (First order interpolation inequalities with weights, Composito Math. 53 (1984), 259–275).

Keywords

35J6535J20
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 3 , September 2009 , pp. 561 - 570
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Ambrosetti, A. and Rabinowitz, P. H., Dual variational methods in critical points theory and applications, J. Funct. Anal. 4 (1973), 349–381.Google Scholar
2.Brezis, H., Analyse fonctionelle théorie et applications Masson, 1992.Google Scholar
3.Caffarelli, L., Kohn, R. and Nirenberg, L., First order interpolation inequalities with weights, Composito Math. 53 (1984), 259–275.Google Scholar
4.Caldiroli, P. and Musina, R., On the existence of extremal functions for a weighted Sobolev embedding with critical exponent, Calc. Var. Partial Differential Equations 8 (4) (1999), 365–387.CrossRefGoogle Scholar
5.Catrina, F. and Wang, Z. Q., On the Caffarelli-Kohn-Nirenberg inequalities: sharp constants, existence (and nonexistence) and symmetry of extremal functions, Comm. Pure Appl. Math. 54 (2001), 229–258.Google Scholar
6.Chung, N. T., Existence of weak solutions for a nonuniformly elliptic nonlinear system in N, EJDE 119 (2008), 1–10.Google Scholar
7.Costa, D. G., On a class of elliptic systems in N, EJDE 07 (1994), 1–14.Google Scholar
8.Duc, D. M., Nonlinear singular elliptic equations, J. Lond. Math. Soc. 40 (2) (1989), 420–440.CrossRefGoogle Scholar
9.Gazzola, F. and Radulescu, V., A nonsmooth critical point theory approach to some nonlinear elliptic equations in N, Differential Integr. Equations 13 (1–3) 2000, 47–60.CrossRefGoogle Scholar
10.Mihăilescu, M., Nonlinear eigenvalue problems for some degenerate elliptic operators on N, Bull. Belg. Math. Soc. 12 (2005), 435–448.Google Scholar
11.Mihăilescu, M., Existence and multiplicity of weak solutions for a class of denegerate nonlinear elliptic equations, Boundary Value Probl. (2006), Art. ID 41295, 17 pp.Google Scholar
12.Mihăilescu, M. and Rădulescu, V., Ground state solutions of nonlinear singular Schrödinger equations with lack of compactness, Math. Methods Appl. Sci. 26 (2003), 897–906.CrossRefGoogle Scholar
13.Motreanu, D. and Rădulescu, V., Eigenvalue problems for degenerate nonlinear elliptic equations in anisotropic media, Boundary Value Probl. 2 (2005), 107–127.Google Scholar
14.Radulescu, V. and Smets, D., Critical singular problems on infinite cones, Nonlinear Anal. 54 (6) (2003), 1153–1164.Google Scholar