Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T12:51:34.174Z Has data issue: false hasContentIssue false
  • English
  • Français

EXISTENCE OF MONOTONIC ASYMPTOTICALLY CONSTANT SOLUTIONS FOR SECOND ORDER DIFFERENTIAL EQUATIONS

Published online by Cambridge University Press:  01 September 2007

CRISTÓBAL GONZÁLEZ  and
ANTONIO JIMÉNEZ-MELADO
CRISTÓBAL GONZÁLEZ
Affiliation:
Dept. Análisis Matemático, Fac. Ciencias, Univ. Málaga, 29071 Málaga, Spain e-mails: [email protected], [email protected]
ANTONIO JIMÉNEZ-MELADO
Affiliation:
Dept. Análisis Matemático, Fac. Ciencias, Univ. Málaga, 29071 Málaga, Spain e-mails: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Starting from results of Dubé and Mingarelli, Wahlén, and Ehrström, who give conditions that ensure the existence and uniqueness of nonnegative nondecreasing solutions asymptotically constant of the equation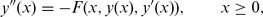 we have been able to reduce their hypotheses in order to obtain the same existence results, at the expense of losing the uniqueness part. The main tool they used is the Banach Fixed Point Theorem, while ours has been the Schauder Fixed Point Theorem together with one version of the Arzelà-Ascoli Theorem.

Keywords

34A1234A3434C10
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 49 , Issue 3 , September 2007 , pp. 515 - 523
Copyright
Copyright © Glasgow Mathematical Journal Trust 2007

References

REFERENCES

1.Constantin, A., On the existence of positive solutions of second order differential equations, Ann. Mat. Pura Appl. (4) 184 (2005), no. 2, 131–138.CrossRefGoogle Scholar
2.Dubé, S. D. and Mingarelli, A. B., Note on a non-oscillation theorem of Atkinson, Electron. J. Differential Equations 2004 (2004), no. 22 1–6, available at http://ejde.math.txstate.edu.Google Scholar
3.Ehrnström, M., Positive solutions for second-order nonlinear differential equations Nonlinear Anal. 64 (2006), 1608–1620.CrossRefGoogle Scholar
4.Lipovan, O., On the asymptotic behaviour of the solutions to a class of second order nonlinear differential equations, Glasgow Math. J. 45 (2003), 179–187.CrossRefGoogle Scholar
5.Mustafa, O. G. and Rogovchenko, Y. V., Global existence of solutions with prescribed asymptotic behavior for second-order nonlinear differential equations, Nonlinear Anal. 51 (2002), 339–368.CrossRefGoogle Scholar
6.Wahlén, E., Positive solutions of second-order differential equations, Nonlinear Anal. 58 (2004), 359–366.CrossRefGoogle Scholar
7.Yin, Z., Monotone positive solutions of second-order nonlinear differential equations, Nonlinear Anal. 54 (2003), 391–403.CrossRefGoogle Scholar