Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-20T17:38:56.240Z Has data issue: false hasContentIssue false
  • English
  • Français

EXCEPTIONAL ZEROES OF P-ADIC L-FUNCTIONS OVER NON-ABELIAN FIELD EXTENSIONS

Part of: Discontinuous groups and automorphic forms Arithmetic algebraic geometry

Published online by Cambridge University Press:  21 July 2015

DANIEL DELBOURGO
DANIEL DELBOURGO*
Affiliation:
Department of Mathematics, University of Waikato, Hamilton 3240, New Zealand e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose E is an elliptic curve over 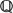$\Bbb Q$, and p>3 is a split multiplicative prime for E. Let q ≠ p be an auxiliary prime, and fix an integer m coprime to pq. We prove the generalised Mazur–Tate–Teitelbaum conjecture for E at the prime p, over number fields 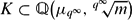$K\subset \Bbb Q\big(\mu_{{q^{\infty}}},\;\!^{q^{\infty}\!\!\!\!}\sqrt{m}\big)$ such that p remains inert in 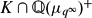$K\cap\Bbb Q(\mu_{{q^{\infty}}})^+$. The proof makes use of an improved p-adic L-function, which can be associated to the Rankin convolution of two Hilbert modular forms of unequal parallel weight.

MSC classification

Primary: 11F33: Congruences for modular and $p$-adic modular forms
Secondary: 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 58 , Issue 2 , May 2016 , pp. 385 - 432
Copyright
Copyright © Glasgow Mathematical Journal Trust 2015 

References

REFERENCES

1.Barré-Sireix, K., Diaz, G., Gramain, F. and Philibert, G., Une preuve de la conjecture Mahler-Manin, Inventiones Math. 124 (1996), 1–9.Google Scholar
2.Dabrowski, A., p-adic L-functions of Hilbert modular forms, Ann. l'Institut Fourier 44 (1994), 1025–1041.CrossRefGoogle Scholar
3.Delbourgo, D., Elliptic curves and big Galois representations, LMS Lecture Notes in Mathematics, vol. 356 (Cambridge University Press, 2008).CrossRefGoogle Scholar
4.Delbourgo, D. and Lei, A., Non-commutative Iwasawa theory for elliptic curves with multiplicative reduction, submitted 2013.Google Scholar
5.Delbourgo, D. and Ward, T., Non-abelian congruences between L-values of elliptic curves, Ann. l'Institut Fourier 58 (3) (2008), 1023–1055.CrossRefGoogle Scholar
6.Deligne, P. and Ribet, K., Values of abelian L-functions at negative integers over totally real fields, Inventiones Math. 59 (1980), 227–286.CrossRefGoogle Scholar
7.Greenberg, R. and Stevens, G., p-adic L-functions and p-adic periods of modular forms, Inventiones Math. 111 (1993), 401–447.Google Scholar
8.Hida, H., On p-adic L-functions of GL(2) × GL(2) over totally real fields, Ann. l'Institut Fourier 41 (1991), 311–391.Google Scholar
9.Hida, H., On p-adic Hecke algebras for GL2 over totally real fields, Ann. Math. 128 (2) (1988), 295–384.CrossRefGoogle Scholar
10.Hida, H., Hilbert modular forms and Iwasawa theory (Oxford University Press, Oxford, 2006).Google Scholar
11.Hida, H., Hecke fields of analytic families of modular forms, J. Am. Math. Soc. 24 (2011), 51–80.CrossRefGoogle Scholar
12.Jones, J., Iwasawa L-functions for multiplicative abelian varieties, Duke Math. J. 59 (1989), 399–420.Google Scholar
13.Mazur, B. and Swinnerton-Dyer, P., Arithmetic of Weil curves, Inventiones Math. 25 (1974), 1–61.CrossRefGoogle Scholar
14.Mazur, B., Tate, J. and Teitelbaum, J., On p–adic analogues of the conjectures of Birch and Swinnerton-Dyer, Inventiones Math. 84 (1986), 1–48.CrossRefGoogle Scholar
15.Mok, C. P., The exceptional zero conjecture for Hilbert modular forms, Compos. Math. 145 (1) (2009), 1–55.Google Scholar
16.Panchiskin, A. A., The convolutions of Hilbert modular forms and their non–Archimedean analogues, Math. USSR Sbornik 64 (2) (1989), 571–584.CrossRefGoogle Scholar
17.Panchiskin, A. A., Non-Archimedean L-functions of Siegel and Hilbert modular forms, Lecture Notes in Mathematics vol. 1471 (Springer-Verlag, 1991).Google Scholar
18.Shimura, G., The special values of the zeta functions associated with Hilbert modular forms, Duke Math. J. 45 (1978), 637–679.Google Scholar
19.Spieß, M., On special zeros of p-adic L-functions of Hilbert modular forms, Inventiones Math. 196 (2014), 69–138.CrossRefGoogle Scholar
20.Tate, J., Number theoretic background, Proc. of Symposia in Pure Mathematics 33 (2) (1979), 3–26.Google Scholar
21.Vishik, M., Nonarchimedean measures connected with Dirichlet series, Math. USSR Sbornik 28 (1976), 216–228.Google Scholar
22.Wiles, A., On the ordinary λ-adic representations associated to Hilbert modular forms, Inventiones Math. 94 (1988), 529–573.CrossRefGoogle Scholar