No CrossRef data available.
Article contents
EVALUATION OF CONVOLUTION SUMS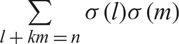 
$$\sum\limits_{l + km = n} {\sigma (l)\sigma (m)} $$ AND 
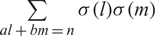$$\sum\limits_{al + bm = n} {\sigma (l)\sigma (m)} $$ FOR k = a · b = 21, 33, AND 35
Part of:
Discontinuous groups and automorphic forms
Elementary number theory
Forms and linear algebraic groups
Zeta and $L$-functions: analytic theory
Published online by Cambridge University Press: 16 July 2021
Abstract
The article focuses on the evaluation of convolution sums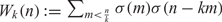 
$${W_k}(n): = \mathop \sum \nolimits_{_{m < {n \over k}}} \sigma (m)\sigma (n - km)$$ involving the sum of divisor function 
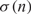$$\sigma (n)$$ for k =21, 33, and 35. In this article, our aim is to obtain certain Eisenstein series of level 21 and use them to evaluate the convolution sums for level 21. We also make use of the existing Eisenstein series identities for level 33 and 35 in evaluating the convolution sums for level 33 and 35. Most of the convolution sums were evaluated using the theory of modular forms, whereas we have devised a technique which is free from the theory of modular forms. As an application, we determine a formula for the number of representations of a positive integer n by the octonary quadratic form 
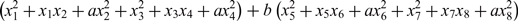$$(x_1^2 + {x_1}{x_2} + ax_2^2 + x_3^2 + {x_3}{x_4} + ax_4^2) + b(x_5^2 + {x_5}{x_6} + ax_6^2 + x_7^2 + {x_7}{x_8} + ax_8^2)$$, for (a, b)=(1, 7), (1, 11), (2, 3), and (2, 5).
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
References
Alaca, A., Alaca, Ş. and Williams, K. S., Evaluation of the convolution sums 
$$\mathop \sum \nolimits_{ _{l + 12m = n}}\sigma (l)\sigma (m)$$ and $$\mathop \sum \nolimits_{ _{3l + 4m = n}}\sigma (l)\sigma (m)$$, Adv. Theor.
Appl. Math. 1(1) (2006), 27–48.Google Scholar
$$\mathop \sum \nolimits_{ _{l + 12m = n}}\sigma (l)\sigma (m)$$ and 
$$\mathop \sum \nolimits_{ _{3l + 4m = n}}\sigma (l)\sigma (m)$$, Adv. Theor.
Appl. Math. 1(1) (2006), 27–48.Google ScholarAlaca, A., Alaca, Ş. and Williams, K. S., Evaluation of the convolution sums $$\mathop \sum \nolimits_{ _{l + 18m = n}}\sigma (l)\sigma (m)$$ and $$\mathop \sum \nolimits_{ _{2l + 9m = n}}\sigma (l)\sigma (m)$$, Int. Math.
Forum 2(1–4) (2007), 45–68.Google Scholar
$$\mathop \sum \nolimits_{ _{l + 18m = n}}\sigma (l)\sigma (m)$$ and 
$$\mathop \sum \nolimits_{ _{2l + 9m = n}}\sigma (l)\sigma (m)$$, Int. Math.
Forum 2(1–4) (2007), 45–68.Google ScholarAlaca, A., Alaca, Ş., and Williams, K. S., Evaluation of the convolution sums $$\mathop \sum \nolimits_{ _{l + 24m = n}}\sigma (l)\sigma (m)$$ and $$\mathop \sum \nolimits_{ _{3l + 8m = n}}\sigma (l)\sigma (m)$$, Math. J. Okayama Univ. 49 (2007), 93–111.Google Scholar
$$\mathop \sum \nolimits_{ _{l + 24m = n}}\sigma (l)\sigma (m)$$ and 
$$\mathop \sum \nolimits_{ _{3l + 8m = n}}\sigma (l)\sigma (m)$$, Math. J. Okayama Univ. 49 (2007), 93–111.Google ScholarAlaca, A., Alaca, Ş. and Williams, K. S., The convolution sum $$\mathop \sum \nolimits_{ _{m < n/16}}\sigma (m)\sigma (n - 16m)$$, Canad. Math. Bull. 51(1) (2008), 3–14.CrossRefGoogle Scholar
$$\mathop \sum \nolimits_{ _{m < n/16}}\sigma (m)\sigma (n - 16m)$$, Canad. Math. Bull. 51(1) (2008), 3–14.CrossRefGoogle ScholarAlaca, Ş. and Kesicioğlu, Y., Evaluation of the convolution sums $$\mathop \sum \nolimits_{ _{l + 27m = n}}\sigma (l)\sigma (m)$$ and $$\mathop \sum \nolimits_{ _{l + 32m = n}}\sigma (l)\sigma (m)$$, Int.
J. Number Theory 12(1) (2016), 1–13.CrossRefGoogle Scholar
$$\mathop \sum \nolimits_{ _{l + 27m = n}}\sigma (l)\sigma (m)$$ and 
$$\mathop \sum \nolimits_{ _{l + 32m = n}}\sigma (l)\sigma (m)$$, Int.
J. Number Theory 12(1) (2016), 1–13.CrossRefGoogle ScholarAlaca, Ş. and Williams, K. S., Evaluation of the convolution sums $$\mathop \sum \nolimits_{ _{l + 6m = n}}\sigma (l)\sigma (m)$$ and $$\mathop \sum \nolimits_{ _{2l + 3m = n}}\sigma (l)\sigma (m)$$, J. Number Theory 124(2) (2007), 491–510.CrossRefGoogle Scholar
$$\mathop \sum \nolimits_{ _{l + 6m = n}}\sigma (l)\sigma (m)$$ and 
$$\mathop \sum \nolimits_{ _{2l + 3m = n}}\sigma (l)\sigma (m)$$, J. Number Theory 124(2) (2007), 491–510.CrossRefGoogle ScholarAndrews, G. E. and Berndt, B. C., Ramanujan’s lost notebook, part I (Springer, New York, 2005).CrossRefGoogle Scholar
Anusha, T., Bhuvan, E. N., Cooper, S. and Vasuki, K. R., Elliptic integrals and Ramanujan-type series for $$1/\pi $$ associated with $${\Gamma _0}(N)$$, where N is a product of two small primes, J. Math. Anal. Appl. 472(2) (2019), 1551–1570.CrossRefGoogle Scholar
$$1/\pi $$ associated with 
$${\Gamma _0}(N)$$, where N is a product of two small primes, J. Math. Anal. Appl. 472(2) (2019), 1551–1570.CrossRefGoogle ScholarBerndt, B. C., Chan, H. H., Sohn, J. and Son, S. H., Eisenstein series in Ramanujan’s lost notebook, Ramanujan J. 4(1) (2000), 81–114.CrossRefGoogle Scholar
Besge, M., Extrait d’une lettre de M Besge á M Liouville, J. Math. Pure Appl. 7 (1862), 256.Google Scholar
Bhuvan, E. N.. A classical approach to Ramanujan’s type Eisenstein series and incomplete elliptic integrals, Doctorial Thesis (submitted to University of Mysore, Mysuru, India, 2018).Google Scholar
Chan, H. H. and Cooper, S., Powers of theta functions, Pacific J. Math. 235(1) (2008), 1–14.CrossRefGoogle Scholar
Cooper, S., Ramanujan’s theta functions (Springer International Publishing, AG, 2017).CrossRefGoogle Scholar
Cooper, S. and Toh, P. C., Quintic and septic Eisenstein series, Ramanujan J. 19(2) (2009), 163–181.CrossRefGoogle Scholar
Cooper, S. and Ye, D., Evaluation of the convolution sums $$\mathop \sum \nolimits_{ _{l + 20m = n}}\sigma (l)\sigma (m)$$, $$\mathop \sum \nolimits_{ _{4l + 5m = n}}\sigma (l)\sigma (m)$$ and $$\mathop \sum \nolimits_{ _{2l + 5m = n}}\sigma (l)\sigma (m)$$, Int.
J. Number Theory 10(6) (2014), 1385–1394.CrossRefGoogle Scholar
$$\mathop \sum \nolimits_{ _{l + 20m = n}}\sigma (l)\sigma (m)$$, 
$$\mathop \sum \nolimits_{ _{4l + 5m = n}}\sigma (l)\sigma (m)$$ and 
$$\mathop \sum \nolimits_{ _{2l + 5m = n}}\sigma (l)\sigma (m)$$, Int.
J. Number Theory 10(6) (2014), 1385–1394.CrossRefGoogle ScholarGlaisher, J. W. L., On the square of the series in which the coefficients are the sums of the divisors of the exponents, Messenger Math. 14 (1862), 156–163.Google Scholar
Glaisher, J. W. L., Mathematical papers (W. Metcalfe and Son, Cambridge, 1885), 1883–1885.Google Scholar
Huard, J. G., Ou, Z. M., Spearman, B. K. and Williams, K. S., Elementary evaluation of certain convolution sums involving divisor functions, in Number theory for the millennium, II (Urbana, IL, 2000) (A K Peters, Natick, MA, 2002), 229–274.Google Scholar
Lemire, M. and Williams, K. S., Evaluation of two convolution sums involving the sum of divisors function, Bull. Austral. Math. Soc. 73(1)(2006), 107–115.CrossRefGoogle Scholar
Lomadze, G. A., Representation of numbers by sums of the quadratic forms $$x_1^2 + {x_1}{x_2} + x_2^2$$, Acta Arith. 54(1) (1989), 9–36.Google Scholar
$$x_1^2 + {x_1}{x_2} + x_2^2$$, Acta Arith. 54(1) (1989), 9–36.Google ScholarNtienjem, E., Evaluation of the convolution sums $$\mathop \sum \nolimits_{ _{\alpha l + \beta m = n}}\sigma (l)\sigma (m)$$ where $$(\alpha ,\beta )$$ is in {(1, 14), (2, 7), (1, 26), (2, 13), (1, 28), (4, 7), (1, 30), (2, 15), (3, 10), (5, 6)}, Master’s Thesis (School of Mathematics and Statistics, Carleton University, 2015).Google Scholar
$$\mathop \sum \nolimits_{ _{\alpha l + \beta m = n}}\sigma (l)\sigma (m)$$ where 
$$(\alpha ,\beta )$$ is in {(1, 14), (2, 7), (1, 26), (2, 13), (1, 28), (4, 7), (1, 30), (2, 15), (3, 10), (5, 6)}, Master’s Thesis (School of Mathematics and Statistics, Carleton University, 2015).Google ScholarNtienjem, E., Evaluation of convolution sums involving the sum of divisors function for levels 48 and 64, Integers 17 Paper No. A49, 22 (2017).Google Scholar
Ntienjem, E., Evaluation of the convolution sum involving the sum of divisors function for 22, 44 and 52, Open Math. 15(1) (2017), 446–458.CrossRefGoogle Scholar
Ntienjem, E., Elementary evaluation of convolution sums involving the divisor function for a class of levels, North-W. Eur. J. Math. 5 (2019), 101–165.Google Scholar
Ramakrishnan, B. and Sahu, B., Evaluation of the convolution sums $$\mathop \sum \nolimits_{ _{l + 15m = n}}\sigma (l)\sigma (m)$$ and $$\mathop \sum \nolimits_{ _{3l + 5m = n}}\sigma (l)\sigma (m)$$ and an application, Int.
J. Number Theory 9(3) (2013), 799–809.CrossRefGoogle Scholar
$$\mathop \sum \nolimits_{ _{l + 15m = n}}\sigma (l)\sigma (m)$$ and 
$$\mathop \sum \nolimits_{ _{3l + 5m = n}}\sigma (l)\sigma (m)$$ and an application, Int.
J. Number Theory 9(3) (2013), 799–809.CrossRefGoogle ScholarRamanujan, S., Notebooks (2 volumes) (Tata Institute of Fundamental Research, Bombay, 1957).Google Scholar
Ramanujan, S., The lost notebook and other unpublished papers (Narosa Publishing House, New Delhi, 1988).Google Scholar
Ramanujan, S., On certain arithmetical functions [Trans. Cambridge Philos. Soc. 22(9) (1916), 159–184], in Collected papers of Srinivasa Ramanujan (AMS Chelsea Publishing, Providence, RI, 2000), 136–162.Google Scholar
Royer, E., Evaluating convolution sums of the divisor function by quasimodular forms, Int. J. Number Theory 3(2) (2007), 231–261.CrossRefGoogle Scholar
Vasuki, K. R. and Veeresha, R. G., Ramanujan’s Eisenstein series of level 7 and 14, J. Number Theory 159 (2016), 59–75.CrossRefGoogle Scholar
Williams, K. S., The convolution sum $$\mathop \sum \nolimits_{ _{m < n/9}}\sigma (m)\sigma (n - 9m)$$, Int.
J. Number Theory 1(2) (2005), 193–205.CrossRefGoogle Scholar
$$\mathop \sum \nolimits_{ _{m < n/9}}\sigma (m)\sigma (n - 9m)$$, Int.
J. Number Theory 1(2) (2005), 193–205.CrossRefGoogle ScholarWilliams, K. S., The convolution sum $$\mathop \sum \nolimits_{ _{m < n/8}}\sigma (m)\sigma (n - 8m)$$, Pacific J. Math. 228(2) (2006), 387–396.CrossRefGoogle Scholar
$$\mathop \sum \nolimits_{ _{m < n/8}}\sigma (m)\sigma (n - 8m)$$, Pacific J. Math. 228(2) (2006), 387–396.CrossRefGoogle ScholarXia, E. X. W., Tian, X. L., and Yao, O. X. M., Evaluation of the convolution sum $$\mathop \sum \nolimits_{ _{i + 25j = n}}\sigma (i)\sigma (j)$$, Int.
J. Number Theory 10(6) (2014), 1421–1430.CrossRefGoogle Scholar
$$\mathop \sum \nolimits_{ _{i + 25j = n}}\sigma (i)\sigma (j)$$, Int.
J. Number Theory 10(6) (2014), 1421–1430.CrossRefGoogle ScholarYe, D., Evaluation of the convolution sums $$\mathop \sum \nolimits_{ _{l + 36m = n}}\sigma (l)\sigma (m)$$ and $$\mathop \sum \nolimits_{ _{4l + 9m = n}}\sigma (l)\sigma (m)$$, Int.
J. Number Theory 11(1) (2015), 171–183.CrossRefGoogle Scholar
$$\mathop \sum \nolimits_{ _{l + 36m = n}}\sigma (l)\sigma (m)$$ and 
$$\mathop \sum \nolimits_{ _{4l + 9m = n}}\sigma (l)\sigma (m)$$, Int.
J. Number Theory 11(1) (2015), 171–183.CrossRefGoogle Scholar