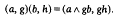Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pastijn, F.
1980.
Semilattices with a transitive automorphism group.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 29,
Issue. 1,
p.
29.
McAlister, D.B.
1980.
Semigroups.
p.
1.
Meakin, John
and
Pastijn, Francis
1981.
The structure of pseudo-semilattices.
Algebra Universalis,
Vol. 13,
Issue. 1,
p.
355.
Pastijn, F.
1981.
Division theorems for inverse and pseudo-inverse semigroups.
Journal of the Australian Mathematical Society,
Vol. 31,
Issue. 4,
p.
415.
Pastijn, Francis
1982.
Inverse semigroup varieties generated by E-unitary inverse semigroups.
Semigroup Forum,
Vol. 24,
Issue. 1,
p.
87.
Petrich, Mario
and
Reilly, Norman R.
1982.
A network of congruences on an inverse semigroup.
Transactions of the American Mathematical Society,
Vol. 270,
Issue. 1,
p.
309.
Lawson, M. V.
1993.
An equivalence theorem for inverse semigroups.
Semigroup Forum,
Vol. 47,
Issue. 1,
p.
7.
Lawson, M. V.
1993.
A note on a paper of Joubert.
Semigroup Forum,
Vol. 47,
Issue. 1,
p.
389.
Lawson, M. V.
1994.
Almost factorisable inverse semigroups.
Glasgow Mathematical Journal,
Vol. 36,
Issue. 1,
p.
97.
Lawson, M. V.
1996.
Enlargements of regular semigroups.
Proceedings of the Edinburgh Mathematical Society,
Vol. 39,
Issue. 3,
p.
425.
Giraldes, E.
Marques-Smith, P.
and
Mitsch, H.
2004.
F-regular semigroups.
Journal of Algebra,
Vol. 274,
Issue. 2,
p.
491.
Billhardt, Bernd
2006.
Regular Semigroups Each of Whose Least Completely Simple Congruence Classes Has a Greatest Element.
Communications in Algebra,
Vol. 34,
Issue. 10,
p.
3629.
Guo, Xiaojiang
Ni, Xiangfei
and
Shum, K. P.
2008.
GENERALIZATION OF F-INVERSE SEMIGROUPS BY USING MCALISTER'S APPROACH.
Asian-European Journal of Mathematics,
Vol. 01,
Issue. 04,
p.
535.
Tabatabaie Shourijeh, Bahman
Jokar, Asghar
and
Buchholz, Detlev
2011.
Tight Representations of 0‐E‐Unitary Inverse Semigroups.
Abstract and Applied Analysis,
Vol. 2011,
Issue. 1,
Guo, Xiaojiang
and
Shum, K. P.
2011.
Proper LeftGC-lppSemigroups and a Generalized Version of McAlister's P-Theorem.
Algebra Colloquium,
Vol. 18,
Issue. 03,
p.
475.
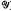 ) consisting of a down-directed partially ordered set ℋ, an ideal and subsemilattice
) consisting of a down-directed partially ordered set ℋ, an ideal and subsemilattice 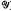 of ℋ and a group G acting on ℋ, on the left, by order automorphisms in such a way that ℋ = G
of ℋ and a group G acting on ℋ, on the left, by order automorphisms in such a way that ℋ = G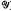 . This semigroup is denoted by P(G, ℋ,
. This semigroup is denoted by P(G, ℋ, 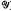 ); it consists of all pairs (a, g)∈
); it consists of all pairs (a, g)∈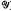 × G such that g−1a ∈
× G such that g−1a ∈ 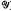 , under the multiplication
, under the multiplication