Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-23T09:32:43.772Z Has data issue: false hasContentIssue false
  • English
  • Français

E-unitary congruences on inverse semigroups

Published online by Cambridge University Press:  18 May 2009

N. R. Reilly  and
W. D. Munn
N. R. Reilly
Affiliation:
Simon Fraser University, Burnaby 2, B.C., Canada
W. D. Munn
Affiliation:
University of Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By an E-unitary inverse semigroup we mean an inverse semigroup in which the semilattice is a unitary subset. Such semigroups, elsewhere called ‘proper’ or ‘reduced’ inverse semigroups, have been the object of much recent study. Free inverse semigroups form a subclass of particular interest.

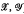An important structure theorem for E-unitary inverse semigroups has been obtained by McAlister [4, 5]. From a triple (G, ) consisting of a group G, a partially ordered set 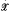and a subset 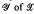, satisfying certain conditions, he constructs an E-unitary inverse semigroup P(G, 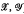). A semigroup of this type is called a P-semigroup. The structure theorem states that every E-unitary inverse semigroup is, to within isomorphism, of this form. A second theorem asserts that every inverse semigroup is isomorphic to a quotient of a Psemigroup by an idempotent-separating congruence. We refer below to these results as McAlister's Theorems A and B respectively. A triple (C, 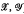) of the type used to construct a P-semigroup is here termed a “McAlister triple”. It is shown further, in [5], that there is essentially only one such triple corresponding to a given E-unitary inverse semigroup.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 17 , Issue 1 , January 1976 , pp. 57 - 75
Copyright
Copyright © Glasgow Mathematical Journal Trust 1976

References

REFERENCES

1.Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Math. Surveys of the Amer. Math. Soc. 7 (Providence, R.I., 1961 (vol. 1) and 1967 (vol. 2))Google Scholar
2.Green, D. G., Extensions of a semilattice by an inverse semigroup, Bull. Austral. Math. Soc. 9 (1973), 21–31CrossRefGoogle Scholar
3.Howie, J. M., The maximum idempotent-separating congruence on an inverse semigroup, Proc. Edinburgh Math. Soc. (2) 14 (1964), 71–79CrossRefGoogle Scholar
4.McAlister, D. B., Groups, semilattices and inverse semigroups, Trans. Amer. Math. Soc. 192 (1974), 227–244Google Scholar
5.McAlister, D. B., Groups, semilattices and inverse semigroups II, Trans. Amer. Math. Soc. 196 (1974), 351–370CrossRefGoogle Scholar
6.McAlister, D. B. and McFadden, R., Zig-zag representations and inverse semigroups, J. Algebra 32 (1974), 178–206CrossRefGoogle Scholar
7.McFadden, R. and O'Carroll, L., F-inverse semigroups, Proc. London Math. Soc. (3) 22 (1971), 652–666Google Scholar
8.Munn, W. D., A class of irreducible matrix representations of an arbitrary inverse semigroup, Proc. Glasgow Math. Assoc. 5 (1961), 41–48Google Scholar
9.Munn, W. D., Fundamental inverse semigroups, Quarterly J. Math. Oxford (2) 21 (1970), 157–170CrossRefGoogle Scholar
10.Munn, W. D., Free inverse semigroups, Semigroup Forum 5 (1973), 262–269. (Research announcement.)CrossRefGoogle Scholar
11.Munn, W. D., Free inverse semigroups, Proc. London Math. Soc. (3) 29 (1974), 385–404CrossRefGoogle Scholar
12.O'Carroll, L., Reduced inverse semigroups, Semigroup Forum 8 (1974), 270–276. (Research announcement.)CrossRefGoogle Scholar
13.O'Carroll, L., Reduced inverse and partially ordered semigroups, J. London Math. Soc. (2) 9 (1974), 293–301CrossRefGoogle Scholar
14.Preston, G. B., Free inverse semigroups, J. Austral. Math. Soc. 16 (1973), 443–453Google Scholar
15.Reilly, N. R., Free generators of free inverse semigroups, Bull. Austral. Math. Soc. 7 (1972), 407–424CrossRefGoogle Scholar
16.Reilly, N. R., E-unitary inverse semigroups, Math. Dept. Research Report, Simon Fraser University (1975)Google Scholar
17.Reilly, N. R. and Scheiblich, H. E., Congruences on regular semigroups, Pacific J. Math. 23 (1967), 349–360Google Scholar
18.Scheiblich, H. E., Free inverse semigroups, Semigroup Forum 4 (1972), 351–359. (Research announcement.)CrossRefGoogle Scholar
19.Scheiblich, H. E., Free inverse semigroups, Proc. Amer. Math. Soc. 38 (1973), 1–7CrossRefGoogle Scholar
20.Saitô, T., Proper ordered inverse semigroups, Pacific J. Math. 15 (1965), 649–666Google Scholar