Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T08:12:23.439Z Has data issue: false hasContentIssue false
  • English
  • Français

EQUIVARIANT ANDERSON DUALITY AND MACKEY FUNCTOR DUALITY

Part of: Topological $K$-theory Homology and cohomology theories

Published online by Cambridge University Press:  21 July 2015

NICOLAS RICKA
NICOLAS RICKA*
Affiliation:
Laboratoire Analyse, Géométrie et Applications, UMR 7539, 99, avenue Jean-Baptiste Clément, 93430 Villetaneuse, France e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the 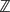$\mathbb{Z}$/2-equivariant nth integral Morava K-theory with reality is self-dual with respect to equivariant Anderson duality. In particular, there is a universal coefficients exact sequence in integral Morava K-theory with reality, and we recover the self-duality of the spectrum KO as a corollary. The study of 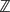$\mathbb{Z}$/2-equivariant Anderson duality made in this paper gives a nice interpretation of some symmetries of RO(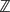$\mathbb{Z}$/2)-graded (i.e. bigraded) equivariant cohomology groups in terms of Mackey functor duality.

MSC classification

Primary: 55N91: Equivariant homology and cohomology
Secondary: 19L47: Equivariant $K$-theory
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 58 , Issue 3 , September 2016 , pp. 649 - 676
Copyright
Copyright © Glasgow Mathematical Journal Trust 2015 

References

REFERENCES

1. Anderson, D. W., Universal coefficient theorems for k-theory (University California, Berkeley, CA, 1969).Google Scholar
2. Atiyah, M. F., K-theory and reality, Quart. J. Math. Oxford Ser. (2) 17 (1966), 367–386.Google Scholar
3. Brown, E. H. Jr and Comenetz, M., Pontrjagin duality for generalized homology and cohomology theories, Amer. J. Math. 98 (1) (1976), 1–27.Google Scholar
4. Ferland, K. K. and Gaunce Lewis, L. Jr, The RO(G)-graded equivariant ordinary homology of G-cell complexes with even-dimensional cells for G = $\mathbb{Z}$ /p , Mem. Amer. Math. Soc. 167 (794) (2004), viii+129.Google Scholar
5. Hill, M. A., Hopkins, M. J. and Ravenel, D. C., On the non-existence of elements of Kervaire invariant one, ArXiv e-prints, May 2015.Google Scholar
6. Hu, P. and Kriz, I., Real-oriented homotopy theory and an analogue of the Adams-Novikov spectral sequence, Topology 40 (2) (2001), 317–399.Google Scholar
7. Heard, D. and Stojanoska, V., K-theory, reality, and duality, ArXiv e-prints, May 2014.CrossRefGoogle Scholar
8. Kainen, P. C., Universal coefficient theorems for generalized homology and stable cohomotopy, Pacific J. Math. 37 (1971), 397–407.Google Scholar
9. Gaunce Lewis, L. Jr, Change of universe functors in equivariant stable homotopy theory, Fund. Math. 148 (2) (1995), 117–158.Google Scholar
10. Lewis, L. G. Jr, May, J. P., Steinberger, M. and McClure, J. E., Equivariant stable homotopy theory, Lecture Notes in Mathematics, vol. 1213 (Springer-Verlag, Berlin, 1986), With contributions by J. E. McClure.Google Scholar
11. May, J. P., Equivariant homotopy and cohomology theory, CBMS Regional Conference Series in Mathematics, vol. 91, Published for the Conference Board of the Mathematical Sciences, Washington, DC, 1996 (American Mathematical Society, Providence, RI), With contributions by Cole, M., Comezaña, G., Costenoble, S., Elmendorf, A. D., Greenlees, J. P. C., Lewis, L. G. Jr, Piacenza, R. J., Triantafillou, G. and Waner, S..CrossRefGoogle Scholar
12. Mandell, M. A. and May, J. P., Equivariant orthogonal spectra and S-modules, Mem. Amer. Math. Soc. 159 (755) (2002), x+108.Google Scholar
13. Stojanoska, V., Duality for topological modular forms, ArXiv e-prints, May 2011.CrossRefGoogle Scholar
14. Thévenaz, J. and Webb, P., The structure of Mackey functors, Trans. Amer. Math. Soc. 347 (6) (1995), 1865–1961.Google Scholar