Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T08:15:37.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Embedding inverse semigroups of homeomorphisms on closed subsets

Published online by Cambridge University Press:  18 May 2009

Bridget Bos Baird
Bridget Bos Baird
Affiliation:
State University of New York at Buffalo, Amherst, New York 14226, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

All topological spaces here are assumed to be T2. The collection 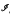F(Y)of all homeomorphisms whose domains and ranges are closed subsets of a topological space Y is an inverse semigroup under the operation of composition. We are interested in the general problem of getting some information about the subsemigroups of 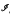F(Y) whenever Y is a compact metric space. Here, we specifically look at the problem of determining those spaces X with the property that 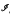F(X) is isomorphic to a subsemigroup of 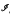F(Y). The main result states that if X is any first countable space with an uncountable number of points, then the semigroup 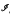F(X) can be embedded into the semigroup 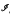F(Y) if and only if either X is compact and Y contains a copy of X, or X is noncompact and locally compact and Y contains a copy of the one-point compactification of X.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 18 , Issue 2 , July 1977 , pp. 199 - 207
Copyright
Copyright © Glasgow Mathematical Journal Trust 1977

References

REFERENCES

1.Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Math. Surveys of the Amer. Math. Soc. 7 Vol 1 (Providence, R.I., 1961) and Vol. 2 (Providence, R.I., 1967).Google Scholar
2.Dugundji, J., Topology (Allyn and Bacon, Inc., 1967).Google Scholar
3.Kuratowski, K., Topology Vol. 1 (Academic Press, 1966).Google Scholar
4.Preston, G. B., Representations of inverse semi-groups, J. London Math. Soc. 29 (1954), 411–419.CrossRefGoogle Scholar
5.Vagner, V. V., Generalized Groups, Dokl. Akad. Nauk SSSR (N.S.) 84 (1952), 1119–1122.Google Scholar