Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T08:16:55.491Z Has data issue: false hasContentIssue false
  • English
  • Français

EIGENVALUES OF GEOMETRIC OPERATORS RELATED TO THE WITTEN LAPLACIAN UNDER THE RICCI FLOW

Part of: Global differential geometry

Published online by Cambridge University Press:  27 February 2017

SHOUWEN FANG ,
FEI YANG  and
PENG ZHU
SHOUWEN FANG
Affiliation:
School of Mathematical Science, Yangzhou University, Yangzhou, Jiangsu 225002, P. R. China e-mail: [email protected]
FEI YANG
Affiliation:
School of Mathematics and physics, China University of Geosciences, Wuhan 430074, P. R. China e-mail: [email protected]
PENG ZHU
Affiliation:
School of Mathematics and physics, Jiangsu University of Technology, Changzhou, Jiangsu 213001, P. R. China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (M, g(t)) be a compact Riemannian manifold and the metric g(t) evolve by the Ricci flow. In the paper, we prove that the eigenvalues of geometric operator −Δφ + 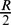$\frac{R}{2}$ are non-decreasing under the Ricci flow for manifold M with some curvature conditions, where Δφ is the Witten Laplacian operator, φ ∈ C2(M), and R is the scalar curvature with respect to the metric g(t). We also derive the evolution of eigenvalues under the normalized Ricci flow. As a consequence, we show that compact steady Ricci breather with these curvature conditions must be trivial.

MSC classification

Primary: 53C21: Methods of Riemannian geometry, including PDE methods; curvature restrictions
Secondary: 53C44: Geometric evolution equations (mean curvature flow, Ricci flow, etc.)
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 59 , Issue 3 , September 2017 , pp. 743 - 751
Copyright
Copyright © Glasgow Mathematical Journal Trust 2017 

References

REFERENCES

1. Cao, H. D. and Zhu, X. P., A complete proof of the Poincaré and Geometrization conjectures—Application of the Hamilton-Perelman theory of the Ricci flow, Asian J. Math. 10 (2006), 165–492.CrossRefGoogle Scholar
2. Cao, X. D., Eigenvalues of (−Δ + $\frac{R}{2}$ ) on manifolds with nonnegative curvature operator, Math. Ann. 337 (2007), 435–441.CrossRefGoogle Scholar
3. Cao, X. D., First eigenvalues geometric operators under the Ricci flow, Proc. Amer. Math. Soc. 136 (2008), 4075–4078.CrossRefGoogle Scholar
4. Fang, S. W., Xu, H. F. and Zhu, P., Evolution and monotonicity of eigenvalues under the Ricci flow, Sci. China Math. 58 (2015), 1737–1744.CrossRefGoogle Scholar
5. Guo, H. X., Philipowski, R. and Thalmaier, A., Entropy and lowest eigenvalue on evolving manifolds, Pacific J. Math. 264 (2013), 61–82.CrossRefGoogle Scholar
6. Hamilton, R., Three-manifolds with positive Ricci curvature, J. Diff. Geom. 17 (1982), 255–306.Google Scholar
7. Hamilton, R., Four-manifolds with positive curvature operator, J. Diff. Geom. 24 (1986), 153–179.Google Scholar
8. Ivey, T., Ricci solitons on compact three-manifolds, Differ. Geom. Appl. 3 (1993), 301–307.CrossRefGoogle Scholar
9. Li, J. F., Eigenvalues and energy functionals with monotonicity formulae under Ricci flow, Math. Ann. 338 (2007), 927–946.CrossRefGoogle Scholar
10. Li, X. D., Liouville theorems for symmetric diffusion operators on complete Riemannian manifolds, J. Math. Pures Appl. 84 (2005), 1295–1361.CrossRefGoogle Scholar
11. Ling, J., A comparison theorem and a sharp bound via the Ricci flow, http://arxiv.org/abs/0710.2574.Google Scholar
12. Ling, J., A class of monotonic quantities along the Ricci flow, http://arxiv.org/abs/0710.4291.Google Scholar
13. Ma, L., Eigenvalue monotonicity for the Ricci-Hamilton flow, Ann. Global Anal. Geom. 29 (2006), 287–292.CrossRefGoogle Scholar
14. Perelman, G., The entropy formula for the Ricci flow and its geometric applications, http://arxiv.org/abs/math/0211159.Google Scholar
15. Xia, C. Y. and Xu, H. W., Inequalities for eigenvalues of the drifting Laplacian on Riemannian manifolds, Ann. Global Anal. Geom. 45 (2014), 155–166.CrossRefGoogle Scholar
16. Zhao, L., The first eigenvalue of the Laplace operator under Yamabe flow, Mathematica Applicata 24 (2011), 274–278.Google Scholar