1. Introduction
Derived categories play an important role in many branches of mathematics such as algebraic geometry and representation theory, where they provide the proper setting for tilting theory [Reference Bongartz9, Reference Brenner and Butler10, Reference Happel and Ringel25].
In general, giving a concrete description of the (bounded) derived category of a finite dimensional algebra is not easy to achieve. However, when the derived category is tame, this is often possible, and a geometric realisation or a combinatorial description of their indecomposables objects and morphisms has been given for several families of well-known algebras, such as hereditary algebras of Dynkin type or gentle algebras [Reference Bekkert and Merklen6, Reference Haiden, Katzarkov and Kontsevich23, Reference Happel24, Reference Lekili and Polishchuk32, Reference Opper, Plamondon and Schroll35].
The derived categories of gentle algebras have been gaining relevance in several branches of mathematics; for example, recently these categories have been linked to homological mirror symmetry, a homological framework developed by Kontsevich [Reference Kontsevich29] to explain the similarities between the symplectic geometry of the so-called A-model, and the algebraic geometry of the so-called B-model of certain Calabi-Yau manifolds. Derived categories of gentle algebras have provided a good understanding of the A-model in the mirror symmetry program in the case of surfaces. In particular, a connection between graded gentle algebras and Fukaya categories was established in [Reference Bocklandt8, Reference Haiden, Katzarkov and Kontsevich23], where collections of formal generators in (partially wrapped) Fukaya categories were constructed whose endomorphism algebras are graded gentle algebras. Conversely, in [Reference Lekili and Polishchuk32, Reference Opper, Plamondon and Schroll35], given a homologically smooth graded gentle algebra A, a graded surface with stops
![]() $(S_A, M_A, \eta_A)$
is constructed, where
$(S_A, M_A, \eta_A)$
is constructed, where
![]() $S_A$
is an oriented smooth surface with non-empty boundary,
$S_A$
is an oriented smooth surface with non-empty boundary,
![]() $M_A$
is a set of stops on the boundary of A and
$M_A$
is a set of stops on the boundary of A and
![]() $\eta_A$
is a line field on A, such that the partially wrapped Fukaya category
$\eta_A$
is a line field on A, such that the partially wrapped Fukaya category
![]() $\mathcal W(S_A, M_A, \eta_A)$
and derived category
$\mathcal W(S_A, M_A, \eta_A)$
and derived category
![]() $\mathcal D(A)$
are equivalent.
$\mathcal D(A)$
are equivalent.
Skew-gentle algebras, skew group algebras of gentle algebras, have recently been related to other areas of mathematics where they have been a tool to prove some interesting results. For instance, in [Reference Geiß, Labardini-Fragoso and Schröer17], triangulations giving rise to skew-gentle Jacobian algebras are used to establish the tameness of the Jacobian algebras associated with triangulations of surfaces, see [Reference Labardini-Fragoso30, Reference Labardini-Fragoso31]. These triangulations in [Reference Geiß, Labardini-Fragoso and Schröer17] were used in [Reference Qiu and Zhou36] to study the cluster category of punctured surfaces with non-empty boundary where it is shown that there is a bijection between so-called strings in a skew-gentle algebra and tagged curves in the corresponding surface. In [Reference Amiot and Plamondon2], a geometric construction of these cluster categories via a
![]() $\mathbb{Z}/2$
actions on surfaces is given. In [Reference Valdivieso-Díaz41], skew-gentle algebras were used to prove that Jacobian algebras coming from triangulations of closed surfaces are algebras of exponential growth, an unexpected result uncovering a new class of symmetric tame
$\mathbb{Z}/2$
actions on surfaces is given. In [Reference Valdivieso-Díaz41], skew-gentle algebras were used to prove that Jacobian algebras coming from triangulations of closed surfaces are algebras of exponential growth, an unexpected result uncovering a new class of symmetric tame
![]() $\Omega$
-periodic algebras. Furthermore, in [Reference He, Zhou and Zhu26], a geometric model for the module category of a skew-gentle algebra has been given in terms of tagged dissections of surfaces.
$\Omega$
-periodic algebras. Furthermore, in [Reference He, Zhou and Zhu26], a geometric model for the module category of a skew-gentle algebra has been given in terms of tagged dissections of surfaces.
The bounded derived categories of skew-gentle algebras have been studied by several authors beginning with [Reference Bekkert, Marcos and Merklen5]. In that paper, the authors give a classification of the indecomposable objects in terms of so-called generalised homotopy strings and bands. In [Reference Burban and Drozd11], another classification of the indecomposable objects is given by using different matrix reduction techniques. In [Reference Amiot and Brüstle1], a geometric classification of the derived equivalence classes of skew-gentle algebras is given based on the
![]() $\mathbb{Z}/2$
-action using the geometric model and results for gentle algebras in [Reference Amiot, Plamondon and Schroll3, Reference Opper, Plamondon and Schroll35].
$\mathbb{Z}/2$
-action using the geometric model and results for gentle algebras in [Reference Amiot, Plamondon and Schroll3, Reference Opper, Plamondon and Schroll35].
In the present paper, we realise the indecomposable objects of the bounded derived category of a skew-gentle algebra as curves on a surface with orbifold points of order two. Furthermore, using non-commutative Gröbner bases theory, we give a direct proof that skew-gentle algebras are strong Koszul, a property that is not known to be preserved under skew group action. We show that the Koszul dual is skew-gentle and that its geometric model has the same underlying surface.
More specifically, we show that there is a bijection between skew-gentle algebras and generalised dissections of surfaces with orbifold points of order two or simply orbifold dissection. This bijection is a natural generalisation from gentle to skew-gentle algebras, and it has also recently been shown in [Reference Amiot and Brüstle1, Reference He, Zhou and Zhu26]. However, in contrast to [Reference Amiot and Brüstle1], where derived equivalences between two skew-gentle algebras are studied in terms of diffeomorphisms of the orbifold working mostly in its double cover, we work directly in the orbifold and prove that graded curves in an orbifold dissection coming from a skew-gentle algebra are in bijection with homotopy strings and bands, which by [Reference Bekkert, Marcos and Merklen5] describe the indecomposable objects in the bounded derived category of the algebra. Furthermore, the data of the orbifold dissection contain, on the one hand, the data of a line field in the same way as for gentle algebras in [Reference Amiot and Brüstle1, Reference Amiot, Plamondon and Schroll3, Reference Lekili and Polishchuk32, Reference Opper, Plamondon and Schroll35], and on the other hand, the homological grading in the derived category. In this paper, we will focus on the latter.
Our results suggest that the bounded derived category of a skew-gentle algebra should in fact be a partially wrapped Fukaya category. However, in order to establish this, a complete description of the morphisms in the bounded derived category of a skew-gentle algebra is needed. Unlike for gentle algebras, in the skew-gentle case this is an open problem which we are hoping to address in a forthcoming paper [Reference Schroll and Valdivieso39].
We now state our first result. According to the classification in [Reference Bekkert, Marcos and Merklen5], indecomposable objects in the bounded derived category of a skew-gentle algebra fall within two classes, the so-called string objects and band objects, the latter coming in infinite families. Using this fact, we show the following.
Theorem A (Theorem 6.7) Let A be a skew-gentle algebra with associated surface O with orbifold points and induced orbifold dissection G. Denote by M the set of vertices of G. Then the data of (O, M, G) gives a geometric model for the objects of the bounded derived category
![]() $D^b(A)$
of A. More precisely,
$D^b(A)$
of A. More precisely,
-
(1) the indecomposable string objects in
 $D^b(A)$
are induced by graded arcs
$D^b(A)$
are induced by graded arcs
 $(\gamma, f)$
, where
$(\gamma, f)$
, where
 $\gamma$
is an orbifold homotopy class of curves in O that either start and end in marked points in M, or start in a marked point in M and wrap around a puncture at the other end, or wrap around a puncture at each end, and where f is a grading on
$\gamma$
is an orbifold homotopy class of curves in O that either start and end in marked points in M, or start in a marked point in M and wrap around a puncture at the other end, or wrap around a puncture at each end, and where f is a grading on
 $\gamma$
;
$\gamma$
; -
(2) each family of indecomposable band objects in
 $D^b(A)$
corresponds to a graded closed curve
$D^b(A)$
corresponds to a graded closed curve
 $(\gamma, f)$
where
$(\gamma, f)$
where
 $\gamma$
is an orbifold homotopy class of closed curves in O with grading f such that the combinatorial winding number induced by f is zero.
$\gamma$
is an orbifold homotopy class of closed curves in O with grading f such that the combinatorial winding number induced by f is zero.
We note that the combinatorial grading on curves naturally encodes the data of a line field on the orbifold surface.
Furthermore, we show that the orbifold dissection corresponding to a skew-gentle algebra encodes important information of the algebra itself. Namely, as an application of our geometric model, we show how the orbifold dissection associated with a skew-gentle algebra A encodes the singularity category of the A, its Gorenstein dimension and the derived invariant given by the q-Cartan matrix of A.
In [Reference Green21], Green introduced the notion of a strong Koszul algebra. By definition, an algebra is strong Koszul if it has a quadratic Gröbner basis. It is shown in [Reference Green and Huang19] that strong Koszul algebras are Koszul. However, there are examples of Koszul algebras which are not strong Koszul. One such example is the family of Sklyanin algebras [Reference Smith40].
We prove that skew-gentle algebras are strong Koszul and that their Koszul dual is again a (possibly infinite dimensional) skew-gentle algebra which can be realised on the same surface. More precisely, we show the following.
Theorem B (Theorem 4.8) Let A be a skew-gentle algebra. Then A is a strong Koszul algebra and its Koszul dual
![]() $A^!$
is (locally) skew-gentle, and A and
$A^!$
is (locally) skew-gentle, and A and
![]() $A^!$
give rise to dual orbifold dissections on the same surface with orbifold points.
$A^!$
give rise to dual orbifold dissections on the same surface with orbifold points.
2. Preliminaries
In this section, we fix some of the notation and definitions which will be used through this paper. We fix an algebraically closed field K of
![]() $\operatorname{char}\neq 2$
.
$\operatorname{char}\neq 2$
.
2.1. Gentle and skew-gentle algebras
In this subsection, we define gentle and skew-gentle algebras.
A quiver Q is a quadruple
![]() $(Q_0, Q_1, s, t)$
, where
$(Q_0, Q_1, s, t)$
, where
![]() $Q_0$
is the set of vertices,
$Q_0$
is the set of vertices,
![]() $Q_1$
is the set of arrows and
$Q_1$
is the set of arrows and
![]() $s, t:Q_1\to Q_0$
are functions indicating the source and target of an arrow. A path w of length
$s, t:Q_1\to Q_0$
are functions indicating the source and target of an arrow. A path w of length
![]() $n>0$
in Q is a sequence of arrows
$n>0$
in Q is a sequence of arrows
![]() $\alpha_1 \dots \alpha_n$
such that
$\alpha_1 \dots \alpha_n$
such that
![]() $t(\alpha_j)=s(\alpha_{j+1})$
for each
$t(\alpha_j)=s(\alpha_{j+1})$
for each
![]() $j=1, \dots, n-1$
. For each vertex i, we denote by
$j=1, \dots, n-1$
. For each vertex i, we denote by
![]() $e_i$
the trivial path of length 0.
$e_i$
the trivial path of length 0.
The path algebra KQ is defined as the K-vector space with basis the set of all paths in Q, with multiplication induced by concatenation of paths. A 2-sided ideal I of KQ is admissible if there exists an integer
![]() $m\geq 2$
such that
$m\geq 2$
such that
![]() $R^m \subset I \subset R^{2}$
, where R is the ideal of KQ generated by the arrows of Q.
$R^m \subset I \subset R^{2}$
, where R is the ideal of KQ generated by the arrows of Q.
Skew-gentle algebras were introduced in [Reference Geiß and de la Peña16]. They are closely linked to the well-studied class of gentle algebras. For instance, they are skew-group algebras of gentle algebras. They are of tame representation type [Reference Geiß and de la Peña16], and their derived categories are also tame [Reference Bekkert, Marcos and Merklen5, Reference Burban and Drozd12]. In [Reference Bekkert, Marcos and Merklen5], a combinatorial description of the indecomposable objects in the bounded derived category of a skew-gentle algebra is given in terms of homotopy strings and bands.
In order to define skew-gentle algebras, we first recall the definition of gentle algebras.
Definition 2.1 A K-algebra
![]() $\Lambda$
is gentle if it is Morita equivalent to
$\Lambda$
is gentle if it is Morita equivalent to
![]() $KQ/I$
, where
$KQ/I$
, where
-
(1) Q is a finite quiver such that for every vertex i of Q there are at most two arrows ending at i and at most two arrow starting at i;
-
(2) for every arrow
 $\alpha$
of Q, there is at most one arrow
$\alpha$
of Q, there is at most one arrow
 $\beta$
such that
$\beta$
such that
 $t(\alpha) = s(\beta)$
and
$t(\alpha) = s(\beta)$
and
 $\alpha\beta\in I$
, and there is at most one arrow
$\alpha\beta\in I$
, and there is at most one arrow
 $\gamma$
such that
$\gamma$
such that
 $t(\gamma) = s(\alpha)$
and
$t(\gamma) = s(\alpha)$
and
 $\gamma\alpha \in I$
;
$\gamma\alpha \in I$
; -
(3) for every arrow
 $\alpha$
of Q, there is at most one arrow
$\alpha$
of Q, there is at most one arrow
 $\beta'$
such that
$\beta'$
such that
 $\alpha\beta'\notin I$
, and there is at most one arrow
$\alpha\beta'\notin I$
, and there is at most one arrow
 $\gamma'$
such that
$\gamma'$
such that
 $\gamma'\alpha\not\in I$
;
$\gamma'\alpha\not\in I$
; -
(4) I is the 2-sided ideal of Q generated by certain paths of length 2;
-
(5) I is an admissible ideal of Q.
If I satisfies (1), (2), (3) and (4), then we say that the quotient
![]() $KQ/I$
is locally gentle.
$KQ/I$
is locally gentle.
Definition 2.2 A K-algebra A is (locally) skew-gentle if it is Morita equivalent to an algebra
![]() $KQ/I$
where
$KQ/I$
where
-
(1)
 $Q_1 = Q^{\prime}_1 \cup S$
, where for
$Q_1 = Q^{\prime}_1 \cup S$
, where for
 $\varepsilon \in S$
,
$\varepsilon \in S$
,
 $s(\varepsilon) = t(\varepsilon)$
,
$s(\varepsilon) = t(\varepsilon)$
, -
(2)
 $I = \langle I' \cup \{ \varepsilon^2 - \varepsilon \mid \varepsilon \in S\} \rangle$
,
$I = \langle I' \cup \{ \varepsilon^2 - \varepsilon \mid \varepsilon \in S\} \rangle$
, -
(3)
 $KQ' / I'$
is a (locally) gentle algebra where
$KQ' / I'$
is a (locally) gentle algebra where
 $Q' = (Q^{\prime}_1, Q_0)$
,
$Q' = (Q^{\prime}_1, Q_0)$
, -
(4) if
 $\varepsilon \in S$
then the vertex
$\varepsilon \in S$
then the vertex
 $i = s(\varepsilon)$
is the start or the end of exactly one arrow in
$i = s(\varepsilon)$
is the start or the end of exactly one arrow in
 $Q^{\prime}_1$
and if there is an arrow
$Q^{\prime}_1$
and if there is an arrow
 $\alpha \in Q^{\prime}_1$
with
$\alpha \in Q^{\prime}_1$
with
 $t(\alpha) = i$
and an arrow
$t(\alpha) = i$
and an arrow
 $\beta \in Q^{\prime}_1$
with
$\beta \in Q^{\prime}_1$
with
 $s(\beta) = i$
then
$s(\beta) = i$
then
 $\alpha \beta \in I'$
. Moreover, there is no other element in S starting at i.
$\alpha \beta \in I'$
. Moreover, there is no other element in S starting at i.
We call a vertex
![]() $i \in Q_0$
special if there exists
$i \in Q_0$
special if there exists
![]() $\varepsilon \in S$
such that
$\varepsilon \in S$
such that
![]() $i = s(\varepsilon)$
. We denote the set of special vertices by Sp. If
$i = s(\varepsilon)$
. We denote the set of special vertices by Sp. If
![]() $KQ/I$
is a skew-gentle algebra as above, we call (Q
$KQ/I$
is a skew-gentle algebra as above, we call (Q
![]() $^{\prime}$
, I
$^{\prime}$
, I
![]() $^{\prime}$
, Sp) a skew-gentle triple.
$^{\prime}$
, Sp) a skew-gentle triple.
Remark 2.3 If
![]() $KQ/I$
is a skew-gentle algebra with non-empty set of special vertices, then the ideal I is not admissible.
$KQ/I$
is a skew-gentle algebra with non-empty set of special vertices, then the ideal I is not admissible.
An admissible presentation
![]() $KQ^{sg} / I^{sg}$
of a skew-gentle algebra A is given as follows. Let
$KQ^{sg} / I^{sg}$
of a skew-gentle algebra A is given as follows. Let
![]() $\Lambda=KQ/I$
be the gentle algebra obtained from A by deleting the special loops.
$\Lambda=KQ/I$
be the gentle algebra obtained from A by deleting the special loops.
Set
 \begin{equation*}Q^{sg}_0(i) = \left\{\begin{array}{l@{\quad}l}\{i^+, i^-\} & \mbox{if $i \in Sp$} \\ \\[-7pt] \{ i \} & \mbox{otherwise} \\\end{array}.\right.\end{equation*}
\begin{equation*}Q^{sg}_0(i) = \left\{\begin{array}{l@{\quad}l}\{i^+, i^-\} & \mbox{if $i \in Sp$} \\ \\[-7pt] \{ i \} & \mbox{otherwise} \\\end{array}.\right.\end{equation*}
Define
The arrows of
![]() $Q_1^{sg}$
are defined as follows. The set
$Q_1^{sg}$
are defined as follows. The set
![]() $Q^{sg}_1[i, j]$
of arrows from vertex i to vertex j is given by
$Q^{sg}_1[i, j]$
of arrows from vertex i to vertex j is given by
The ideal
![]() $I^{sg}$
is defined as follows.
$I^{sg}$
is defined as follows.
 \begin{equation*}I^{sg}:=\left\langle \sum_{j\in Q_0^{sg}(s(\beta))}\lambda_j(i,\alpha, j)(j,\beta, k)\mid \alpha\beta\in I, i\in Q_0^{sg}(s(\alpha)), k\in Q_0^{sg}(t(\beta)) \right\rangle,\end{equation*}
\begin{equation*}I^{sg}:=\left\langle \sum_{j\in Q_0^{sg}(s(\beta))}\lambda_j(i,\alpha, j)(j,\beta, k)\mid \alpha\beta\in I, i\in Q_0^{sg}(s(\alpha)), k\in Q_0^{sg}(t(\beta)) \right\rangle,\end{equation*}
where
![]() $\lambda_j=-1$
if
$\lambda_j=-1$
if
![]() $j=l^-$
for some
$j=l^-$
for some
![]() $l\in Q_0$
, and
$l\in Q_0$
, and
![]() $\lambda_j=1$
otherwise.
$\lambda_j=1$
otherwise.
Note that in general, the relations in
![]() $I^{sg}$
are not monomial; instead, the ideal
$I^{sg}$
are not monomial; instead, the ideal
![]() $I^{sg}$
is admissible and quadratic.
$I^{sg}$
is admissible and quadratic.
Example 2.4 Consider the following quivers

and set
![]() $I=\{\varepsilon^2-\varepsilon\}$
and
$I=\{\varepsilon^2-\varepsilon\}$
and
![]() $I'=\{\varepsilon_1^2-\varepsilon_1,\varepsilon_2^2-\varepsilon_2, \alpha_1\alpha_2\}$
. Then, the algebras
$I'=\{\varepsilon_1^2-\varepsilon_1,\varepsilon_2^2-\varepsilon_2, \alpha_1\alpha_2\}$
. Then, the algebras
![]() $A_1=KQ/I$
and
$A_1=KQ/I$
and
![]() $A_2=KQ'/I'$
are skew-gentle and their respective admissible presentations
$A_2=KQ'/I'$
are skew-gentle and their respective admissible presentations
![]() $KQ^{sg}/I^{sg}$
and
$KQ^{sg}/I^{sg}$
and
![]() $KQ'^{sg}/I'^{sg}$
are as follows.
$KQ'^{sg}/I'^{sg}$
are as follows.
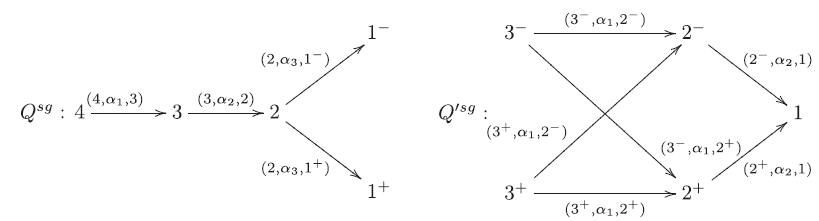
where
![]() $I^{sg}$
is the empty set and
$I^{sg}$
is the empty set and
Note that the algebra
![]() $KQ^{sg}/I^{sg} = KQ^{sg}$
corresponds to an orientation of the Dynkin diagram
$KQ^{sg}/I^{sg} = KQ^{sg}$
corresponds to an orientation of the Dynkin diagram
![]() $\mathbb{D}_5$
.
$\mathbb{D}_5$
.
2.2 Ribbon graphs and ribbon surfaces of a gentle algebra
We now briefly recall the construction of the ribbon graph of a gentle algebra embedded in a surface with boundary as introduced in [Reference Opper, Plamondon and Schroll35, Reference Schroll38] based on [Reference Schroll37].
A graph G is a quadruple
![]() $G=(M, E, s, \iota)$
, where M is a finite set of vertices, E a finite set of half-edges,
$G=(M, E, s, \iota)$
, where M is a finite set of vertices, E a finite set of half-edges,
![]() $s{:}E \to M$
is a function sending each half edge to the vertex it is attached to, and
$s{:}E \to M$
is a function sending each half edge to the vertex it is attached to, and
![]() $\iota{:}E \to E$
is a fixed point free involution sending each half-edge to the other half-edge it is glued to.
$\iota{:}E \to E$
is a fixed point free involution sending each half-edge to the other half-edge it is glued to.
A ribbon graph is a graph G endowed with a cyclic permutation of the half-edges at each vertex, given by a function
![]() $\sigma{:} E\to E$
whose orbits correspond to the sets
$\sigma{:} E\to E$
whose orbits correspond to the sets
![]() $s^{-1}(m)$
, for all
$s^{-1}(m)$
, for all
![]() $m\in M$
. A marked ribbon graph is a ribbon graph G equipped with a map
$m\in M$
. A marked ribbon graph is a ribbon graph G equipped with a map
![]() $p{:} M \to E$
, that is at each vertex we chose exactly one half-edge.
$p{:} M \to E$
, that is at each vertex we chose exactly one half-edge.
Let
![]() $\Lambda$
be a gentle algebra. Following [Reference Opper, Plamondon and Schroll35, Reference Schroll37, Reference Schroll38], we construct a marked ribbon graph
$\Lambda$
be a gentle algebra. Following [Reference Opper, Plamondon and Schroll35, Reference Schroll37, Reference Schroll38], we construct a marked ribbon graph
![]() $G_\Lambda$
canonically embedded into an unique, up to isomorphism, compact oriented surface
$G_\Lambda$
canonically embedded into an unique, up to isomorphism, compact oriented surface
![]() $S_\Lambda$
in such a way that the faces of
$S_\Lambda$
in such a way that the faces of
![]() $G_\Lambda$
are in bijection with the boundary components of
$G_\Lambda$
are in bijection with the boundary components of
![]() $S_\Lambda$
. Furthermore, the information given by m translates into a gluing of the vertices of
$S_\Lambda$
. Furthermore, the information given by m translates into a gluing of the vertices of
![]() $G_\Lambda$
onto the boundary components of
$G_\Lambda$
onto the boundary components of
![]() $S_\Lambda$
. More precisely,
$S_\Lambda$
. More precisely,
Definition 2.5 The marked ribbon graph
![]() $G_\Lambda$
of a gentle algebra
$G_\Lambda$
of a gentle algebra
![]() $\Lambda=KQ/I$
is defined as follows. The set of vertices M of
$\Lambda=KQ/I$
is defined as follows. The set of vertices M of
![]() $G_\Lambda$
are in bijection with the set consisting of
$G_\Lambda$
are in bijection with the set consisting of
-
• maximal paths in
 $KQ/I$
, that is, paths
$KQ/I$
, that is, paths
 $w \in KQ$
, with
$w \in KQ$
, with
 $w\notin I$
such that for any arrow
$w\notin I$
such that for any arrow
 $\alpha \in Q_1$
,
$\alpha \in Q_1$
,
 $\alpha w \in I$
and
$\alpha w \in I$
and
 $w\alpha \in I$
;
$w\alpha \in I$
; -
• trivial paths
 $e_i$
such that i is either the source or the target of only one arrow, or i is the target of exactly one arrow
$e_i$
such that i is either the source or the target of only one arrow, or i is the target of exactly one arrow
 $\alpha$
and the source of exactly one arrow
$\alpha$
and the source of exactly one arrow
 $\beta$
, and
$\beta$
, and
 $\alpha\beta\notin I$
;
$\alpha\beta\notin I$
;
The edges of
![]() $G_\Lambda$
are in bijection with the vertices of
$G_\Lambda$
are in bijection with the vertices of
![]() $Q_0$
: It follows from the definition of M that any vertex
$Q_0$
: It follows from the definition of M that any vertex
![]() $i \in Q_0$
is in exactly two elements of M, that is, there exist
$i \in Q_0$
is in exactly two elements of M, that is, there exist
![]() $w_1, w_2$
in M such that
$w_1, w_2$
in M such that
![]() $w_k = p_k e_i q_k$
for
$w_k = p_k e_i q_k$
for
![]() $p_k, q_k$
possibly trivial paths in Q and
$p_k, q_k$
possibly trivial paths in Q and
![]() $ k = 1,2$
. Hence by construction, every vertex in
$ k = 1,2$
. Hence by construction, every vertex in
![]() $Q_0$
corresponds to exactly two elements in M, thus defining an edge in
$Q_0$
corresponds to exactly two elements in M, thus defining an edge in
![]() $ G_\Lambda$
. Unless otherwise specified and if no confusion arises, we will denote the edge in
$ G_\Lambda$
. Unless otherwise specified and if no confusion arises, we will denote the edge in
![]() $G_\Lambda$
corresponding to the vertex
$G_\Lambda$
corresponding to the vertex
![]() $i \in Q_0$
again by i.
$i \in Q_0$
again by i.
Note that the construction of
![]() $G_\Lambda$
naturally gives a linear order of the half-edges attached to every vertex
$G_\Lambda$
naturally gives a linear order of the half-edges attached to every vertex
![]() $w \in M$
: namely, if
$w \in M$
: namely, if
![]() $i_1, \ldots, i_n$
are the half-edges at w then
$i_1, \ldots, i_n$
are the half-edges at w then
![]() $w = e_{i_1} \alpha_1 e_{i_2} \alpha_2 \cdots \alpha_{n-1} e_{i_n}$
, with
$w = e_{i_1} \alpha_1 e_{i_2} \alpha_2 \cdots \alpha_{n-1} e_{i_n}$
, with
![]() $\alpha_j \in Q_1$
and
$\alpha_j \in Q_1$
and
![]() $i_j \in Q_0$
and the induced linear order of the half-edges is given by
$i_j \in Q_0$
and the induced linear order of the half-edges is given by
![]() $i_1 < i_2 < \cdots < i_n$
. The cyclic order
$i_1 < i_2 < \cdots < i_n$
. The cyclic order
![]() $\sigma$
of the half-edges at w is then given by the cyclic closure of this linear order.
$\sigma$
of the half-edges at w is then given by the cyclic closure of this linear order.
Furthermore, we define the marking map
![]() $m{:} M \to E$
by
$m{:} M \to E$
by
![]() $m(w)=e_{e(w)}$
for
$m(w)=e_{e(w)}$
for
![]() $w \in M$
.
$w \in M$
.
We recall from [Reference Opper, Plamondon and Schroll35] the following definition.
Definition 2.6 The ribbon surface
![]() $S_\Lambda$
of a gentle algebra
$S_\Lambda$
of a gentle algebra
![]() $\Lambda$
is a tuple
$\Lambda$
is a tuple
![]() $S_\Lambda=(S_\Lambda, M_\Lambda)$
, where
$S_\Lambda=(S_\Lambda, M_\Lambda)$
, where
![]() $S_\Lambda$
is a compact oriented surface and a finite set
$S_\Lambda$
is a compact oriented surface and a finite set
![]() $M_\Lambda$
of marked points in the boundary of
$M_\Lambda$
of marked points in the boundary of
![]() $S_\Lambda$
such that
$S_\Lambda$
such that
![]() $G_\Lambda$
is canonically embedded into
$G_\Lambda$
is canonically embedded into
![]() $S_\Lambda$
with faces of
$S_\Lambda$
with faces of
![]() $G_\Lambda$
corresponding to boundary components in
$G_\Lambda$
corresponding to boundary components in
![]() $S_\Lambda$
and where
$S_\Lambda$
and where
![]() $M_\Lambda$
corresponds to the vertices
$M_\Lambda$
corresponds to the vertices
![]() $(G_\Lambda)_0$
of
$(G_\Lambda)_0$
of
![]() $G_\Lambda$
such that for each vertex
$G_\Lambda$
such that for each vertex
![]() $v\in V$
, the boundary component lies between m(v) and
$v\in V$
, the boundary component lies between m(v) and
![]() $\sigma(m(v))$
in the orientation of the surface.
$\sigma(m(v))$
in the orientation of the surface.
Remark 2.7 By [Reference Opper, Plamondon and Schroll35, Proposition 1.12], the ribbon graph
![]() $G_\Lambda$
of gentle algebra
$G_\Lambda$
of gentle algebra
![]() $\Lambda$
divides
$\Lambda$
divides
![]() $S_\Lambda$
into polygons of the following type
$S_\Lambda$
into polygons of the following type
-
(1) polygons whose edges are edges of
 $G_\Lambda$
except for exactly one boundary edge and whose interior contains no boundary component of
$G_\Lambda$
except for exactly one boundary edge and whose interior contains no boundary component of
 $S_\Lambda$
;
$S_\Lambda$
; -
(2) polygons whose edges are edges of
 $G_\Lambda$
and whose interior contains exactly one boundary component of
$G_\Lambda$
and whose interior contains exactly one boundary component of
 $S_\Lambda$
with no marked points.
$S_\Lambda$
with no marked points.
We refer to
![]() $(S_\Lambda,M_\Lambda, G_{\Lambda})$
as the surface dissection of
$(S_\Lambda,M_\Lambda, G_{\Lambda})$
as the surface dissection of
![]() $S_\Lambda$
associated with the gentle algebra
$S_\Lambda$
associated with the gentle algebra
![]() $\Lambda$
. In the following, we will replace any boundary component with no marked points, such as those in Remark 2.7 (2), with punctures. Furthermore, by abuse of notation we will sometimes treat these punctures as marked points in the interior of the surface.
$\Lambda$
. In the following, we will replace any boundary component with no marked points, such as those in Remark 2.7 (2), with punctures. Furthermore, by abuse of notation we will sometimes treat these punctures as marked points in the interior of the surface.
3. Skew-gentle algebras and orbifolds
In this section, we define a graph associated with a skew-gentle algebra generalising the ribbon graph associated with a gentle algebra, and we will show that this graph also has a canonical embedding into a surface.
Lemma 3.1 Let A be a skew-gentle algebra,
![]() $\Lambda=KQ/I$
be the associated gentle algebra obtained from A by deleting all special loops and
$\Lambda=KQ/I$
be the associated gentle algebra obtained from A by deleting all special loops and
![]() $(S_\Lambda,M_\Lambda, G_{\Lambda})$
be its surface dissection. Then any special vertex
$(S_\Lambda,M_\Lambda, G_{\Lambda})$
be its surface dissection. Then any special vertex
![]() $i\in Sp$
corresponds to an edge g in
$i\in Sp$
corresponds to an edge g in
![]() $G_{\Lambda}$
of a digon with exactly one boundary edge and whose interior contains no boundary component of
$G_{\Lambda}$
of a digon with exactly one boundary edge and whose interior contains no boundary component of
![]() $S_\Lambda$
.
$S_\Lambda$
.
Proof. Let i be a special vertex of A corresponding the edge i in
![]() $G_\Lambda$
and let P and P
$G_\Lambda$
and let P and P
![]() $^{\prime}$
be the polygons sharing the edge g. By Definition 2.2, the vertex i is either the start or the end of exactly one arrow in Q or there are exactly two arrows
$^{\prime}$
be the polygons sharing the edge g. By Definition 2.2, the vertex i is either the start or the end of exactly one arrow in Q or there are exactly two arrows
![]() $\alpha, \beta$
in Q such that
$\alpha, \beta$
in Q such that
![]() $s(\beta)=t(\alpha)=i$
and
$s(\beta)=t(\alpha)=i$
and
![]() $\alpha\beta\in I$
.
$\alpha\beta\in I$
.
Suppose first that we are in the latter case, that is that there are exactly two arrows
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
such that
$\beta$
such that
![]() $s(\beta)=t(\alpha)=i$
. Assume further that
$s(\beta)=t(\alpha)=i$
. Assume further that
![]() $s(\alpha) $
and
$s(\alpha) $
and
![]() $t(\beta)$
are edges in P. Then, the edge j of P
$t(\beta)$
are edges in P. Then, the edge j of P
![]() $^{\prime}$
preceding i and the edge k following i in the orientation of
$^{\prime}$
preceding i and the edge k following i in the orientation of
![]() $S_\Lambda$
are boundary edges. By,[Reference Opper, Plamondon and Schroll35, Proposition 1.12], every polygon in the surface dissection of
$S_\Lambda$
are boundary edges. By,[Reference Opper, Plamondon and Schroll35, Proposition 1.12], every polygon in the surface dissection of
![]() $S_\Lambda$
has at most one boundary edge which implies that
$S_\Lambda$
has at most one boundary edge which implies that
![]() $j=k$
and P
$j=k$
and P
![]() $^{\prime}$
is a digon.
$^{\prime}$
is a digon.
In the case that there is exactly one arrow incident with i, the argument is similar.
We now give the definition of a generalised ribbon graph associated with a skew-gentle algebra based on the ribbon graph and surface of the underlying gentle algebra.
Let A be a skew-gentle,
![]() $\Lambda=KQ/I$
be the associated gentle algebra obtained from A by deleting all special vertices, and let
$\Lambda=KQ/I$
be the associated gentle algebra obtained from A by deleting all special vertices, and let
![]() $(S_\Lambda, M_\Lambda, G_\Lambda)$
its surface dissection. For each edge g of
$(S_\Lambda, M_\Lambda, G_\Lambda)$
its surface dissection. For each edge g of
![]() $G_{\Lambda}$
corresponding to a special vertex
$G_{\Lambda}$
corresponding to a special vertex
![]() $i\in Sp$
, let P and P
$i\in Sp$
, let P and P
![]() $^{\prime}$
be the polygons sharing the edge g. Suppose further that P
$^{\prime}$
be the polygons sharing the edge g. Suppose further that P
![]() $^{\prime}$
is a digon with one boundary edge (which exists by the specialness of v, see Lemma 3.1). We define the local replacement of g in
$^{\prime}$
is a digon with one boundary edge (which exists by the specialness of v, see Lemma 3.1). We define the local replacement of g in
![]() $G_\Lambda$
as the graph embedded graph
$G_\Lambda$
as the graph embedded graph
![]() $G^{\prime}_{\Lambda}$
obtained by contracting the boundary segment of P
$G^{\prime}_{\Lambda}$
obtained by contracting the boundary segment of P
![]() $^{\prime}$
and identifying the vertices
$^{\prime}$
and identifying the vertices
![]() $p_1$
and
$p_1$
and
![]() $p_2$
by collapsing the interior of the polygon P
$p_2$
by collapsing the interior of the polygon P
![]() $^{\prime}$
so that g is incident with
$^{\prime}$
so that g is incident with
![]() $p_1 = p_2$
. In the process, we obtain a new marked point in the interior of P, we will denote this point by o and depict by drawing a cross-shaped vertex in the surface. We will refer to these vertices as special vertices. We locally illustrate the local replacement and the resulting new vertex in Figure 1.
$p_1 = p_2$
. In the process, we obtain a new marked point in the interior of P, we will denote this point by o and depict by drawing a cross-shaped vertex in the surface. We will refer to these vertices as special vertices. We locally illustrate the local replacement and the resulting new vertex in Figure 1.

Figure 1. A local replacement.
Remark 3.2 (1) Observe that after local replacement the polygon P is no longer a polygon, but corresponds to a degenerate or self-folded polygon with a special edge ending in a cross-shaped vertex.
(2) We note that up to homeomorphism the surface does not change under local replacement. However, the number of marked points in the boundary changes.
Definition 3.3 Let A be a skew-gentle algebra,
![]() $\Lambda=KQ/I$
be the associated gentle algebra obtained from A by deleting all special vertices, and
$\Lambda=KQ/I$
be the associated gentle algebra obtained from A by deleting all special vertices, and
![]() $(S_\Lambda, M_{\Lambda}, G_{\Lambda})$
be its surface dissection.
$(S_\Lambda, M_{\Lambda}, G_{\Lambda})$
be its surface dissection.
The generalised ribbon graph
![]() $G_A$
of A is the graph obtained from
$G_A$
of A is the graph obtained from
![]() $G_\Lambda$
by applying a local replacement at each special vertex.
$G_\Lambda$
by applying a local replacement at each special vertex.
Denote by
![]() $M_A$
the marked points on
$M_A$
the marked points on
![]() $S_\Lambda$
corresponding to the vertices of the embedded ribbon graph
$S_\Lambda$
corresponding to the vertices of the embedded ribbon graph
![]() $G_A$
which are not special. Let
$G_A$
which are not special. Let
![]() $O_A=(S, M_A, \mathcal{O})$
be the triple given by the surface
$O_A=(S, M_A, \mathcal{O})$
be the triple given by the surface
![]() $S = S_\Lambda$
, the marked points
$S = S_\Lambda$
, the marked points
![]() $M_A$
and the set of special vertices
$M_A$
and the set of special vertices
![]() $\mathcal{O}$
.
$\mathcal{O}$
.
From now on, consider the special vertices of
![]() $G_A$
to be orbifold points of order two and we say that an edge in
$G_A$
to be orbifold points of order two and we say that an edge in
![]() $G_A$
joining a vertex and an orbifold point is a special edge. Consequently, we refer to
$G_A$
joining a vertex and an orbifold point is a special edge. Consequently, we refer to
![]() $O_A$
as the orbifold of A.
$O_A$
as the orbifold of A.
Note that the above construction also works for locally skew-gentle algebras
![]() $A = KQ/I$
. In this case, the generalised ribbon graph will have in addition to the special vertices punctures corresponding to either cycles with no relations in the quiver or to cycles with full relations, but with a special loop at each vertex of the cycle.
$A = KQ/I$
. In this case, the generalised ribbon graph will have in addition to the special vertices punctures corresponding to either cycles with no relations in the quiver or to cycles with full relations, but with a special loop at each vertex of the cycle.
Remark 3.4 We note that we can construct the generalised ribbon graph directly from the data of (Q, I, Sp), where
![]() $A = KQ/I$
is a skew-gentle algebra with set of special vertices Sp. We say that a path p in Q is Sp-maximal if for all
$A = KQ/I$
is a skew-gentle algebra with set of special vertices Sp. We say that a path p in Q is Sp-maximal if for all
![]() $x \in Q_1\setminus Sp$
we have
$x \in Q_1\setminus Sp$
we have
![]() $px = xp = 0$
in
$px = xp = 0$
in
![]() $KQ/I$
. Then, the set of vertices M of the ribbon graph
$KQ/I$
. Then, the set of vertices M of the ribbon graph
![]() $G_A$
of A is in bijection with the union of all
$G_A$
of A is in bijection with the union of all
-
• Sp-maximal paths;
-
• trivial paths
 $e_i$
such that i is either the source or the target of only one arrow, or i is the target of exactly one arrow
$e_i$
such that i is either the source or the target of only one arrow, or i is the target of exactly one arrow
 $\alpha$
and the source of exactly one arrow
$\alpha$
and the source of exactly one arrow
 $\beta$
, and
$\beta$
, and
 $\alpha \beta \notin I$
, or
$\alpha \beta \notin I$
, or
 $i \in Sp$
.
$i \in Sp$
.
The set of edges of
![]() $G_A$
is in bijection with the vertices of
$G_A$
is in bijection with the vertices of
![]() $Q_0$
(note that this includes the special vertices). Then,
$Q_0$
(note that this includes the special vertices). Then,
![]() $G_A$
is a ribbon graph with the cyclic ordering of the edges at each vertex induced by the Sp-maximal paths. Denote by
$G_A$
is a ribbon graph with the cyclic ordering of the edges at each vertex induced by the Sp-maximal paths. Denote by
![]() $S_A$
the corresponding oriented surface with boundary such that
$S_A$
the corresponding oriented surface with boundary such that
![]() $G_A$
is a deformation retract of
$G_A$
is a deformation retract of
![]() $S_\Lambda$
. Now define a marking map
$S_\Lambda$
. Now define a marking map
![]() $m{:} M\setminus Sp \to E$
similar to the gentle case. Note that the elements of M corresponding to the idempotents at special vertices in
$m{:} M\setminus Sp \to E$
similar to the gentle case. Note that the elements of M corresponding to the idempotents at special vertices in
![]() $Q_0$
are not marked. The marking map gives a unique way of gluing the marked vertices of
$Q_0$
are not marked. The marking map gives a unique way of gluing the marked vertices of
![]() $G_A$
to the boundary of
$G_A$
to the boundary of
![]() $S_A$
whereas the vertices of
$S_A$
whereas the vertices of
![]() $G_A$
corresponding to elements in Sp stay in the interior of the surface where they give rise to the set
$G_A$
corresponding to elements in Sp stay in the interior of the surface where they give rise to the set
![]() $\mathcal O$
of orbifold points of order two. This gives rise to a generalised surface dissection which coincides with the construction of the orbifold dissection of
$\mathcal O$
of orbifold points of order two. This gives rise to a generalised surface dissection which coincides with the construction of the orbifold dissection of
![]() $O_A$
in Definition 3.7 below.
$O_A$
in Definition 3.7 below.
Example 3.5 Let
![]() $A_1=KQ/I$
and
$A_1=KQ/I$
and
![]() $A_2=KQ'/I'$
be the skew-gentle algebras from Example 2.4. Note that the set of vertices
$A_2=KQ'/I'$
be the skew-gentle algebras from Example 2.4. Note that the set of vertices
![]() ${M}_{A_1}$
of the generalised ribbon graph
${M}_{A_1}$
of the generalised ribbon graph
![]() $G_{A_1}$
is the set
$G_{A_1}$
is the set
![]() $\{\alpha_1\alpha_2\alpha_3\varepsilon, e_4, e_3, e_2, e_1\}$
where
$\{\alpha_1\alpha_2\alpha_3\varepsilon, e_4, e_3, e_2, e_1\}$
where
![]() $e_1$
corresponds to the trivial path associated with the special vertex 1 and that the set of vertices
$e_1$
corresponds to the trivial path associated with the special vertex 1 and that the set of vertices
![]() $M_{A_2}$
of
$M_{A_2}$
of
![]() $A_2$
is the set
$A_2$
is the set
![]() $\{\varepsilon_1\alpha_1\varepsilon_2\alpha_2, e_3, e_2, e_1\}$
where
$\{\varepsilon_1\alpha_1\varepsilon_2\alpha_2, e_3, e_2, e_1\}$
where
![]() $e_3$
and
$e_3$
and
![]() $e_2$
correspond to the trivial path associated with the special vertices 3 and 2 respectively. The generalised ribbon graphs
$e_2$
correspond to the trivial path associated with the special vertices 3 and 2 respectively. The generalised ribbon graphs
![]() $G_{A_1}$
and
$G_{A_1}$
and
![]() $G_{A_2}$
can be seen in Figure 2.
$G_{A_2}$
can be seen in Figure 2.

Figure 2. Generalised ribbon graphs of
![]() $\mathbb D_5$
and
$\mathbb D_5$
and
![]() $A_2$
from Example 2.4.
$A_2$
from Example 2.4.
Then, the generalised ribbon graphs
![]() $G_{A_1}$
and
$G_{A_1}$
and
![]() $G_{A_2}$
embedded in their respective orbifolds can be seen in Figure 3.
$G_{A_2}$
embedded in their respective orbifolds can be seen in Figure 3.

Figure 3. Generalised ribbon graphs of
![]() $\mathbb D_5$
and
$\mathbb D_5$
and
![]() $KQ'/ I$
from Example 2.4 embedded in their respective orbifolds.
$KQ'/ I$
from Example 2.4 embedded in their respective orbifolds.
For any skew-gentle algebra A, the edges of
![]() $G_A$
cut the orbifold
$G_A$
cut the orbifold
![]() $O_A$
into polygons, some of which contain the points in
$O_A$
into polygons, some of which contain the points in
![]() $\mathcal{O}$
and a special edge connected to them. We call those polygons degenerate polygons. We note that the following two results, Proposition 3.6 and Theorem 3.8, have independently appeared in [Reference Amiot and Brüstle1].
$\mathcal{O}$
and a special edge connected to them. We call those polygons degenerate polygons. We note that the following two results, Proposition 3.6 and Theorem 3.8, have independently appeared in [Reference Amiot and Brüstle1].
Proposition 3.6 Let A be a skew-gentle algebra, and let
![]() $G_A$
be the generalised ribbon graph of A embedded into its orbifold
$G_A$
be the generalised ribbon graph of A embedded into its orbifold
![]() $O_A=(S_A, M_A, \mathcal{O})$
. Then
$O_A=(S_A, M_A, \mathcal{O})$
. Then
![]() $G_A$
cuts
$G_A$
cuts
![]() $O_A$
into four types of polygons:
$O_A$
into four types of polygons:
-
(a) polygons and degenerate polygons containing exactly one boundary segment whose interior contains no boundary component of
 $O_A$
.
$O_A$
. -
(b) polygons and degenerate polygons with no boundary segments and whose interior contains exactly one boundary component of
 $O_A$
with no marked points.
$O_A$
with no marked points.
Proof. This directly follows from [Reference Opper, Plamondon and Schroll35, Proposition 1.12] and the construction of
![]() $G_A$
by local replacement.
$G_A$
by local replacement.
Definition 3.7 We call an orbifold dissection any tuple of the form
![]() $(S,M,\mathcal O, G)$
, where S is a compact oriented surface with marked points M, orbifold points
$(S,M,\mathcal O, G)$
, where S is a compact oriented surface with marked points M, orbifold points
![]() $\mathcal{O}$
of order 2 and G is a graph as in Remark 3.4 dissecting S into polygons and degenerate polygons of the form as described in Proposition 3.6.
$\mathcal{O}$
of order 2 and G is a graph as in Remark 3.4 dissecting S into polygons and degenerate polygons of the form as described in Proposition 3.6.
Before stating the next result, we define the following notation. Denote by B one of the skew-gentle algebras with two vertices, one arrow between them and one or two special loops.
Theorem 3.8 Every skew-gentle algebra non-isomorphic to B uniquely determines an orbifold dissection up to homeomorphism and every orbifold dissection uniquely determines a skew-gentle algebra.
Proof. By Proposition 3.6, it is enough to show that given a orbifold dissection
![]() $(S,M,\mathcal O, G)$
there exists a skew-gentle algebra A having
$(S,M,\mathcal O, G)$
there exists a skew-gentle algebra A having
![]() $(S,M,\mathcal{O})$
as its orbifold and G as its generalised ribbon graph. Given
$(S,M,\mathcal{O})$
as its orbifold and G as its generalised ribbon graph. Given
![]() $(S,M, \mathcal{O}, G)$
, define a quiver Q as follows:
$(S,M, \mathcal{O}, G)$
, define a quiver Q as follows:
-
(1) the vertices of Q are in bijection with the edges of G;
-
(2) if i, j are two edges incident with the same vertex in G then there is an arrow from i to j if j is a direct successor of i in the orientation of the surface, that is there is no other edge of G between i and j. Note that if i is a special edge in a degenerate polygon, then i is its own successor, therefore there is a loop incident to i. Denote by Sp the set of vertices of Q which corresponds to the special edges of G and by S the set of special loops incident to a special vertex
 $i\in Sp$
.
$i\in Sp$
.
Observe that by construction any vertex of Q has at most two in going arrows and at most two outgoing arrows, because any edge of G shares at most two (degenerate) polygons. Let I be the ideal of KQ generated by the following relations: if
![]() $\alpha{:} i \to j$
and
$\alpha{:} i \to j$
and
![]() $\beta{:}j\to k$
are two consecutive arrows such that i, j and k correspond to edges of the same (degenerate) polygon and such that neither
$\beta{:}j\to k$
are two consecutive arrows such that i, j and k correspond to edges of the same (degenerate) polygon and such that neither
![]() $\alpha$
nor
$\alpha$
nor
![]() $\beta$
correspond to a special loop, then
$\beta$
correspond to a special loop, then
![]() $\alpha\beta$
is a relation. Consequently, for any arrow
$\alpha\beta$
is a relation. Consequently, for any arrow
![]() $\alpha$
, there is at most one consecutive arrow
$\alpha$
, there is at most one consecutive arrow
![]() $\beta$
such that
$\beta$
such that
![]() $\alpha\beta\in I$
and at most one preceding arrow
$\alpha\beta\in I$
and at most one preceding arrow
![]() $\gamma$
such that
$\gamma$
such that
![]() $\gamma\alpha\in I$
. Finally, for each loop
$\gamma\alpha\in I$
. Finally, for each loop
![]() $\varepsilon$
, incident to a special vertex,
$\varepsilon$
, incident to a special vertex,
![]() $\varepsilon^2-\varepsilon\in I$
.
$\varepsilon^2-\varepsilon\in I$
.
We need to show that
![]() $A=KQ/I$
is a skew-gentle algebra. By construction, if P is a degenerate polygon, and v is a special edge of P, then the valency of i is at most two, because any special edge belongs to exactly one degenerate polygon. Moreover, if the valency of i is two, by the definition of the generators of I, the composition of the arrow ending at i with the arrow starting at i is a generator.
$A=KQ/I$
is a skew-gentle algebra. By construction, if P is a degenerate polygon, and v is a special edge of P, then the valency of i is at most two, because any special edge belongs to exactly one degenerate polygon. Moreover, if the valency of i is two, by the definition of the generators of I, the composition of the arrow ending at i with the arrow starting at i is a generator.
Finally, it follows from the construction of
![]() $KQ/I$
that its orbifold dissection is
$KQ/I$
that its orbifold dissection is
![]() $(S,M, \mathcal{O}, G)$
.
$(S,M, \mathcal{O}, G)$
.
4. The dual graph and the Koszul dual of a skew-gentle algebra
In this subsection, we show that a skew-gentle algebra is strong Koszul and that its Koszul dual is again skew-gentle. Furthermore, given a skew-gentle algebra A and the corresponding skew orbifold dissection, we construct a dual graph embedded in the orbifold and we show that this dual graph is the orbifold dissection of the Koszul dual of A.
According to [Reference Green21], an algebra
![]() $KQ/I$
is strong Koszul if I is quadratic and has a quadratic Gröbner basis. By [Reference Green and Huang19], any strong Koszul algebra is a Koszul algebra, but the converse does not always hold, for example, Sklyanin algebras [Reference Smith40] are Koszul algebras but not strong Koszul.
$KQ/I$
is strong Koszul if I is quadratic and has a quadratic Gröbner basis. By [Reference Green and Huang19], any strong Koszul algebra is a Koszul algebra, but the converse does not always hold, for example, Sklyanin algebras [Reference Smith40] are Koszul algebras but not strong Koszul.
Since gentle algebras are Koszul and since skew-group constructions preserve the Koszul property [Reference Li33], it is clear that skew-gentle algebras are Koszul. However, it is not known whether the skew-group algebra of a strong Koszul algebra is strong Koszul. The aim of this section is prove that skew-gentle algebras are strong Koszul. As a consequence, we also give a new proof that skew-gentle algebras are Koszul. Following [Reference Green20, Reference Green, Hille and Schroll22], we recall the basic definitions of Gröbner bases. Recall that
![]() $\succ$
is an admissible order on B if
$\succ$
is an admissible order on B if
![]() $\succ$
is a total order on B such that every non-empty subset of B has a minimal element, and
$\succ$
is a total order on B such that every non-empty subset of B has a minimal element, and
![]() $\succ$
is compatible with the multiplicative structure of B, namely the following conditions hold for any
$\succ$
is compatible with the multiplicative structure of B, namely the following conditions hold for any
![]() $p,q,x,w \in B$
, see [Reference Green20, Section 2.2.1] for details.
$p,q,x,w \in B$
, see [Reference Green20, Section 2.2.1] for details.
-
(1) if
 $p\succ q$
then
$p\succ q$
then
 $px\succ qx$
when
$px\succ qx$
when
 $px\neq 0$
and
$px\neq 0$
and
 $qx\neq 0$
.
$qx\neq 0$
. -
(2) if
 $p\succ q$
then
$p\succ q$
then
 $wp\succ wq$
when
$wp\succ wq$
when
 $px\neq 0$
and
$px\neq 0$
and
 $qx\neq 0$
.
$qx\neq 0$
. -
(3) if
 $p=qx$
, then
$p=qx$
, then
 $p\succ q$
and
$p\succ q$
and
 $p\succ x$
.
$p\succ x$
.
Definition 4.1 Let Q be a quiver,
![]() $\mathcal B$
the basis of paths of KQ and
$\mathcal B$
the basis of paths of KQ and
![]() $\succ$
an admissible order on
$\succ$
an admissible order on
![]() $\mathcal{B}$
. For
$\mathcal{B}$
. For
![]() $x=\sum_{p\in \mathcal B}\lambda_p p$
with
$x=\sum_{p\in \mathcal B}\lambda_p p$
with
![]() $\lambda_p\in K$
such that almost all
$\lambda_p\in K$
such that almost all
![]() $\lambda_p=0$
define the tip of x to be
$\lambda_p=0$
define the tip of x to be
![]() $\operatorname{tip}(x)=p \textrm{ if } \lambda_p\neq 0 \textrm{ and } p {\succ} q \textrm{ for all } q \textrm{ with } \lambda_p\neq 0.$
Furthermore, if
$\operatorname{tip}(x)=p \textrm{ if } \lambda_p\neq 0 \textrm{ and } p {\succ} q \textrm{ for all } q \textrm{ with } \lambda_p\neq 0.$
Furthermore, if
![]() $X\subset KQ$
then we define
$X\subset KQ$
then we define
![]() $\operatorname{tip}(X)=\{\operatorname{tip}(x)\mid x\in X\setminus\{0\}\}$
.
$\operatorname{tip}(X)=\{\operatorname{tip}(x)\mid x\in X\setminus\{0\}\}$
.
To simplify notation, in this section a vertex idempotent
![]() $e_i$
associated with a vertex i will be denoted by i. An element
$e_i$
associated with a vertex i will be denoted by i. An element
![]() $x\in KQ$
is uniform if there are vertices
$x\in KQ$
is uniform if there are vertices
![]() $i, j\in Q_0$
such that
$i, j\in Q_0$
such that
![]() $ixj = x$
.
$ixj = x$
.
Definition 4.2 Let
![]() $KQ/I$
be an algebra and let
$KQ/I$
be an algebra and let
![]() $\succ$
be an admissible order on the basis of paths
$\succ$
be an admissible order on the basis of paths
![]() $\mathcal{B}$
of KQ. We say that
$\mathcal{B}$
of KQ. We say that
![]() $\mathcal{G} \subset I$
is a Gröbner basis for I with respect
$\mathcal{G} \subset I$
is a Gröbner basis for I with respect
![]() $\succ$
if
$\succ$
if
![]() $\mathcal{G}$
is a set of uniform elements in I such that
$\mathcal{G}$
is a set of uniform elements in I such that
![]() $\langle \operatorname{tip}(I)\rangle = \langle \operatorname{tip}(\mathcal{G})\rangle$
.
$\langle \operatorname{tip}(I)\rangle = \langle \operatorname{tip}(\mathcal{G})\rangle$
.
The concepts of simple and complete reductions play an important role in Gröbner basis theory. For example, a useful characterisation of a Gröbner basis is that all its elements completely reduce to zero, see, for example, [Reference Green, Hille and Schroll22, Proposition 2.9]. Furthermore, complete reduction can be used to complete a subset
![]() $\mathcal{H}$
of uniform elements of the ideal I to a Gröbner basis.
$\mathcal{H}$
of uniform elements of the ideal I to a Gröbner basis.
Definition 4.3 Let
![]() $\mathcal H$
be a set of nonzero uniform elements in KQ and
$\mathcal H$
be a set of nonzero uniform elements in KQ and
![]() $x =\sum_{p\in \mathcal B}\lambda_p p\neq 0$
be an element of KQ with
$x =\sum_{p\in \mathcal B}\lambda_p p\neq 0$
be an element of KQ with
![]() $\lambda_p \in K$
.
$\lambda_p \in K$
.
-
• A simple reduction of x by
 $\mathcal H$
is defined as follows: Suppose for some p with
$\mathcal H$
is defined as follows: Suppose for some p with
 $\lambda_p\neq 0$
there exists
$\lambda_p\neq 0$
there exists
 $h \in \mathcal H$
and
$h \in \mathcal H$
and
 $r,s \in \mathcal{B}$
such that
$r,s \in \mathcal{B}$
such that
 $r \operatorname{tip}(h) s = p$
. If
$r \operatorname{tip}(h) s = p$
. If
 $\lambda$
is the coefficient of
$\lambda$
is the coefficient of
 $\operatorname{tip}(h)$
as a summand of h as a linear combination of basic elements then a simple reduction
$\operatorname{tip}(h)$
as a summand of h as a linear combination of basic elements then a simple reduction
 $x \to_{\mathcal H} y$
of x by
$x \to_{\mathcal H} y$
of x by
 $\mathcal H$
is
$\mathcal H$
is
 $y = \lambda x-\lambda_p rhs$
. This replaces
$y = \lambda x-\lambda_p rhs$
. This replaces
 $\lambda_p p$
in x by a linear combination of paths smaller than p.
$\lambda_p p$
in x by a linear combination of paths smaller than p. -
• A complete reduction
 $x {\implies}_{\mathcal H} y_n$
of x by
$x {\implies}_{\mathcal H} y_n$
of x by
 $\mathcal H$
is a sequence of simple reductions
$\mathcal H$
is a sequence of simple reductions
 $(\dots((x \to_{\mathcal H} y_1) \to_{\mathcal H} y_2) \to_{\mathcal H} \dots) \to_{\mathcal H} y_n$
, such that either
$(\dots((x \to_{\mathcal H} y_1) \to_{\mathcal H} y_2) \to_{\mathcal H} \dots) \to_{\mathcal H} y_n$
, such that either
 $y_n = 0$
or
$y_n = 0$
or
 $y_n$
has no simple reductions by H.
$y_n$
has no simple reductions by H.
Definition 4.4 Let
![]() $x = \sum_{p\in \mathcal B}\lambda_pp$
and
$x = \sum_{p\in \mathcal B}\lambda_pp$
and
![]() $y=\sum_{q\in\mathcal B}\mu_qq$
in KQ. Suppose that
$y=\sum_{q\in\mathcal B}\mu_qq$
in KQ. Suppose that
![]() $s = \operatorname{tip}(x), t= \operatorname{tip}(y)$
and
$s = \operatorname{tip}(x), t= \operatorname{tip}(y)$
and
![]() $sm = nt$
for some
$sm = nt$
for some
![]() $m, n \in \mathcal B \setminus Q_0$
where the lengths of m and n are strictly less than the length of s. Then the overlap relation,
$m, n \in \mathcal B \setminus Q_0$
where the lengths of m and n are strictly less than the length of s. Then the overlap relation,
![]() $\mathbf {o}(x, y, m, n)$
, is
$\mathbf {o}(x, y, m, n)$
, is
We now show that a skew-gentle algebra is strongly Koszul by showing that it has a quadratic Gröbner basis. For this, we begin by showing that given a skew-gentle algebra A, any admissible order for the underlying gentle algebra
![]() $\Lambda$
induces a natural admissible order for A.
$\Lambda$
induces a natural admissible order for A.
Lemma 4.5 Let A be a skew-gentle,
![]() $\Lambda=KQ/I$
be the gentle algebra obtaining from A by deleting special loops, and let
$\Lambda=KQ/I$
be the gentle algebra obtaining from A by deleting special loops, and let
![]() $\mathcal{B}$
be the basis of paths of KQ. Suppose that
$\mathcal{B}$
be the basis of paths of KQ. Suppose that
![]() $\succ_Q$
is an admissible order on
$\succ_Q$
is an admissible order on
![]() $\mathcal{B}$
. Then
$\mathcal{B}$
. Then
![]() $\succ_Q$
induces an admissible order
$\succ_Q$
induces an admissible order
![]() $\succ$
on the basis of paths
$\succ$
on the basis of paths
![]() $\mathcal{B}^{sg}$
of
$\mathcal{B}^{sg}$
of
![]() $KQ^{sg}$
.
$KQ^{sg}$
.
Proof. Let
![]() $\succ_{Q}$
be an order on Q inducing an admissible order on
$\succ_{Q}$
be an order on Q inducing an admissible order on
![]() $\mathcal{B}$
. Consider
$\mathcal{B}$
. Consider
![]() $\succ$
an order on
$\succ$
an order on
![]() $Q^{sg}$
induced by
$Q^{sg}$
induced by
![]() $\succ_{Q}$
as follows.
$\succ_{Q}$
as follows.
Let
![]() $(i, \alpha, j)$
and
$(i, \alpha, j)$
and
![]() $(i', \beta, j')$
be two arrows in
$(i', \beta, j')$
be two arrows in
![]() $Q^{sg}$
. If
$Q^{sg}$
. If
![]() $\alpha\neq \beta$
, we say that
$\alpha\neq \beta$
, we say that
![]() $(i, \alpha, j)\succ (i', \beta, j')$
if and only if
$(i, \alpha, j)\succ (i', \beta, j')$
if and only if
![]() $\alpha \succ_Q \beta$
.
$\alpha \succ_Q \beta$
.
Now, suppose that
![]() $\alpha=\beta$
and
$\alpha=\beta$
and
![]() $s(\alpha)$
or
$s(\alpha)$
or
![]() $t(\alpha)$
is a special vertex, then we fix an order on the set of arrows induced by
$t(\alpha)$
is a special vertex, then we fix an order on the set of arrows induced by
![]() $\alpha{:}i \to j$
as follows.
$\alpha{:}i \to j$
as follows.
If i and j are special vertices, then
![]() $(i^+, \alpha, j^+) \succ (i^-,\alpha, j^-) \succ (i^+, \alpha, j^-) \succ (i^-, \alpha, j^+)$
. If i is a special vertex and
$(i^+, \alpha, j^+) \succ (i^-,\alpha, j^-) \succ (i^+, \alpha, j^-) \succ (i^-, \alpha, j^+)$
. If i is a special vertex and
![]() $t(\alpha)$
is not special (resp. i is not special and j is special), then
$t(\alpha)$
is not special (resp. i is not special and j is special), then
![]() $(i^+, \alpha, j) \succ (i^-,\alpha, j)$
(resp.
$(i^+, \alpha, j) \succ (i^-,\alpha, j)$
(resp.
![]() $(i, \alpha, j^+) \succ (i,\alpha, j^-)$
).
$(i, \alpha, j^+) \succ (i,\alpha, j^-)$
).
By construction, the only property we need to check in order for
![]() $\succ$
to be admissible, is that every descending chain in
$\succ$
to be admissible, is that every descending chain in
![]() $\mathcal{B}^{sg}$
has a minimal element. Let C=(
$\mathcal{B}^{sg}$
has a minimal element. Let C=(
![]() $p_1\succ p_2\succ \dots \succ p_t \succ \dots)$
be a descending chain of paths in
$p_1\succ p_2\succ \dots \succ p_t \succ \dots)$
be a descending chain of paths in
![]() $\mathcal{B}^{sg}$
. By construction of
$\mathcal{B}^{sg}$
. By construction of
![]() $kQ^{sg}$
, each path
$kQ^{sg}$
, each path
![]() $p_r$
is a sequence of arrows of the form
$p_r$
is a sequence of arrows of the form
![]() $(i_{r_1}, \alpha_{r_1},j_{r_1})\dots (i_{r_l}, \alpha_{r_l},j_{r_l})$
such that
$(i_{r_1}, \alpha_{r_1},j_{r_1})\dots (i_{r_l}, \alpha_{r_l},j_{r_l})$
such that
![]() $\alpha_{r_1}\dots \alpha_{r_l}$
is a path
$\alpha_{r_1}\dots \alpha_{r_l}$
is a path
![]() $\widehat{p_r}$
in Q and
$\widehat{p_r}$
in Q and
![]() $C'=(\widehat{p_1}\succ_Q \widehat{p_2}\succ_Q \dots \succ_Q \widehat{p_t} \succ_Q \dots)$
is a descending chain of elements in
$C'=(\widehat{p_1}\succ_Q \widehat{p_2}\succ_Q \dots \succ_Q \widehat{p_t} \succ_Q \dots)$
is a descending chain of elements in
![]() $\mathcal{B}$
. Since
$\mathcal{B}$
. Since
![]() $\succ_Q$
is an admissible order on
$\succ_Q$
is an admissible order on
![]() $\mathcal{B}$
, the chain C
$\mathcal{B}$
, the chain C
![]() $^{\prime}$
has a minimal element
$^{\prime}$
has a minimal element
![]() $\widehat{p}_r$
, for some
$\widehat{p}_r$
, for some
![]() $r\in\mathbb N$
, such that
$r\in\mathbb N$
, such that
![]() $\widehat{p}_r=\widehat{p}_{r+m}$
for all
$\widehat{p}_r=\widehat{p}_{r+m}$
for all
![]() $m\in\mathbb N$
, therefore there exists some
$m\in\mathbb N$
, therefore there exists some
![]() $r' \in \mathbb N$
such that
$r' \in \mathbb N$
such that
![]() $p_{r^{\prime}}=p_{r^{\prime}+m}$
for all
$p_{r^{\prime}}=p_{r^{\prime}+m}$
for all
![]() $m\in\mathbb N$
.
$m\in\mathbb N$
.
Thus, the order
![]() $\succ$
on the basis of paths
$\succ$
on the basis of paths
![]() $\mathcal{B}^{sg}$
of
$\mathcal{B}^{sg}$
of
![]() $KQ^{sg}$
is admissible.
$KQ^{sg}$
is admissible.
Proposition 4.6 Let A be a locally skew-gentle algebra, then A is strong Koszul.
Proof. Let A be a locally skew-gentle algebra,
![]() $\Lambda=KQ/I$
be the locally gentle algebra obtained from A by deleting special loops. Consider the admissible presentation of A, namely
$\Lambda=KQ/I$
be the locally gentle algebra obtained from A by deleting special loops. Consider the admissible presentation of A, namely
![]() $A^{sg}=KQ^{sg}/I^{sg}$
. By [Reference Green and Huang19, Theorem 3] it is enough to prove that there exists a quadratic Gröbner basis for the ideal
$A^{sg}=KQ^{sg}/I^{sg}$
. By [Reference Green and Huang19, Theorem 3] it is enough to prove that there exists a quadratic Gröbner basis for the ideal
![]() $I^{sg}$
. Let
$I^{sg}$
. Let
![]() $\succ_Q$
be an admissible order on
$\succ_Q$
be an admissible order on
![]() $\mathcal{B}$
the basis of path of KQ, for example, and more precisely let
$\mathcal{B}$
the basis of path of KQ, for example, and more precisely let
![]() $\succ_Q$
be a paths length lexicographical order. By Lemma 4.5, there exists an admissible order
$\succ_Q$
be a paths length lexicographical order. By Lemma 4.5, there exists an admissible order
![]() $\succ$
on
$\succ$
on
![]() $\mathcal{B}^{sg}$
, the basis of paths of
$\mathcal{B}^{sg}$
, the basis of paths of
![]() $KQ^{sg}$
such that:
$KQ^{sg}$
such that:
-
(1) if
 $\alpha\neq \beta$
then
$\alpha\neq \beta$
then
 $(i, \alpha, j)\succ (i', \beta, j')$
if and only if
$(i, \alpha, j)\succ (i', \beta, j')$
if and only if
 $\alpha \succ_Q \beta$
;
$\alpha \succ_Q \beta$
; -
(2) the order on the set of arrows of
 $Q^{sg}$
associated with an arrow
$Q^{sg}$
associated with an arrow
 $\alpha$
in Q ending or starting in a special vertex is given as follows: If i and j are special vertices, then
$\alpha$
in Q ending or starting in a special vertex is given as follows: If i and j are special vertices, then
 $(i^+, \alpha, j^+) \succ (i^-,\alpha, j^-) \succ (i^+, \alpha, j^-) \succ (i^-, \alpha, j^+)$
. If i is a special vertex and
$(i^+, \alpha, j^+) \succ (i^-,\alpha, j^-) \succ (i^+, \alpha, j^-) \succ (i^-, \alpha, j^+)$
. If i is a special vertex and
 $t(\alpha)$
is not special (resp. i not special and j special), then
$t(\alpha)$
is not special (resp. i not special and j special), then
 $(i^+, \alpha, j) \succ (i^-,\alpha, j)$
(resp.
$(i^+, \alpha, j) \succ (i^-,\alpha, j)$
(resp.
 $(i, \alpha, j^+) \succ (i,\alpha, j^-)$
).
$(i, \alpha, j^+) \succ (i,\alpha, j^-)$
).
We claim that the set
 \begin{equation*}\mathcal G= \left\{\sum_{j\in Q_0^{sg}(s(\beta))}\lambda_j(i,\alpha, j)(j,\beta, k)\mid \alpha\beta\in I, i\in Q_0^{sg}(s(\alpha)), k\in Q_0^{sg}(t(\beta))\right\},\end{equation*}
\begin{equation*}\mathcal G= \left\{\sum_{j\in Q_0^{sg}(s(\beta))}\lambda_j(i,\alpha, j)(j,\beta, k)\mid \alpha\beta\in I, i\in Q_0^{sg}(s(\alpha)), k\in Q_0^{sg}(t(\beta))\right\},\end{equation*}
where
![]() $\lambda_j=-1$
if
$\lambda_j=-1$
if
![]() $j=l^-$
for some
$j=l^-$
for some
![]() $l\in Q_0$
, and
$l\in Q_0$
, and
![]() $\lambda_j=1$
otherwise, is Gröbner basis for
$\lambda_j=1$
otherwise, is Gröbner basis for
![]() $I^{sg}$
. By [Reference Green, Hille and Schroll22, Theorem 2.13], it is enough to show that every overlap relation of any two elements of
$I^{sg}$
. By [Reference Green, Hille and Schroll22, Theorem 2.13], it is enough to show that every overlap relation of any two elements of
![]() $\mathcal{G}$
completely reduces to 0 by
$\mathcal{G}$
completely reduces to 0 by
![]() $\mathcal{G}$
. It follows from the definition of
$\mathcal{G}$
. It follows from the definition of
![]() $A^{sg}$
that any element in
$A^{sg}$
that any element in
![]() $\mathcal{G}$
is a linear combination with at most two summands. Let
$\mathcal{G}$
is a linear combination with at most two summands. Let
![]() $x=\lambda_1(i, \alpha, j)(j, \beta, k)+ \lambda_2(i, \alpha, j')(j', \beta,k)$
and
$x=\lambda_1(i, \alpha, j)(j, \beta, k)+ \lambda_2(i, \alpha, j')(j', \beta,k)$
and
![]() $y=\mu_1(j,\beta,k)(k, \gamma, l) +\mu_2(j,\beta, k')(k', \gamma, l)$
be elements in
$y=\mu_1(j,\beta,k)(k, \gamma, l) +\mu_2(j,\beta, k')(k', \gamma, l)$
be elements in
![]() $\mathcal G$
and
$\mathcal G$
and
![]() $n, m\in \mathcal B$
such that
$n, m\in \mathcal B$
such that
![]() $\mathbf o(x, y, m,n)$
is a overlap relation. Observe that in this case, by the definition of the overlap relation, n and m are arrows. It is easy to check that if x or y are monomial relations, then
$\mathbf o(x, y, m,n)$
is a overlap relation. Observe that in this case, by the definition of the overlap relation, n and m are arrows. It is easy to check that if x or y are monomial relations, then
![]() $\mathbf o(x, y, m,n)$
is also a monomial relation in
$\mathbf o(x, y, m,n)$
is also a monomial relation in
![]() $A^{sg}$
. Suppose that x and y are binomial relations, and suppose
$A^{sg}$
. Suppose that x and y are binomial relations, and suppose
![]() $t=\operatorname{tip}(x)=(i, \alpha, j)(j, \beta, k)$
and
$t=\operatorname{tip}(x)=(i, \alpha, j)(j, \beta, k)$
and
![]() $t'=\operatorname{tip}(y)=(j,\beta,k)(k, \gamma, l)$
, then the overlap relation is written as follows
$t'=\operatorname{tip}(y)=(j,\beta,k)(k, \gamma, l)$
, then the overlap relation is written as follows
where
![]() $n=(k, \gamma, l)$
and
$n=(k, \gamma, l)$
and
![]() $m=(i, \alpha, j)$
. Observe that by the definition of the relations in
$m=(i, \alpha, j)$
. Observe that by the definition of the relations in
![]() $I^{sg}$
and by definition of the admissible order
$I^{sg}$
and by definition of the admissible order
![]() $\succ$
, we have that
$\succ$
, we have that
![]() $(j,\beta,k)$
is either
$(j,\beta,k)$
is either
![]() $(s(\beta)^+, \beta, t(\beta)^+)$
or
$(s(\beta)^+, \beta, t(\beta)^+)$
or
![]() $(s(\beta)^{-}, \beta, t(\beta)^-)$
. Moreover, there is no element
$(s(\beta)^{-}, \beta, t(\beta)^-)$
. Moreover, there is no element
![]() $z\in \mathcal{G}$
such that
$z\in \mathcal{G}$
such that
![]() $\operatorname{tip}(z)$
is starting with
$\operatorname{tip}(z)$
is starting with
![]() $(j', \beta, k)$
or
$(j', \beta, k)$
or
![]() $(j, \beta, k')$
. Therefore, any simple reduction of
$(j, \beta, k')$
. Therefore, any simple reduction of
![]() $\mathbf{o}(x,y,n,m)$
replaces the second element
$\mathbf{o}(x,y,n,m)$
replaces the second element
![]() $(i, \alpha, j)(j,\beta, k')(k', \gamma, l)$
with:
$(i, \alpha, j)(j,\beta, k')(k', \gamma, l)$
with:
Finally, if there exist an element w in
![]() $\mathcal{G}$
such that
$\mathcal{G}$
such that
![]() $\operatorname{tip}(w)$
is starting with
$\operatorname{tip}(w)$
is starting with
![]() $(j', \beta, k')$
then we can reduce
$(j', \beta, k')$
then we can reduce
![]() $(i, \alpha, j')(j',\beta, k')(k', \gamma, l)$
as follows:
$(i, \alpha, j')(j',\beta, k')(k', \gamma, l)$
as follows:
which implies that the quadratic basis
![]() $\mathcal G$
is a Gröbner basis, and as a consequence, A is a Koszul algebra.
$\mathcal G$
is a Gröbner basis, and as a consequence, A is a Koszul algebra.
Before we state the last result of this section, we recall the definition of Koszul dual, see [Reference Martínez-Villa34] for details. The Koszul dual
![]() $A^!$
of a finite dimensional Koszul algebra A is by definition the algebra
$A^!$
of a finite dimensional Koszul algebra A is by definition the algebra
![]() $\operatorname{Ext}_A(A/ \operatorname{rad}(A), A/ \operatorname{rad}(A))^{op}$
, which is isomorphic to the quadratic dual of A. For the convenience of the reader, we briefly recall the construction of
$\operatorname{Ext}_A(A/ \operatorname{rad}(A), A/ \operatorname{rad}(A))^{op}$
, which is isomorphic to the quadratic dual of A. For the convenience of the reader, we briefly recall the construction of
![]() $A^!$
for algebras of the form
$A^!$
for algebras of the form
![]() $KQ/I$
. Let
$KQ/I$
. Let
![]() $V=KQ_2$
be the vector space generated by the paths of length two and
$V=KQ_2$
be the vector space generated by the paths of length two and
![]() $\{\gamma_1, \dots, \gamma_r\}$
be a basis of V. Denote by
$\{\gamma_1, \dots, \gamma_r\}$
be a basis of V. Denote by
![]() $V^{op}$
the vector space generated by paths of length two in
$V^{op}$
the vector space generated by paths of length two in
![]() $Q^{op}$
with dual basis
$Q^{op}$
with dual basis
![]() $\{\gamma_1^{op}, \dots, \gamma_n^{op}\}$
.
$\{\gamma_1^{op}, \dots, \gamma_n^{op}\}$
.
Following [Reference Martínez-Villa34], the orthogonal ideal
![]() $I_2^{\bot}$
is generated by
$I_2^{\bot}$
is generated by
where
![]() $\langle , \rangle{:}V \times V^{op}\to k $
is a bilinear form defined on bases elements as follows:
$\langle , \rangle{:}V \times V^{op}\to k $
is a bilinear form defined on bases elements as follows:
 \begin{equation*}\langle \gamma_i, \gamma_j^{op}\rangle=\begin{cases}0 & \text{\ if \ } \gamma_i\neq \gamma_j,\\[3pt] 1 & \text{\ otherwise. }\end{cases}\end{equation*}
\begin{equation*}\langle \gamma_i, \gamma_j^{op}\rangle=\begin{cases}0 & \text{\ if \ } \gamma_i\neq \gamma_j,\\[3pt] 1 & \text{\ otherwise. }\end{cases}\end{equation*}
Then, the Koszul dual
![]() $A^!$
of A is the path algebra
$A^!$
of A is the path algebra
![]() $KQ^{op}/ I_{2}^{\bot}$
.
$KQ^{op}/ I_{2}^{\bot}$
.
Proposition 4.7 Let
![]() $A=KQ^{sg}/I^{sg}$
be the admissible presentation of a skew-gentle algebra and
$A=KQ^{sg}/I^{sg}$
be the admissible presentation of a skew-gentle algebra and
![]() $A^!$
its Koszul dual. Then the admissible ideal
$A^!$
its Koszul dual. Then the admissible ideal
![]() $I_2^{\bot}$
of
$I_2^{\bot}$
of
![]() $A^{!}$
is generated by:
$A^{!}$
is generated by:
-
• paths of length two which are not a summand of a minimal generator of
 $I^{sg}$
$I^{sg}$
-
• commutativity relations in
 $I^{sg}$
.
$I^{sg}$
.
Proof. Let W be the set of generators of the ideal
![]() $I^{sg}$
, namely
$I^{sg}$
, namely
 \begin{equation*}W= \left\{\sum_{j\in Q_0^{sg}(s(\beta))}\lambda_j(i,\alpha, j)(j,\beta, k)\mid \alpha\beta\in I, i\in Q_0^{sg}(s(\alpha)), k\in Q_0^{sg}(t(\beta))\right\},\end{equation*}
\begin{equation*}W= \left\{\sum_{j\in Q_0^{sg}(s(\beta))}\lambda_j(i,\alpha, j)(j,\beta, k)\mid \alpha\beta\in I, i\in Q_0^{sg}(s(\alpha)), k\in Q_0^{sg}(t(\beta))\right\},\end{equation*}
where
![]() $\lambda_j=-1$
if
$\lambda_j=-1$
if
![]() $j=l^{-}$
for some
$j=l^{-}$
for some
![]() $l\in Q_0$
, and
$l\in Q_0$
, and
![]() $\lambda_j=1$
otherwise.
$\lambda_j=1$
otherwise.
Then, the orthogonal ideal
![]() $I_2^{\bot}$
is generated by
$I_2^{\bot}$
is generated by
where
![]() $\langle , \rangle:V \times V^{op}\to k $
is a bilinear form defined on bases elements as follows:
$\langle , \rangle:V \times V^{op}\to k $
is a bilinear form defined on bases elements as follows:
 \begin{equation*}\langle \gamma_i, \gamma_j^{op}\rangle=\begin{cases}0 & \text{\ if \ } \gamma_i\neq \gamma_j,\\ \\[-7pt]1 & \text{\ otherwise. }\end{cases}\end{equation*}
\begin{equation*}\langle \gamma_i, \gamma_j^{op}\rangle=\begin{cases}0 & \text{\ if \ } \gamma_i\neq \gamma_j,\\ \\[-7pt]1 & \text{\ otherwise. }\end{cases}\end{equation*}
By definition of B, any path of length two which is not a summand of a minimal generator of
![]() $I^{sg}$
is an element of B. Let x be uniform element in B which is by definition of V a linear combination of at most two paths. To fix notation, let
$I^{sg}$
is an element of B. Let x be uniform element in B which is by definition of V a linear combination of at most two paths. To fix notation, let
![]() $x=\lambda_1\rho_1+\lambda_2\rho_2$
be a linear combination of two paths
$x=\lambda_1\rho_1+\lambda_2\rho_2$
be a linear combination of two paths
![]() $\rho_1$
and
$\rho_1$
and
![]() $\rho_2$
with the same source and target with
$\rho_2$
with the same source and target with
![]() $\lambda_1, \lambda_2 \in K^*$
.
$\lambda_1, \lambda_2 \in K^*$
.
Suppose for contradiction that
![]() $\rho_1$
is a monomial relation. Then
$\rho_1$
is a monomial relation. Then
![]() $\langle \rho_1, x\rangle=0$
implies that
$\langle \rho_1, x\rangle=0$
implies that
![]() $\lambda_1=0$
which is a contradiction. Therefore without loss of generality, we have
$\lambda_1=0$
which is a contradiction. Therefore without loss of generality, we have
![]() $\rho_1 - \rho_2 \in V$
and
$\rho_1 - \rho_2 \in V$
and
![]() $\langle \rho_1-\rho_2, x\rangle=0$
implies that
$\langle \rho_1-\rho_2, x\rangle=0$
implies that
![]() $\lambda_1=\lambda_2$
that is
$\lambda_1=\lambda_2$
that is
![]() $x = \rho_1+\rho_2$
.
$x = \rho_1+\rho_2$
.
Using the isomorphism
![]() $\varphi{:}KQ^{sg} \to KQ^{sg}$
defined by
$\varphi{:}KQ^{sg} \to KQ^{sg}$
defined by
 \begin{equation*}\varphi((i, \alpha, j))=\begin{cases}-(i, \alpha, j) & \text{ if } i=s(\alpha)^+ \text{ and } j=t(\alpha)^+ \text{ or } i=s(\alpha)^- \text{ and } j=t(\alpha)^-;\\ \\[-7pt](i, \alpha, j) & \text{ otherwise. }\end{cases}\end{equation*}
\begin{equation*}\varphi((i, \alpha, j))=\begin{cases}-(i, \alpha, j) & \text{ if } i=s(\alpha)^+ \text{ and } j=t(\alpha)^+ \text{ or } i=s(\alpha)^- \text{ and } j=t(\alpha)^-;\\ \\[-7pt](i, \alpha, j) & \text{ otherwise. }\end{cases}\end{equation*}
the result follows.
The following Theorem shows how to compute the generalised ribbon graph of the Koszul dual of a skew-gentle algebra.
Theorem-Definition 4.8 Let A be a skew-gentle algebra, and let
![]() $(S,M,\mathcal{O}, G_A)$
be the orbifold dissection of A. Denote by
$(S,M,\mathcal{O}, G_A)$
be the orbifold dissection of A. Denote by
![]() $G_A^*$
the graph embedded in a surface obtained from
$G_A^*$
the graph embedded in a surface obtained from
![]() $(S, M, \mathcal{O})$
as follows.
$(S, M, \mathcal{O})$
as follows.
-
• In each boundary edge of the dissection
 $G_A$
, there is exactly one vertex of
$G_A$
, there is exactly one vertex of
 $G_A^*$
. In addition, any unmarked boundary in
$G_A^*$
. In addition, any unmarked boundary in
 $(S,M,\mathcal{O})$
is replaced by a vertex of
$(S,M,\mathcal{O})$
is replaced by a vertex of
 $G_A^*$
.
$G_A^*$
. -
• Any orbifold point in
 $G_A$
is also an orbifold point in
$G_A$
is also an orbifold point in
 $G_A^*$
.
$G_A^*$
.
Then for every non-special edge v of
![]() $G_A,$
there is a unique edge in
$G_A,$
there is a unique edge in
![]() $G_A^*$
crossing v exactly once. Every special edge of
$G_A^*$
crossing v exactly once. Every special edge of
![]() $G_A$
corresponds to an edge of
$G_A$
corresponds to an edge of
![]() $G_A^*$
connecting the orbifold point with the unique vertex of
$G_A^*$
connecting the orbifold point with the unique vertex of
![]() $G_A^*$
such that the resulting edge does not cross any edge of
$G_A^*$
such that the resulting edge does not cross any edge of
![]() $G_A$
. We call these edges of
$G_A$
. We call these edges of
![]() $G_A^*$
special edges.
$G_A^*$
special edges.
Then
![]() $G_A^*$
is the graph of the Koszul dual
$G_A^*$
is the graph of the Koszul dual
![]() $A^{!}$
.
$A^{!}$
.
Proof. This follows directly from the construction of
![]() $G_A^*$
and Proposition 4.7.
$G_A^*$
and Proposition 4.7.
In Figure 4, we can see the dual graphs of the generalised ribbon graphs from Example 3.5.

Figure 4. Dissections for the skew-gentle algebra and its Koszul dual associated with
![]() $\mathbb{D}_5$
on the left and
$\mathbb{D}_5$
on the left and
![]() $A_2$
on the right from Example 2.4
$A_2$
on the right from Example 2.4
Example 4.9 Let Q be the quiver
and
![]() $\mathcal{R}_1=\{\alpha_1\alpha_2,\alpha_2\alpha_3,\alpha_3\alpha_1,\varepsilon^2-\varepsilon\}$
and
$\mathcal{R}_1=\{\alpha_1\alpha_2,\alpha_2\alpha_3,\alpha_3\alpha_1,\varepsilon^2-\varepsilon\}$
and
![]() $\mathcal{R}_2=\{\alpha_1\alpha_2,\alpha_2\alpha_3, \varepsilon^2-\varepsilon\}$
. The algebras
$\mathcal{R}_2=\{\alpha_1\alpha_2,\alpha_2\alpha_3, \varepsilon^2-\varepsilon\}$
. The algebras
![]() $A_1=KQ/\langle\mathcal{R}_1\rangle$
and
$A_1=KQ/\langle\mathcal{R}_1\rangle$
and
![]() $A_2=KQ/\langle \mathcal{R}_2\rangle$
are skew-gentle. Orbifold dissections and their duals are depicted in Figure 5.
$A_2=KQ/\langle \mathcal{R}_2\rangle$
are skew-gentle. Orbifold dissections and their duals are depicted in Figure 5.

Figure 5. Orbifold dissection and dual graph for
![]() $A_1$
and
$A_1$
and
![]() $A_2$
$A_2$
5. Graded curves in an orbifold dissection
In this section, we define graded curves in an orbifold with marked points. We begin by recalling from [Reference Chas and Gadgil13] the notion of homotopy in an orbifold based on what is called skein relations in that paper.
Let A be a skew-gentle algebra and O be the associated orbifold. We recall the notion of O-free homotopy from [Reference Chas and Gadgil13].
Definition 5.1 Two oriented closed curves
![]() $\gamma$
and
$\gamma$
and
![]() $\gamma'$
in O are O-homotopic if they are related by a finite number of moves given by either a homotopy in the complement of the orbifold points or are related by moves taking place in a disk D containing exactly one orbifold point
$\gamma'$
in O are O-homotopic if they are related by a finite number of moves given by either a homotopy in the complement of the orbifold points or are related by moves taking place in a disk D containing exactly one orbifold point
![]() $o_x$
as in Figure 6. That is, a segment of a curve with no self-intersection in D and passing through
$o_x$
as in Figure 6. That is, a segment of a curve with no self-intersection in D and passing through
![]() $o_x$
is O-homotopic relative to its endpoints to a segment spiralling around
$o_x$
is O-homotopic relative to its endpoints to a segment spiralling around
![]() $\omega$
in either direction exactly once as in Figure 6.
$\omega$
in either direction exactly once as in Figure 6.
As a consequence of Definition 5.1 the curves in Figure 7 are O-homotopic in O.
Definition 5.2 Let
![]() $O=(S,M,\mathcal{O})$
be an orbifold with set
$O=(S,M,\mathcal{O})$
be an orbifold with set
![]() $\mathcal{O}$
of orbifold points of order 2 with a finite set M of marked points in the boundary component of S or in the interior of S. Let x, y be marked points.
$\mathcal{O}$
of orbifold points of order 2 with a finite set M of marked points in the boundary component of S or in the interior of S. Let x, y be marked points.
-
(1) If x and y are marked points in the boundary of S, a finite arc (or simply an arc)
 $\gamma$
from x to y is an O-homotopy class, relative to endpoints, of non-contractible curves
$\gamma$
from x to y is an O-homotopy class, relative to endpoints, of non-contractible curves
 $\gamma$
from x to y in O.
$\gamma$
from x to y in O. -
(2) A closed curve
 $\gamma$
is a free O-homotopy class of non-contractible closed curves
$\gamma$
is a free O-homotopy class of non-contractible closed curves
 $\gamma$
not passing through any orbifold points.
$\gamma$
not passing through any orbifold points. -
(3) An infinite arc is an O-homotopy class
 $\gamma$
associated with rays, that is a continuous maps
$\gamma$
associated with rays, that is a continuous maps
 $r{:}(0,1]\to O$
(or
$r{:}(0,1]\to O$
(or
 $r{:}[0,1) \to O$
) or
$r{:}[0,1) \to O$
) or
 $l{:}(0,1) \to O$
respectively, that wrap around an unmarked boundary component in a clockwise way, asymptotically approaching this boundary.
$l{:}(0,1) \to O$
respectively, that wrap around an unmarked boundary component in a clockwise way, asymptotically approaching this boundary.Recall that two rays
 $r{:} (0, 1] \to O$
and
$r{:} (0, 1] \to O$
and
 $r'{:} (0, 1] \to O$
are O-homotopic if they wrap infinitely many times around the same unmarked boundary component B, their endpoints coinciding in the marked point x in the boundary, and if for every closed neighbourhood N of B the induced maps
$r'{:} (0, 1] \to O$
are O-homotopic if they wrap infinitely many times around the same unmarked boundary component B, their endpoints coinciding in the marked point x in the boundary, and if for every closed neighbourhood N of B the induced maps
 $r,r'{:} \left[0,1\right] \to O \setminus N$
are O-homotopic relative to their endpoints. Similarly, we say two lines
$r,r'{:} \left[0,1\right] \to O \setminus N$
are O-homotopic relative to their endpoints. Similarly, we say two lines
 $l{:} (0,1)\to O$
and
$l{:} (0,1)\to O$
and
 $l'{:} (0, 1) \to O$
are equivalent if they wrap infinitely many times around the same unmarked boundary components B and B
$l'{:} (0, 1) \to O$
are equivalent if they wrap infinitely many times around the same unmarked boundary components B and B
 $^{\prime}$
on either end and if for every closed neighbourhood N of B and N
$^{\prime}$
on either end and if for every closed neighbourhood N of B and N
 $^{\prime}$
of B
$^{\prime}$
of B
 $^{\prime}$
the induced maps
$^{\prime}$
the induced maps
 $l, l'{:} [0, 1] \to O \setminus (N \cup N')$
are O-homotopic relative to their endpoints.
$l, l'{:} [0, 1] \to O \setminus (N \cup N')$
are O-homotopic relative to their endpoints.
Our main result requires a notion of grading on arcs and closed curves. This grading depends on the dual graph
![]() $G^*_A$
of a skew-gentle algebra A. Therefore before giving the definition, we will need some results on the geometry of the graph
$G^*_A$
of a skew-gentle algebra A. Therefore before giving the definition, we will need some results on the geometry of the graph
![]() $G^*_A$
. Moreover, since every unmarked boundary in a orbifold dissection
$G^*_A$
. Moreover, since every unmarked boundary in a orbifold dissection
![]() $(S,M, \mathcal{O}, G)$
of A is replaced by a vertex of
$(S,M, \mathcal{O}, G)$
of A is replaced by a vertex of
![]() $G^*$
, we will view unmarked boundary components as marked points in the interior. In particular, it will be useful to think of infinite arcs wrapping around a boundary component as infinite arcs wrapping around a marked points in the interior. We note that in our model, we only consider infinite arcs as in Definition 5.2(3), that is only those infinite arcs that wrap around an unmarked boundary component (i.e. a marked point in the interior of the surface) in a clockwise way.
$G^*$
, we will view unmarked boundary components as marked points in the interior. In particular, it will be useful to think of infinite arcs wrapping around a boundary component as infinite arcs wrapping around a marked points in the interior. We note that in our model, we only consider infinite arcs as in Definition 5.2(3), that is only those infinite arcs that wrap around an unmarked boundary component (i.e. a marked point in the interior of the surface) in a clockwise way.

Figure 6. Moves in a disk containing exactly one orbifold point.

Figure 7. O-homotopic curves in a disk containing one orbifold point.
Lemma 5.3 Let
![]() $A=KQ/I$
be a skew-gentle algebra with orbifold
$A=KQ/I$
be a skew-gentle algebra with orbifold
![]() $O_A = (S,M,\mathcal{O})$
with set of marked points M and embedded generalised ribbon graph
$O_A = (S,M,\mathcal{O})$
with set of marked points M and embedded generalised ribbon graph
![]() $G_A$
. Then the dual graph
$G_A$
. Then the dual graph
![]() $G^*_A$
subdivides
$G^*_A$
subdivides
![]() $O_A$
into polygons and degenerate polygons, where the edges of each such polygon are edges of
$O_A$
into polygons and degenerate polygons, where the edges of each such polygon are edges of
![]() $G^*_A$
and exactly one boundary segment containing exactly one marked point of M.
$G^*_A$
and exactly one boundary segment containing exactly one marked point of M.
Proof. Let
![]() $\Lambda$
be the gentle algebra obtained from A by deleting all special loops in Q and let
$\Lambda$
be the gentle algebra obtained from A by deleting all special loops in Q and let
![]() $(S, M_\Lambda, G_\Lambda)$
be surface dissection associated with
$(S, M_\Lambda, G_\Lambda)$
be surface dissection associated with
![]() $\Lambda$
. By [Reference Opper, Plamondon and Schroll35, Lemma 2.6] and Remark 3.2, the dual graph
$\Lambda$
. By [Reference Opper, Plamondon and Schroll35, Lemma 2.6] and Remark 3.2, the dual graph
![]() $G^*_{\Lambda}$
of
$G^*_{\Lambda}$
of
![]() $\Lambda$
subdivides
$\Lambda$
subdivides
![]() $S_{\Lambda}$
into polygons and degenerate polygons, where the edges of each such polygon are edges of
$S_{\Lambda}$
into polygons and degenerate polygons, where the edges of each such polygon are edges of
![]() $G^*_\Lambda$
and exactly one boundary segment containing exactly one marked point of
$G^*_\Lambda$
and exactly one boundary segment containing exactly one marked point of
![]() $M_\Lambda$
.
$M_\Lambda$
.
It is enough to observe that after a local replacement of a special edge
![]() $\gamma$
in
$\gamma$
in
![]() $G_{\Lambda}$
, the unique edge
$G_{\Lambda}$
, the unique edge
![]() $\gamma^*$
of
$\gamma^*$
of
![]() $G^*_\Lambda$
crossing
$G^*_\Lambda$
crossing
![]() $\gamma$
corresponds to a special edge in
$\gamma$
corresponds to a special edge in
![]() $G^*$
. By definition
$G^*$
. By definition
![]() $\gamma^*$
is connected to an orbifold point
$\gamma^*$
is connected to an orbifold point
![]() $o_x$
. Let P and P
$o_x$
. Let P and P
![]() $^{\prime}$
be the polygons in of
$^{\prime}$
be the polygons in of
![]() $G^*_\Lambda$
in S sharing the common edge
$G^*_\Lambda$
in S sharing the common edge
![]() $\gamma^*$
. As a consequence of the local replacement, P and P
$\gamma^*$
. As a consequence of the local replacement, P and P
![]() $^{\prime}$
correspond to a single degenerate polygon in S containing
$^{\prime}$
correspond to a single degenerate polygon in S containing
![]() $o_x$
, see Figure 8. The result follows.
$o_x$
, see Figure 8. The result follows.

Figure 8. Degenerate polygon after the local replacement of a special edge in
![]() $G_\Lambda$
and
$G_\Lambda$
and
![]() $G^*_{\Lambda}$
.
$G^*_{\Lambda}$
.

Figure 9. O-homotopic curves.
By the Lemma 5.3,
![]() $G^*_A$
induces a dissection of
$G^*_A$
induces a dissection of
![]() $O_A$
. Furthermore, the generalised polygons of
$O_A$
. Furthermore, the generalised polygons of
![]() $G^*_A$
are in bijection with vertices of
$G^*_A$
are in bijection with vertices of
![]() $G_A$
.
$G_A$
.
Remark 5.4 (1) We assume that any finite collection of curves is in
![]() ${minimal position}$
, that is, the number of intersections of each pair of (not necessarily distinct) curves in this set is minimal.
${minimal position}$
, that is, the number of intersections of each pair of (not necessarily distinct) curves in this set is minimal.
(2) If
![]() $\gamma$
is an arc or closed curve in an orbifold dissection
$\gamma$
is an arc or closed curve in an orbifold dissection
![]() $(S,M,\mathcal O, G),$
we always assume that
$(S,M,\mathcal O, G),$
we always assume that
![]() $\gamma$
crosses every edge of G transversely.
$\gamma$
crosses every edge of G transversely.
(3) In Figure 9, we give examples of O-homotopic curves. In each case, the first curve represents the chosen representative in its O-homotopic class which we will usually be working with.
Definition 5.5 Given a skew-gentle algebra A and the associated graph
![]() $G_A$
with vertex set M, with dual graph
$G_A$
with vertex set M, with dual graph
![]() $G^*_A$
and associated orbifold
$G^*_A$
and associated orbifold
![]() $O = (S,M, \mathcal{O})$
, we call the tuple
$O = (S,M, \mathcal{O})$
, we call the tuple
![]() $(S, M, \mathcal{O}, G^*_A)$
the orbifold dissection associated with A.
$(S, M, \mathcal{O}, G^*_A)$
the orbifold dissection associated with A.
We note that if
![]() $(S, M,\mathcal{O}, G^*)$
is an orbifold dissection and if
$(S, M,\mathcal{O}, G^*)$
is an orbifold dissection and if
![]() $\gamma$
is a possibly infinite arc or a closed curve in O, then
$\gamma$
is a possibly infinite arc or a closed curve in O, then
![]() $\gamma$
is completely determined by the possibly infinite sequence of edges of
$\gamma$
is completely determined by the possibly infinite sequence of edges of
![]() $G^*$
which it crosses. If
$G^*$
which it crosses. If
![]() $\gamma$
is a closed curve, then this sequence is determined up to cyclic permutation.
$\gamma$
is a closed curve, then this sequence is determined up to cyclic permutation.
Definition 5.6 Let
![]() $\gamma$
be an arc or a closed curve in an orbifold dissection
$\gamma$
be an arc or a closed curve in an orbifold dissection
![]() $(S,M,\mathcal{O}, G)$
and let
$(S,M,\mathcal{O}, G)$
and let
![]() $\left(x_i\right)$
be the ordered multiset of edges of the dual graph
$\left(x_i\right)$
be the ordered multiset of edges of the dual graph
![]() $G^*$
of G crossed successively by
$G^*$
of G crossed successively by
![]() $\gamma$
.
$\gamma$
.
Let
![]() $\left[x_{i}, x_{i+1}\right]$
be the oriented segment going from
$\left[x_{i}, x_{i+1}\right]$
be the oriented segment going from
![]() $x_i$
to
$x_i$
to
![]() $x_{i+1}$
. Then, both
$x_{i+1}$
. Then, both
![]() $x_i$
and
$x_i$
and
![]() $x_{i+1}$
are edges of the same (degenerate) polygon P which contains exactly one marked point
$x_{i+1}$
are edges of the same (degenerate) polygon P which contains exactly one marked point
![]() $m \in M$
. A grading on
$m \in M$
. A grading on
![]() $\gamma$
is a function
$\gamma$
is a function
![]() $f:\left(x_i\right) \to \mathbb Z$
satisfying the following conditions.
$f:\left(x_i\right) \to \mathbb Z$
satisfying the following conditions.
 \begin{equation*}f(x_{i+1})=\begin{cases}f(x_i)+1 & \textrm{if m is to the left of $\left[x_{i}, x_{i+1}\right]$ in P;} \\ \\[-7pt] f(x_i)-1 & \textrm{if m is to the right of $\left[x_{i}, x_{i+1}\right]$ in P.}\end{cases}\end{equation*}
\begin{equation*}f(x_{i+1})=\begin{cases}f(x_i)+1 & \textrm{if m is to the left of $\left[x_{i}, x_{i+1}\right]$ in P;} \\ \\[-7pt] f(x_i)-1 & \textrm{if m is to the right of $\left[x_{i}, x_{i+1}\right]$ in P.}\end{cases}\end{equation*}
If
![]() $\gamma$
is an (infinite) arc, we say that
$\gamma$
is an (infinite) arc, we say that
![]() $(\gamma, f)$
is an (infinite) graded arc on
$(\gamma, f)$
is an (infinite) graded arc on
![]() $S_{A}$
. If
$S_{A}$
. If
![]() $\gamma$
is a closed curve successively crossing the edges
$\gamma$
is a closed curve successively crossing the edges
![]() $x_1, \dots, x_n$
of
$x_1, \dots, x_n$
of
![]() $G^*$
, we say that
$G^*$
, we say that
![]() $(\gamma, f)$
is a graded closed curve if the grading f is such that
$(\gamma, f)$
is a graded closed curve if the grading f is such that
![]() $f(x_1) = f(x_n)$
.
$f(x_1) = f(x_n)$
.
6. Indecomposable objects in the derived category of a skew-gentle algebra
In this section, given a skew-gentle algebra A, we show that the geometric model constructed in Section 3 is a model for the bounded derived category
![]() $D^b(A)$
. More precisely, using the equivalence
$D^b(A)$
. More precisely, using the equivalence
![]() $D^b(A)$
and
$D^b(A)$
and
![]() $K^{-,b}(proj-A)$
, we establish a one to one correspondence between the homotopy strings and bands encoding the indecomposable objects in
$K^{-,b}(proj-A)$
, we establish a one to one correspondence between the homotopy strings and bands encoding the indecomposable objects in
![]() $K^{-,b}(proj-A)$
and graded arcs and curves in the orbifold associated with A.
$K^{-,b}(proj-A)$
and graded arcs and curves in the orbifold associated with A.
6.1 Homotopy strings and bands
We begin by briefly recalling the definition of homotopy strings and bands from [Reference Bekkert, Marcos and Merklen5]. Throughout this section, let A be a skew-gentle algebra and let
![]() $\Lambda=KQ/I$
be the associated gentle algebra obtained from A by deleting all special loops.
$\Lambda=KQ/I$
be the associated gentle algebra obtained from A by deleting all special loops.
The definition of homotopy strings and bands for skew-gentle algebras is based on another gentle algebra
![]() $A_+$
underlying A in the following way. Let B a minimal set of relations of
$A_+$
underlying A in the following way. Let B a minimal set of relations of
![]() $\Lambda=KQ/I$
and set
$\Lambda=KQ/I$
and set
![]() $J = \langle B\setminus \{\alpha\beta\mid \alpha\beta\in I, t(\alpha)\in Sp\} \rangle$
. Then by [Reference Bekkert, Marcos and Merklen5]
$J = \langle B\setminus \{\alpha\beta\mid \alpha\beta\in I, t(\alpha)\in Sp\} \rangle$
. Then by [Reference Bekkert, Marcos and Merklen5]
![]() $A_+= KQ/ J$
is a gentle algebra.
$A_+= KQ/ J$
is a gentle algebra.
For every arrow
![]() $\alpha \in Q_1$
, we define a formal inverse arrow
$\alpha \in Q_1$
, we define a formal inverse arrow
![]() $\overline{\alpha}$
where
$\overline{\alpha}$
where
![]() $s(\overline{\alpha}) = t(\alpha)$
and
$s(\overline{\alpha}) = t(\alpha)$
and
![]() $t(\overline{\alpha}) = s(\alpha)$
. For each path
$t(\overline{\alpha}) = s(\alpha)$
. For each path
![]() $w=\alpha_1\dots\alpha_k$
we define
$w=\alpha_1\dots\alpha_k$
we define
![]() $\overline{(\alpha_1\dots \alpha_k)}=\overline{\alpha_k}\dots \overline{\alpha_1}$
,
$\overline{(\alpha_1\dots \alpha_k)}=\overline{\alpha_k}\dots \overline{\alpha_1}$
,
![]() $s(\overline{w})=e(w)$
and
$s(\overline{w})=e(w)$
and
![]() $t(\overline{w})=s(w)$
. A walk w is sequence
$t(\overline{w})=s(w)$
. A walk w is sequence
![]() $w_1 \dots w_n$
where
$w_1 \dots w_n$
where
![]() $w_i$
is either an arrow or an inverse arrow such that
$w_i$
is either an arrow or an inverse arrow such that
![]() $s(w_{k+1})=e(w_k)$
.
$s(w_{k+1})=e(w_k)$
.
A string is a walk
![]() $w=w_1\dots w_n$
such that
$w=w_1\dots w_n$
such that
![]() $w_{k+1}\neq \overline{w_k}$
for
$w_{k+1}\neq \overline{w_k}$
for
![]() $1\leq k <n$
and such that no substring w
$1\leq k <n$
and such that no substring w
![]() $^{\prime}$
of w or its inverse
$^{\prime}$
of w or its inverse
![]() $\overline{w'}$
is in J. For every
$\overline{w'}$
is in J. For every
![]() $i\in Q_0$
, we denote by
$i\in Q_0$
, we denote by
![]() $e_i$
the string corresponding to the trivial walk at i.
$e_i$
the string corresponding to the trivial walk at i.
A string
![]() $w=w_1 \dots w_n$
is a direct (resp. inverse) homotopy letter if
$w=w_1 \dots w_n$
is a direct (resp. inverse) homotopy letter if
![]() $w_k$
is a direct (resp. inverse) arrow, for all
$w_k$
is a direct (resp. inverse) arrow, for all
![]() $1\leq k \leq n$
. A homotopy walk
$1\leq k \leq n$
. A homotopy walk
![]() $\sigma$
is a sequence
$\sigma$
is a sequence
![]() $\sigma_1\dots \sigma_r$
, where
$\sigma_1\dots \sigma_r$
, where
![]() $\sigma_k$
is a direct or inverse homotopy letter such that
$\sigma_k$
is a direct or inverse homotopy letter such that
![]() $s(\sigma_{k+1}) = t(\sigma_k)$
. We say that
$s(\sigma_{k+1}) = t(\sigma_k)$
. We say that
![]() $\sigma=\sigma_1\dots \sigma_r$
is a direct (resp. inverse) homotopy walk if
$\sigma=\sigma_1\dots \sigma_r$
is a direct (resp. inverse) homotopy walk if
![]() $\sigma_k$
is direct (resp. inverse), for all
$\sigma_k$
is direct (resp. inverse), for all
![]() $1\leq k \leq r$
. A walk
$1\leq k \leq r$
. A walk
![]() $\sigma$
(resp. a homotopy walk) is closed if
$\sigma$
(resp. a homotopy walk) is closed if
![]() $s(\sigma)=t(\sigma)$
. Given a (homotopy) walk
$s(\sigma)=t(\sigma)$
. Given a (homotopy) walk
![]() $\sigma=\sigma_1 \dots \sigma_r$
we denote by
$\sigma=\sigma_1 \dots \sigma_r$
we denote by
![]() $\sigma[m]=\sigma_{m+1} \dots \sigma_r\sigma_1 \dots \sigma_j$
its rotations where
$\sigma[m]=\sigma_{m+1} \dots \sigma_r\sigma_1 \dots \sigma_j$
its rotations where
![]() $m=1, \dots, r-1.$
$m=1, \dots, r-1.$
Definition 6.1 Let A be a skew-gentle algebra with
![]() $\Lambda=KQ/I$
be the associated gentle algebra obtained from A be deleting all special loops, and
$\Lambda=KQ/I$
be the associated gentle algebra obtained from A be deleting all special loops, and
![]() $A_+=KQ/J$
the associated gentle algebra as defined above.
$A_+=KQ/J$
the associated gentle algebra as defined above.
-
(1) A homotopy string is a homotopy walk
 $\sigma=\sigma_1\dots \sigma_r$
such that
$\sigma=\sigma_1\dots \sigma_r$
such that-
• if both
 $\sigma_i, \sigma_{i+1}$
are direct (resp. inverse) homotopy letters such that
$\sigma_i, \sigma_{i+1}$
are direct (resp. inverse) homotopy letters such that
 $\sigma_i$
(resp.
$\sigma_i$
(resp.
 $\overline{\sigma_{i+1}}$
) is not ending at a special vertex, then
$\overline{\sigma_{i+1}}$
) is not ending at a special vertex, then
 $\sigma_i \sigma_{i+1}\in J $
(resp.
$\sigma_i \sigma_{i+1}\in J $
(resp.
 $\overline{\sigma_i \sigma_{i+1}} \in J$
),
$\overline{\sigma_i \sigma_{i+1}} \in J$
), -
• if
 $\sigma_i, \overline{\sigma_{i+1}}$
(resp.
$\sigma_i, \overline{\sigma_{i+1}}$
(resp.
 $\overline{\sigma_{i}}, \sigma_{i+1}$
) are direct homotopy letters and
$\overline{\sigma_{i}}, \sigma_{i+1}$
) are direct homotopy letters and
 $\sigma_i$
(resp.
$\sigma_i$
(resp.
 $\overline{\sigma_{i}}$
) is not ending at a special vertex, then
$\overline{\sigma_{i}}$
) is not ending at a special vertex, then
 $\sigma_i \sigma_{i+1}$
is a string. A non-trivial homotopy string
$\sigma_i \sigma_{i+1}$
is a string. A non-trivial homotopy string
 $\sigma$
is
$\sigma$
is
 ${symmetric}$
if
${symmetric}$
if
 $\sigma=\overline{\sigma}$
and
$\sigma=\overline{\sigma}$
and
 ${asymmetric}$
otherwise.
${asymmetric}$
otherwise.
-
-
(2) A
 ${homotopy\ band}$
is a closed homotopy string
${homotopy\ band}$
is a closed homotopy string
 $\sigma=\sigma_1 \dots \sigma_{n}$
with an equal number of direct and inverse homotopy letters such that
$\sigma=\sigma_1 \dots \sigma_{n}$
with an equal number of direct and inverse homotopy letters such that
 $\sigma$
is not a proper power of some homotopy string
$\sigma$
is not a proper power of some homotopy string
 $\sigma '$
and such that every power of
$\sigma '$
and such that every power of
 $\sigma$
is a homotopy string.
$\sigma$
is a homotopy string.
A non-trivial homotopy band
![]() $\sigma$
is symmetric if
$\sigma$
is symmetric if
![]() $\sigma= \overline{\sigma}[m]$
for some m and asymmetric otherwise.
$\sigma= \overline{\sigma}[m]$
for some m and asymmetric otherwise.
Remark 6.2 By definition, any symmetric band
![]() $\sigma$
is a word such that
$\sigma$
is a word such that
where
![]() $t(a_r)$
and
$t(a_r)$
and
![]() $t(b_s)$
are special vertex, having the following picture:
$t(b_s)$
are special vertex, having the following picture:

Definition 6.3 A right (resp. left) infinite homotopy string is a sequence
![]() $\sigma = \sigma_0 \sigma_1 \sigma_2 \ldots $
(resp.
$\sigma = \sigma_0 \sigma_1 \sigma_2 \ldots $
(resp.
![]() $\sigma= \dots \sigma_{-2}\sigma_{-1} \sigma_0 $
) such that for some k, all
$\sigma= \dots \sigma_{-2}\sigma_{-1} \sigma_0 $
) such that for some k, all
![]() $\sigma_i$
(resp.
$\sigma_i$
(resp.
![]() $\sigma_{-i}$
) are direct (resp. inverse) arrows, for
$\sigma_{-i}$
) are direct (resp. inverse) arrows, for
![]() $i >k$
and such that every finite subword of
$i >k$
and such that every finite subword of
![]() $\sigma$
is a homotopy string.
$\sigma$
is a homotopy string.
An infinite homotopy string is a sequence
![]() $\sigma= \dots \sigma_{-2}\sigma_{-1}\sigma_0\sigma_1 \sigma_2 \dots$
such that
$\sigma= \dots \sigma_{-2}\sigma_{-1}\sigma_0\sigma_1 \sigma_2 \dots$
such that
![]() $\dots \sigma_{-2}\sigma_{-1}$
is a left infinite homotopy string and
$\dots \sigma_{-2}\sigma_{-1}$
is a left infinite homotopy string and
![]() $\sigma_0\sigma_1\sigma_{2}$
is a right infinite homotopy string.
$\sigma_0\sigma_1\sigma_{2}$
is a right infinite homotopy string.
6.2 String and Band Complexes
In order to define the complexes induced by homotopy strings and bands as introduced in [Reference Bekkert, Marcos and Merklen5], we need to introduce a grading on homotopy strings and bands. Our definition closely follows [Reference Opper, Plamondon and Schroll35].
Definition 6.4 Let
![]() $\sigma=\sigma_1 \dots \sigma_r$
be a finite homotopy string.
$\sigma=\sigma_1 \dots \sigma_r$
be a finite homotopy string.
A grading on
![]() $\sigma$
is a sequence of integers
$\sigma$
is a sequence of integers
![]() $\mu=(\mu_0, \dots, \mu_r)$
such that
$\mu=(\mu_0, \dots, \mu_r)$
such that
 \begin{equation*}\mu_{i+1}=\begin{cases} \mu_i+1 & \textrm{if $\sigma_{i+1}$ is a direct homotopy letter;}\\ \\[-7pt] \mu_{i}-1 & \textrm{otherwise,}\end{cases}\end{equation*}
\begin{equation*}\mu_{i+1}=\begin{cases} \mu_i+1 & \textrm{if $\sigma_{i+1}$ is a direct homotopy letter;}\\ \\[-7pt] \mu_{i}-1 & \textrm{otherwise,}\end{cases}\end{equation*}
for each
![]() $i\in \{1,\dots, r-1\}$
. The pair
$i\in \{1,\dots, r-1\}$
. The pair
![]() $(\sigma, \mu)$
is a graded homotopy string.
$(\sigma, \mu)$
is a graded homotopy string.
Moreover, if
![]() $\sigma$
is a homotopy band, the pair
$\sigma$
is a homotopy band, the pair
![]() $(\sigma, \mu)$
is a graded homotopy band if
$(\sigma, \mu)$
is a graded homotopy band if
![]() $(\sigma, \mu)$
is a graded homotopy string and i is considered modulo r.
$(\sigma, \mu)$
is a graded homotopy string and i is considered modulo r.
In a similar way, we define a grading on (left, right) infinite homotopy strings.
Let A be a skew-gentle algebra with admissible presentation
![]() $A^{sg} = KQ^{sg} / I^{sg}$
. For a vertex
$A^{sg} = KQ^{sg} / I^{sg}$
. For a vertex
![]() $i \in Q_0^{sg}$
, we write
$i \in Q_0^{sg}$
, we write
![]() $P_i$
for the projective indecomposable
$P_i$
for the projective indecomposable
![]() $A^{sg}$
-module at vertex i.
$A^{sg}$
-module at vertex i.
Following [Reference Bekkert, Marcos and Merklen5], to each graded homotopy string or band
![]() $(\sigma, \mu)$
we associate a complex of projective A-modules
$(\sigma, \mu)$
we associate a complex of projective A-modules
![]() $P^\bullet_{(\sigma, \mu)}$
which is not necessarily indecomposable, but is a sum of at most two indecomposable complexes. For this, we freely view A-modules as modules over
$P^\bullet_{(\sigma, \mu)}$
which is not necessarily indecomposable, but is a sum of at most two indecomposable complexes. For this, we freely view A-modules as modules over
![]() $A^{sg}$
and we define the following projective A-module for every
$A^{sg}$
and we define the following projective A-module for every
![]() $i \in Q_0$
.
$i \in Q_0$
.
 \begin{equation*}P(i)=\begin{cases}P_{i^+}\oplus P_{i^-} & \textrm{if {i} is a special vertex;}\\ \\[-7pt] P_i & \textrm{otherwise.}\end{cases}\end{equation*}
\begin{equation*}P(i)=\begin{cases}P_{i^+}\oplus P_{i^-} & \textrm{if {i} is a special vertex;}\\ \\[-7pt] P_i & \textrm{otherwise.}\end{cases}\end{equation*}
The definition of a complex associated with a symmetric homotopy band
![]() $\sigma$
relies on a set of matrices
$\sigma$
relies on a set of matrices
![]() $\mathcal{M}$
with coefficients in K where
$\mathcal{M}$
with coefficients in K where
![]() $M \in \mathcal{M}$
is such that
$M \in \mathcal{M}$
is such that
![]() $M=\begin{pmatrix} A &\quad C \\ B &\quad D\end{pmatrix}\in \textrm{Mat}(l+l', m+m')$
for some strictly positive integers l, l
$M=\begin{pmatrix} A &\quad C \\ B &\quad D\end{pmatrix}\in \textrm{Mat}(l+l', m+m')$
for some strictly positive integers l, l
![]() $^{\prime}$
,m,m
$^{\prime}$
,m,m
![]() $^{\prime}$
. We refer the reader to [Reference Bekkert, Marcos and Merklen5, Section 3.1] for the precise definition of
$^{\prime}$
. We refer the reader to [Reference Bekkert, Marcos and Merklen5, Section 3.1] for the precise definition of
![]() $\mathcal{M}$
.
$\mathcal{M}$
.
Definition 6.5
-
1. Let
 $(\sigma,\mu)$
be a graded homotopy string with
$(\sigma,\mu)$
be a graded homotopy string with
 $\sigma=\sigma_1 \dots \sigma_r$
. Then let be the complex such that
$\sigma=\sigma_1 \dots \sigma_r$
. Then let be the complex such that \begin{equation*}P^\bullet_{(\sigma, \mu)}= \dots \longrightarrow P^{-1} \longrightarrow P^0 \longrightarrow P^1 \longrightarrow \dots\end{equation*}
\begin{equation*}P^\bullet_{(\sigma, \mu)}= \dots \longrightarrow P^{-1} \longrightarrow P^0 \longrightarrow P^1 \longrightarrow \dots\end{equation*}
 $P^j=\bigoplus_{\substack{0\leq i \leq r \\ \mu_i=j}} P(i)$
, for all
$P^j=\bigoplus_{\substack{0\leq i \leq r \\ \mu_i=j}} P(i)$
, for all
 $j \in \mathbb Z$
and where the differentials are induced by the homotopy letters.
$j \in \mathbb Z$
and where the differentials are induced by the homotopy letters.
If
 $\sigma$
is an asymmetric homotopy string, we say that a complex P is an asymmetric string complex if it is isomorphic to
$\sigma$
is an asymmetric homotopy string, we say that a complex P is an asymmetric string complex if it is isomorphic to
 $P_{(\sigma, \mu)}$
in
$P_{(\sigma, \mu)}$
in
 $K^{b,-}(proj - A)$
.
$K^{b,-}(proj - A)$
.If
 $\sigma$
is a symmetric homotopy string, then
$\sigma$
is a symmetric homotopy string, then
 $P_{(\sigma, \mu)}$
decomposes into the direct sum of two indecomposables complexes of projective A-modules. We will refer to the indecomposable summands as
$P_{(\sigma, \mu)}$
decomposes into the direct sum of two indecomposables complexes of projective A-modules. We will refer to the indecomposable summands as
 $P_{(\sigma, \mu,0)}$
and
$P_{(\sigma, \mu,0)}$
and
 $P_{(\sigma, \mu,1)}$
. We call a complex P isomorphic to either
$P_{(\sigma, \mu,1)}$
. We call a complex P isomorphic to either
 $P_{(\sigma, \mu, 0)}^{\bullet}$
or
$P_{(\sigma, \mu, 0)}^{\bullet}$
or
 $P_{(\sigma, \mu, 1)}^{\bullet}$
, a dimidiate string complex.
$P_{(\sigma, \mu, 1)}^{\bullet}$
, a dimidiate string complex.
-
2. Let
 $(\sigma, \mu)$
be a graded homotopy band where
$(\sigma, \mu)$
be a graded homotopy band where
 $\sigma=\sigma_1 \dots \sigma_r$
is an asymmetric homotopy band. Let
$\sigma=\sigma_1 \dots \sigma_r$
is an asymmetric homotopy band. Let
 $\operatorname{ind}K\left[x\right]$
be the set of non-trivial powers of irreducible polynomials over K with leading coefficient equal to 1 and different from x and
$\operatorname{ind}K\left[x\right]$
be the set of non-trivial powers of irreducible polynomials over K with leading coefficient equal to 1 and different from x and
 $x-1$
. Then, for each
$x-1$
. Then, for each
 $p(x)\in \operatorname{ind}k\left[x\right]$
, let be the complex such that
$p(x)\in \operatorname{ind}k\left[x\right]$
, let be the complex such that \begin{equation*}P^\bullet_{(\sigma, \mu), p(x)}= \dots \longrightarrow P^{-1} \longrightarrow P^0 \longrightarrow P^1 \longrightarrow \dots\end{equation*}
\begin{equation*}P^\bullet_{(\sigma, \mu), p(x)}= \dots \longrightarrow P^{-1} \longrightarrow P^0 \longrightarrow P^1 \longrightarrow \dots\end{equation*}
 $P^j=\bigoplus_{\substack{0\leq i \leq r \\ \mu_i=j}} P(i) \otimes_K K^{\operatorname{deg} p(x)}$
in degree j. We call a complex P an asymmetric band complex if it is isomorphic in
$P^j=\bigoplus_{\substack{0\leq i \leq r \\ \mu_i=j}} P(i) \otimes_K K^{\operatorname{deg} p(x)}$
in degree j. We call a complex P an asymmetric band complex if it is isomorphic in
 $K^{b,-}(proj - A)$
to
$K^{b,-}(proj - A)$
to
 $P_{(\sigma, \mu), p(x)}$
where
$P_{(\sigma, \mu), p(x)}$
where
 $\sigma$
is an asymmetric band.
$\sigma$
is an asymmetric band.
-
3. Let
 $(\sigma, \mu)$
be a graded homotopy band with
$(\sigma, \mu)$
be a graded homotopy band with
 $\sigma=a_1 \dots a_r\overline{a_r}\dots \overline{a_1}b_1 \dots b_s \overline{b_s} \dots \overline{b_1}$
symmetric and such that
$\sigma=a_1 \dots a_r\overline{a_r}\dots \overline{a_1}b_1 \dots b_s \overline{b_s} \dots \overline{b_1}$
symmetric and such that
 $e(a_r)$
and
$e(a_r)$
and
 $e(b_s)$
are special vertices. Let
$e(b_s)$
are special vertices. Let
 $M=\begin{pmatrix} A & \quad C \\ B &\quad D\end{pmatrix}\in \mathcal M$
. Then the complexis given by
$M=\begin{pmatrix} A & \quad C \\ B &\quad D\end{pmatrix}\in \mathcal M$
. Then the complexis given by \begin{equation*}P^\bullet_{(\sigma, \mu)}= \dots \longrightarrow P^{-1} \longrightarrow P^0 \longrightarrow P^1 \longrightarrow \dots\end{equation*}
\begin{equation*}P^\bullet_{(\sigma, \mu)}= \dots \longrightarrow P^{-1} \longrightarrow P^0 \longrightarrow P^1 \longrightarrow \dots\end{equation*}
 \begin{equation*}P^j=\bigoplus_{\substack{0\leq i \leq r \\ \mu_i=j}} Q(i)\oplus \bigoplus_{\substack{2r+1\leq i \leq 2r+s \\ \mu_i=j}} Q(i)\end{equation*}
\begin{equation*}P^j=\bigoplus_{\substack{0\leq i \leq r \\ \mu_i=j}} Q(i)\oplus \bigoplus_{\substack{2r+1\leq i \leq 2r+s \\ \mu_i=j}} Q(i)\end{equation*}
for all
 $j\in \mathbb Z$
, where Q(i) is a projective A-module which depends on the size of the matrices A,B,C,D in M as follows:
$j\in \mathbb Z$
, where Q(i) is a projective A-module which depends on the size of the matrices A,B,C,D in M as follows: \begin{equation*}Q(i)=\begin{cases} P(i)\otimes_K K^{l} \oplus P(i)\otimes_K K^{l'} & \textrm{if $i=\mu_0, \dots, \mu_{r-1}$}\\ \\[-7pt] P(i)\otimes_K K^{m} \oplus P(i)\otimes_K K^{m'} & \textrm{if $i=\mu_{2r+1}, \dots, \mu_{2r+s-1}$}\\ \\[-7pt] P_{i^+}\otimes_K K^{l} \oplus P_{i^-}\otimes_K K^{l'} & \textrm{if $i=\mu_{r}$}\\ \\[-7pt] P_{i^+}\otimes_K K^{m} \oplus P_{i^-}\otimes_K K^{m'} & \textrm{if $i=2r+s$}\end{cases}.\end{equation*}
\begin{equation*}Q(i)=\begin{cases} P(i)\otimes_K K^{l} \oplus P(i)\otimes_K K^{l'} & \textrm{if $i=\mu_0, \dots, \mu_{r-1}$}\\ \\[-7pt] P(i)\otimes_K K^{m} \oplus P(i)\otimes_K K^{m'} & \textrm{if $i=\mu_{2r+1}, \dots, \mu_{2r+s-1}$}\\ \\[-7pt] P_{i^+}\otimes_K K^{l} \oplus P_{i^-}\otimes_K K^{l'} & \textrm{if $i=\mu_{r}$}\\ \\[-7pt] P_{i^+}\otimes_K K^{m} \oplus P_{i^-}\otimes_K K^{m'} & \textrm{if $i=2r+s$}\end{cases}.\end{equation*}
We say that a complex P is a dimidiate band complex if it is isomorphic in
 $K^{b,-}(proj - A)$
to
$K^{b,-}(proj - A)$
to
 $P_{(\sigma, \mu), M}$
where
$P_{(\sigma, \mu), M}$
where
 $\sigma$
is a symmetric band.
$\sigma$
is a symmetric band.
We will not give the definitions of the differentials of the above complexes, since we do not need those in the geometric description of the indecomposable objects of the bounded derived category of a skew-gentle algebra.
Remark 6.6 In [Reference Schroll and Valdivieso39], we give a correspondence of intersections of graded curves and homomorphisms in the bounded derived category of a skew-gentle algebra.
For a grading
![]() $\mu= (\mu_1, \ldots, \mu_r)$
on a homotopy string or band, define a grading shift [m] as
$\mu= (\mu_1, \ldots, \mu_r)$
on a homotopy string or band, define a grading shift [m] as
![]() $\mu[m] = (\mu_1 +m, \ldots, \mu_r +m)$
for
$\mu[m] = (\mu_1 +m, \ldots, \mu_r +m)$
for
![]() $m \in \mathbb{Z}$
. Observe that the complex induced by
$m \in \mathbb{Z}$
. Observe that the complex induced by
![]() $(\sigma, \mu[m])$
is
$(\sigma, \mu[m])$
is
![]() $P^\bullet_{(\sigma, \mu[m])}=P^\bullet_{(\sigma, \mu)}[m]$
.
$P^\bullet_{(\sigma, \mu[m])}=P^\bullet_{(\sigma, \mu)}[m]$
.
6.3 Main result on indecomposable objects of the derived category of a skew-gentle algebra
Before stating one of the main theorems of this paper, we recall that we identify unmarked boundary components and punctures in a surface S. We also recall that given an orbifold dissection
![]() $O=(S,M,\mathcal O, G)$
we define graded arcs and graded closed curves up to O-homotopy.
$O=(S,M,\mathcal O, G)$
we define graded arcs and graded closed curves up to O-homotopy.
Theorem 6.7 Let A be a skew-gentle algebra with orbifold dissection
![]() $O=(S, M, \mathcal{O}, G^*)$
. Then the homotopy strings and bands parametrising the indecomposable objects in
$O=(S, M, \mathcal{O}, G^*)$
. Then the homotopy strings and bands parametrising the indecomposable objects in
![]() $D^b(A)$
are in bijection with graded arcs and curves in O. More precisely,
$D^b(A)$
are in bijection with graded arcs and curves in O. More precisely,
-
(1) the set of homotopy strings are in bijection with graded arcs
 $(\gamma, f)$
, where
$(\gamma, f)$
, where
 $\gamma$
is a finite arc in O or an infinite arc whose infinite rays wrap around unmarked boundary components in the anti-clockwise orientation;
$\gamma$
is a finite arc in O or an infinite arc whose infinite rays wrap around unmarked boundary components in the anti-clockwise orientation; -
(2) the set of homotopy bands are in bijection with graded primitive closed curves
 $(\gamma, f)$
in O.
$(\gamma, f)$
in O.
The proof is very similar to that of the corresponding result for gentle algebras in [Reference Opper, Plamondon and Schroll35] with suitable adjustments to be made for special loops in the algebra on the one side and polygons containing orbifold points in the surface on the other. For the convenience of the reader, we give the whole proof in detail.
The following definition gives the construction of a homotopy word induced by the intersection of an arc or curve in the surface with the edges of the dual graph.
Definition 6.8 Let A be a skew-gentle algebra with quiver
![]() $Q_A=Q$
and
$Q_A=Q$
and
![]() $\gamma$
be an arc or a closed curve in its orbifold dissection
$\gamma$
be an arc or a closed curve in its orbifold dissection
![]() $(S,M, \mathcal{O}, G^*)$
. We set
$(S,M, \mathcal{O}, G^*)$
. We set
![]() $\left(x_i\right)$
to be the ordered multiset of edges of
$\left(x_i\right)$
to be the ordered multiset of edges of
![]() $G^*$
crossed by
$G^*$
crossed by
![]() $\gamma$
following its trajectory. Furthermore, if
$\gamma$
following its trajectory. Furthermore, if
![]() $\gamma$
crosses
$\gamma$
crosses
![]() $G^*$
at least twice. Let
$G^*$
at least twice. Let
![]() $\left[x_{i}, x_{i+1}\right]$
be the oriented segment going from
$\left[x_{i}, x_{i+1}\right]$
be the oriented segment going from
![]() $x_i$
to
$x_i$
to
![]() $x_{i+1}$
, recall that both edges are in a (degenerate) polygon P which contains exactly one marked point
$x_{i+1}$
, recall that both edges are in a (degenerate) polygon P which contains exactly one marked point
![]() $m \in M$
.
$m \in M$
.
We define the homotopy letter
![]() $\sigma(x_i)$
associated with the oriented segment
$\sigma(x_i)$
associated with the oriented segment
![]() $\left[x_i, x_{i+1}\right]$
as follows:
$\left[x_i, x_{i+1}\right]$
as follows:
-
1. If the marked point m is on the left of
 $\left[x_i, x_{i+1}\right]$
, then let
$\left[x_i, x_{i+1}\right]$
, then let
 $w_1, \dots, w_r$
be the edges between
$w_1, \dots, w_r$
be the edges between
 $x_i=w_1$
and
$x_i=w_1$
and
 $x_{i+1}=w_r$
in the clockwise order. By Theorem 4.8, these correspond to vertices of the quiver Q of A which are joined by arrows
$x_{i+1}=w_r$
in the clockwise order. By Theorem 4.8, these correspond to vertices of the quiver Q of A which are joined by arrows
 $\alpha_1, \dots, \alpha_{r-1}$
. Then define
$\alpha_1, \dots, \alpha_{r-1}$
. Then define
 $\sigma(x_i):=(\alpha_1 \dots \alpha_{r-1})$
.
$\sigma(x_i):=(\alpha_1 \dots \alpha_{r-1})$
. -
2. If the marked point m is on the right of
 $\left[x_i, x_{i+1}\right]$
, then let
$\left[x_i, x_{i+1}\right]$
, then let
 $w_1, \dots, w_r$
be the edges between
$w_1, \dots, w_r$
be the edges between
 $x_{i+1}=w_1$
and
$x_{i+1}=w_1$
and
 $x_i=w_r$
in the clockwise order. By Theorem 4.8, these correspond to vertices of the quiver Q of A which are joined by arrows
$x_i=w_r$
in the clockwise order. By Theorem 4.8, these correspond to vertices of the quiver Q of A which are joined by arrows
 $\alpha_1, \dots, \alpha_{r-1}$
. Then define
$\alpha_1, \dots, \alpha_{r-1}$
. Then define
 $\sigma(x_i):=\overline{(\alpha_1 \dots \alpha_{r-1})}$
.
$\sigma(x_i):=\overline{(\alpha_1 \dots \alpha_{r-1})}$
.
If a graded arc
![]() $(\gamma, f)$
crosses
$(\gamma, f)$
crosses
![]() $G^*$
exactly once, namely at the edge x, then we set
$G^*$
exactly once, namely at the edge x, then we set
![]() $\sigma(\gamma)$
to be the trivial string
$\sigma(\gamma)$
to be the trivial string
![]() $e_x$
, and
$e_x$
, and
![]() $\mu(f)=(f(x))$
the grading on
$\mu(f)=(f(x))$
the grading on
![]() $\sigma(\gamma)$
.
$\sigma(\gamma)$
.
Observe that by Theorem 4.8,
![]() $\sigma(x_i)$
is indeed a homotopy letter.
$\sigma(x_i)$
is indeed a homotopy letter.
Lemma 6.9 Let
![]() $(S, M, \mathcal{O}, G^*)$
be the orbifold dissection of a skew-gentle algebra A given by the dual
$(S, M, \mathcal{O}, G^*)$
be the orbifold dissection of a skew-gentle algebra A given by the dual
![]() $G^*$
of the generalised ribbon graph of A and let
$G^*$
of the generalised ribbon graph of A and let
![]() $(\gamma, f)$
be an arc or a graded primitive closed curve on
$(\gamma, f)$
be an arc or a graded primitive closed curve on
![]() $(S,M,\mathcal{O})$
with
$(S,M,\mathcal{O})$
with
![]() $\left(x_i \right)$
the ordered multiset of edges of the dual graph
$\left(x_i \right)$
the ordered multiset of edges of the dual graph
![]() $G^*$
crossed by
$G^*$
crossed by
![]() $\gamma$
following its trajectory.
$\gamma$
following its trajectory.
-
(1) If
 $(\gamma, f)$
is a finite graded arc which crosses the edges of
$(\gamma, f)$
is a finite graded arc which crosses the edges of
 $G^*$
exactly r times and at least twice, then
$G^*$
exactly r times and at least twice, then
 $\sigma(\gamma)= \prod_{i=1}^{r-1}\sigma(x_i)$
is a homotopy string and
$\sigma(\gamma)= \prod_{i=1}^{r-1}\sigma(x_i)$
is a homotopy string and
 $\mu(f) = (f(x_1),\dots,f(x_r))$
is a grading on
$\mu(f) = (f(x_1),\dots,f(x_r))$
is a grading on
 $\sigma(\gamma)$
.
$\sigma(\gamma)$
. -
(2) If
 $(\gamma, f)$
is an infinite graded arc, then
$(\gamma, f)$
is an infinite graded arc, then
 $\sigma(\gamma)=\prod\sigma(x_i)$
is a infinite homotopy string and
$\sigma(\gamma)=\prod\sigma(x_i)$
is a infinite homotopy string and
 $\mu(f) = (f(x_i))$
is a grading on
$\mu(f) = (f(x_i))$
is a grading on
 $\sigma(\gamma)$
.
$\sigma(\gamma)$
. -
(3) If
 $(\gamma, f)$
is a primitive graded closed curve and if
$(\gamma, f)$
is a primitive graded closed curve and if
 $x_1, x_2, \dots, x_r$
are the distinct edges of
$x_1, x_2, \dots, x_r$
are the distinct edges of
 $G^*$
crossed by
$G^*$
crossed by
 $\gamma$
(in that order), then
$\gamma$
(in that order), then
 $\sigma(\gamma)=\prod_{i=0}^r\sigma(x_i)$
is a homotopy band and
$\sigma(\gamma)=\prod_{i=0}^r\sigma(x_i)$
is a homotopy band and
 $\mu(f) = (f(x_1),\dots,f(x_{r-1}))$
is a grading on
$\mu(f) = (f(x_1),\dots,f(x_{r-1}))$
is a grading on
 $\sigma(\gamma)$
.
$\sigma(\gamma)$
.
Proof. By construction,
![]() $\sigma(\gamma_i)$
is a homotopy letter, for all i. As before, let
$\sigma(\gamma_i)$
is a homotopy letter, for all i. As before, let
![]() $\Lambda= KQ/I$
be the associated gentle algebra obtained from A be deleting all special loops, B be a minimal set of relations of
$\Lambda= KQ/I$
be the associated gentle algebra obtained from A be deleting all special loops, B be a minimal set of relations of
![]() $\Lambda$
and
$\Lambda$
and
![]() $A+ = KQ/J$
, where
$A+ = KQ/J$
, where
![]() $J = \langle B \setminus \{\alpha \beta \mid t(\alpha) \in Sp \}\rangle$
. By Theorem 4.8, either the composition or of the last arrow of
$J = \langle B \setminus \{\alpha \beta \mid t(\alpha) \in Sp \}\rangle$
. By Theorem 4.8, either the composition or of the last arrow of
![]() $\sigma(\gamma_i)$
and the first arrow of
$\sigma(\gamma_i)$
and the first arrow of
![]() $\sigma(\gamma_{i+1})$
(or the composition of their inverses) are in J or the end of
$\sigma(\gamma_{i+1})$
(or the composition of their inverses) are in J or the end of
![]() $\sigma(\gamma_i)$
is a special vertex. Then (2) directly follows from the definition of homotopy strings in Section 6.1.
$\sigma(\gamma_i)$
is a special vertex. Then (2) directly follows from the definition of homotopy strings in Section 6.1.
Now let
![]() $(\gamma, f)$
be an infinite graded arc. By Lemma 5.3,
$(\gamma, f)$
be an infinite graded arc. By Lemma 5.3,
![]() $\gamma$
wraps around a puncture p with at least one incident edge and by the above, every finite homotopy sub-walk of
$\gamma$
wraps around a puncture p with at least one incident edge and by the above, every finite homotopy sub-walk of
![]() $\sigma(\gamma)$
is a homotopy string. Denote by
$\sigma(\gamma)$
is a homotopy string. Denote by
![]() $x_k, x_{k+1}, \dots, x_r$
the set of edges of
$x_k, x_{k+1}, \dots, x_r$
the set of edges of
![]() $G^*$
that
$G^*$
that
![]() $\gamma$
crosses when
$\gamma$
crosses when
![]() $\gamma$
does a complete turn around p. By Theorem 4.8, their associated homotopy letters
$\gamma$
does a complete turn around p. By Theorem 4.8, their associated homotopy letters
![]() $\sigma(x_k), \dots, \sigma(x_r)$
are homotopy letters of length one, and
$\sigma(x_k), \dots, \sigma(x_r)$
are homotopy letters of length one, and
![]() $\sigma(x_k) \dots \sigma(x_r)$
or its inverse is an oriented cycle. Furthermore, we have that
$\sigma(x_k) \dots \sigma(x_r)$
or its inverse is an oriented cycle. Furthermore, we have that
![]() $\sigma(x_r) \sigma(x_{r+1}) \in J$
with
$\sigma(x_r) \sigma(x_{r+1}) \in J$
with
![]() $\sigma(x_{r+1}) = \sigma(x_{k})$
and more generally,
$\sigma(x_{r+1}) = \sigma(x_{k})$
and more generally,
![]() $\sigma(x_{r+i}) = \sigma(x_{k+i-1})$
for all
$\sigma(x_{r+i}) = \sigma(x_{k+i-1})$
for all
![]() $i \geq 1$
. Thus,
$i \geq 1$
. Thus,
![]() $\sigma(\gamma)$
is eventually periodic and an infinite homotopy string.
$\sigma(\gamma)$
is eventually periodic and an infinite homotopy string.
In cases (1) and (2), directly follows from the definition of the grading f on
![]() $\gamma$
that
$\gamma$
that
![]() $\mu(f)$
is a grading on the associated homotopy string.
$\mu(f)$
is a grading on the associated homotopy string.
To prove (3), assume that
![]() $(\gamma, f)$
is a graded primitive closed curve. Let
$(\gamma, f)$
is a graded primitive closed curve. Let
![]() $\sigma(\gamma)=\prod_{i=0}^r\sigma(\gamma_i)$
. It is enough to observe that
$\sigma(\gamma)=\prod_{i=0}^r\sigma(\gamma_i)$
. It is enough to observe that
![]() $s(\sigma(\gamma_1))=t(\sigma_{\gamma_r})$
to ensure that any rotation of
$s(\sigma(\gamma_1))=t(\sigma_{\gamma_r})$
to ensure that any rotation of
![]() $\sigma(\gamma)$
is a homotopy string. By definition, the existence of the grading f implies that there is the same number of inverse and direct homotopy letters in
$\sigma(\gamma)$
is a homotopy string. By definition, the existence of the grading f implies that there is the same number of inverse and direct homotopy letters in
![]() $\sigma(\gamma)$
, which implies that
$\sigma(\gamma)$
, which implies that
![]() $\sigma(\gamma)$
is a homotopy band.
$\sigma(\gamma)$
is a homotopy band.
Lemma 6.10 Let
![]() $O=(S,M, \mathcal{O}, G^*)$
be the orbifold dissection of a skew-gentle algebra A given by the dual graph generalised ribbon graph
$O=(S,M, \mathcal{O}, G^*)$
be the orbifold dissection of a skew-gentle algebra A given by the dual graph generalised ribbon graph
![]() $G^*$
of A.
$G^*$
of A.
-
(1) Let
 $(\sigma, \mu)$
be a finite (resp. infinite) graded homotopy string. Then there exists a unique finite (resp. infinite) graded arc
$(\sigma, \mu)$
be a finite (resp. infinite) graded homotopy string. Then there exists a unique finite (resp. infinite) graded arc
 $(\gamma, f)$
on O such that
$(\gamma, f)$
on O such that
 $(\sigma(\gamma), \mu(f))=(\sigma, \mu)$
.
$(\sigma(\gamma), \mu(f))=(\sigma, \mu)$
. -
(2) Let
 $(\sigma,\mu)$
be a graded homotopy band. Then there exists a unique graded closed curve
$(\sigma,\mu)$
be a graded homotopy band. Then there exists a unique graded closed curve
 $(\gamma, f)$
on O (up to O-homotopy) such that
$(\gamma, f)$
on O (up to O-homotopy) such that
 $(\sigma(\gamma), \mu(f))=(\sigma, \mu)$
.
$(\sigma(\gamma), \mu(f))=(\sigma, \mu)$
.
Proof. Let
![]() $\Lambda= KQ/I$
be the associated gentle algebra obtained from A be deleting all special loops, B be a minimal set of relations of
$\Lambda= KQ/I$
be the associated gentle algebra obtained from A be deleting all special loops, B be a minimal set of relations of
![]() $\Lambda$
and
$\Lambda$
and
![]() $A+ = KQ/J$
, where
$A+ = KQ/J$
, where
![]() $J = \langle B \setminus \{\alpha \beta \mid t(\alpha) \in Sp \}\rangle$
.
$J = \langle B \setminus \{\alpha \beta \mid t(\alpha) \in Sp \}\rangle$
.
Let
![]() $(\sigma, \mu)$
be a finite graded homotopy string. By definition
$(\sigma, \mu)$
be a finite graded homotopy string. By definition
![]() $\sigma$
is a sequence
$\sigma$
is a sequence
![]() $\sigma_1 \dots \sigma_n$
of homotopy letters
$\sigma_1 \dots \sigma_n$
of homotopy letters
![]() $\sigma_i$
where
$\sigma_i$
where
![]() $s(\sigma_{i+1})=t(\sigma_i)$
and such that either
$s(\sigma_{i+1})=t(\sigma_i)$
and such that either
![]() $\sigma_i\sigma_{i+1}\in J$
or
$\sigma_i\sigma_{i+1}\in J$
or
![]() $\overline{\sigma_i\sigma_{i+1}}\in J$
or
$\overline{\sigma_i\sigma_{i+1}}\in J$
or
![]() $s(\sigma_{i+1})=t(\sigma_i)$
is a special vertex.
$s(\sigma_{i+1})=t(\sigma_i)$
is a special vertex.
It is enough to prove that for each homotopy letter
![]() $\sigma_i$
there is a (unique) oriented segment
$\sigma_i$
there is a (unique) oriented segment
![]() $\gamma_i$
such that the topological concatenation of those segments induces a graded arc
$\gamma_i$
such that the topological concatenation of those segments induces a graded arc
![]() $\gamma$
on O and that two distinct homotopy strings give rise to two graded arcs which are not O-homotopic.
$\gamma$
on O and that two distinct homotopy strings give rise to two graded arcs which are not O-homotopic.
Denote by
![]() $x_i$
and
$x_i$
and
![]() $x_{i+1}$
the edges of
$x_{i+1}$
the edges of
![]() $G^*$
corresponding to
$G^*$
corresponding to
![]() $s(\sigma_i)$
and
$s(\sigma_i)$
and
![]() $t(\sigma_i)$
respectively. By construction of
$t(\sigma_i)$
respectively. By construction of
![]() $G^*$
, there is exactly one (degenerate) polygon
$G^*$
, there is exactly one (degenerate) polygon
![]() $P_i$
in O such that
$P_i$
in O such that
![]() $x_i$
and
$x_i$
and
![]() $x_{i+1}$
are edges of
$x_{i+1}$
are edges of
![]() $P_i$
.
$P_i$
.
If
![]() $P_i$
is not degenerate or
$P_i$
is not degenerate or
![]() $x_i$
and
$x_i$
and
![]() $x_{i+1}$
are not special edges, then up to homotopy there is a unique oriented segment
$x_{i+1}$
are not special edges, then up to homotopy there is a unique oriented segment
![]() $\gamma_i$
in the interior of
$\gamma_i$
in the interior of
![]() $P_i$
starting at the mid-point of
$P_i$
starting at the mid-point of
![]() $x_i$
and ending at the mid-point of
$x_i$
and ending at the mid-point of
![]() $x_{i+1}$
such that
$x_{i+1}$
such that
![]() $\gamma_i$
has no self-crossing and does not cross any other edge of
$\gamma_i$
has no self-crossing and does not cross any other edge of
![]() $G^*$
.
$G^*$
.
If
![]() $x_i$
is not a special edge and
$x_i$
is not a special edge and
![]() $x_{i+1}$
is a special edge (or
$x_{i+1}$
is a special edge (or
![]() $x_i$
is a special edge and
$x_i$
is a special edge and
![]() $x_{i+1}$
is not a special edge), then up to homotopy there is a unique oriented segment
$x_{i+1}$
is not a special edge), then up to homotopy there is a unique oriented segment
![]() $\gamma_i$
in the interior of
$\gamma_i$
in the interior of
![]() $P_i$
starting at the mid-point of (resp. the orbifold point of the edge)
$P_i$
starting at the mid-point of (resp. the orbifold point of the edge)
![]() $x_i$
and ending at the orbifold point of the edge (resp. the mid-point of)
$x_i$
and ending at the orbifold point of the edge (resp. the mid-point of)
![]() $x_{i+1}$
such that
$x_{i+1}$
such that
![]() $\gamma_i$
has no self-crossing and does not cross any other edge of
$\gamma_i$
has no self-crossing and does not cross any other edge of
![]() $G^*$
, see Figure 10.
$G^*$
, see Figure 10.

Figure 10. The arc
![]() $\gamma$
from
$\gamma$
from
![]() $x_i$
to
$x_i$
to
![]() $x_{i+1}$
.
$x_{i+1}$
.
It is clear that the ending point of the oriented segment
![]() $\gamma_i$
is the starting point of
$\gamma_i$
is the starting point of
![]() $\gamma_{i+1}$
and that the concatenation
$\gamma_{i+1}$
and that the concatenation
![]() $\gamma_{1}*\dots *\gamma_{n}$
is an oriented segment from
$\gamma_{1}*\dots *\gamma_{n}$
is an oriented segment from
![]() $x_1=s(\sigma_1\dots \sigma_n)$
to
$x_1=s(\sigma_1\dots \sigma_n)$
to
![]() $x_{n+1}=t(\sigma_1 \dots \sigma_n)$
.
$x_{n+1}=t(\sigma_1 \dots \sigma_n)$
.
Now, let
![]() $P_0$
(resp.
$P_0$
(resp.
![]() $P_{n+1}$
) be the (degenerate) polygon which shares
$P_{n+1}$
) be the (degenerate) polygon which shares
![]() $x_1$
(resp.
$x_1$
(resp.
![]() $x_{n+1}$
) with
$x_{n+1}$
) with
![]() $P_1$
(resp.
$P_1$
(resp.
![]() $P_n$
) and let
$P_n$
) and let
![]() $m_0$
(resp.
$m_0$
(resp.
![]() $m_{n+1}$
) be the marked point in the boundary segment of
$m_{n+1}$
) be the marked point in the boundary segment of
![]() $P_0$
(resp.
$P_0$
(resp.
![]() $P_{x_{n+1}}$
). Observe that if
$P_{x_{n+1}}$
). Observe that if
![]() $x_1$
(resp.
$x_1$
(resp.
![]() $x_n$
) is a special edge, then
$x_n$
) is a special edge, then
![]() $P_0$
and
$P_0$
and
![]() $P_1$
(resp.
$P_1$
(resp.
![]() $P_n$
and
$P_n$
and
![]() $P_{n+1}$
) coincide.
$P_{n+1}$
) coincide.
Suppose that
![]() $x_1$
(resp.
$x_1$
(resp.
![]() $x_n$
) is not a special edge, then there exists a unique oriented segment from the marked point
$x_n$
) is not a special edge, then there exists a unique oriented segment from the marked point
![]() $m_0$
(resp. the point
$m_0$
(resp. the point
![]() $x_{n+1}$
) to middle point of
$x_{n+1}$
) to middle point of
![]() $x_1$
(resp. marked point
$x_1$
(resp. marked point
![]() $m_{n+1}$
), which lies in
$m_{n+1}$
), which lies in
![]() $P_0$
(resp.
$P_0$
(resp.
![]() $P_{n+1}$
), without self intersection and it is not crossing other edge of
$P_{n+1}$
), without self intersection and it is not crossing other edge of
![]() $G^*$
.
$G^*$
.
If
![]() $x_1$
(resp.
$x_1$
(resp.
![]() $x_n$
) is a special edge, then there is a unique oriented segment
$x_n$
) is a special edge, then there is a unique oriented segment
![]() $\gamma_0$
(resp.
$\gamma_0$
(resp.
![]() $\gamma_{n+1}$
) from
$\gamma_{n+1}$
) from
![]() $m_0$
(resp. the middle point of
$m_0$
(resp. the middle point of
![]() $x_{n+1}$
) to the orbifold point of
$x_{n+1}$
) to the orbifold point of
![]() $x_1$
(resp.
$x_1$
(resp.
![]() $m_{n+1}$
) such that
$m_{n+1}$
) such that
![]() $\gamma_0*\gamma_1$
(resp.
$\gamma_0*\gamma_1$
(resp.
![]() $\gamma_{n}*\gamma_{n+1}$
)lies in
$\gamma_{n}*\gamma_{n+1}$
)lies in
![]() $P_1=P_0$
(resp.
$P_1=P_0$
(resp.
![]() $P_{n}=P_{n+1}$
) and is not crossing any other edge of
$P_{n}=P_{n+1}$
) and is not crossing any other edge of
![]() $G^*$
, see Figure 11.
$G^*$
, see Figure 11.

Figure 11. Oriented segment
![]() $\gamma_0*\gamma_1.$
$\gamma_0*\gamma_1.$
Then,
![]() $\gamma=\gamma_0*\gamma_1* \dots * \gamma_{n}*\gamma_{n+1}$
is a finite arc and by construction
$\gamma=\gamma_0*\gamma_1* \dots * \gamma_{n}*\gamma_{n+1}$
is a finite arc and by construction
![]() $\sigma(\gamma)=\sigma$
. Moreover, the grading
$\sigma(\gamma)=\sigma$
. Moreover, the grading
![]() $\mu$
on
$\mu$
on
![]() $\sigma$
induces a natural grading f on
$\sigma$
induces a natural grading f on
![]() $\gamma$
.
$\gamma$
.
To finish the proof, suppose that
![]() $\gamma'$
is a finite arcs such that
$\gamma'$
is a finite arcs such that
![]() $\sigma(\gamma')=\sigma=\sigma(\gamma)$
. Without loss of generality, suppose that
$\sigma(\gamma')=\sigma=\sigma(\gamma)$
. Without loss of generality, suppose that
![]() $\gamma'$
is in minimal position, then
$\gamma'$
is in minimal position, then
![]() $\sigma(\gamma')$
is already a reduced homotopy string. We claim that
$\sigma(\gamma')$
is already a reduced homotopy string. We claim that
![]() $\gamma$
and
$\gamma$
and
![]() $\gamma'$
are O-homotopic. Any curve is completely determined by the ordered multiset of edges of
$\gamma'$
are O-homotopic. Any curve is completely determined by the ordered multiset of edges of
![]() $G^*$
that it crosses and
$G^*$
that it crosses and
![]() $\sigma(\gamma')=\sigma=\sigma(\gamma)$
, thus
$\sigma(\gamma')=\sigma=\sigma(\gamma)$
, thus
![]() $\gamma$
and
$\gamma$
and
![]() $\gamma'$
have the same multiset of edges of crossings with
$\gamma'$
have the same multiset of edges of crossings with
![]() $G^*$
and
$G^*$
and
![]() $\gamma$
and
$\gamma$
and
![]() $\gamma'$
are O-homotopic.
$\gamma'$
are O-homotopic.
The proof for infinite homotopy strings and bands is similar to the above.
Proof of Theorem 6.7. By [Reference Bekkert, Marcos and Merklen5, Theorem 3], the indecomposable objects of the derived category
![]() $\mathcal D^b(A)$
are completely described by the graded homotopy strings and bands. The result then follows from Lemma 6.9 and Lemma 6.10.
$\mathcal D^b(A)$
are completely described by the graded homotopy strings and bands. The result then follows from Lemma 6.9 and Lemma 6.10.
7. Applications
7.1 Singularity category of a skew-gentle algebra
The stable derived category or singularity category
![]() $\mathcal D_{sg}(A)$
of an algebra A is defined as the Verdier quotient of the bounded derived category with respect to the perfect derived category.
$\mathcal D_{sg}(A)$
of an algebra A is defined as the Verdier quotient of the bounded derived category with respect to the perfect derived category.
In [Reference Kalck27, Theorem 2.5], the singularity category of a gentle algebra was explicitly described as a finite product of triangulated orbit categories which turn out to be n-cluster categories of type
![]() $\mathbb A_1$
, as follows. Let
$\mathbb A_1$
, as follows. Let
![]() $\Lambda=KQ/I$
be a gentle algebra. A cycle
$\Lambda=KQ/I$
be a gentle algebra. A cycle
![]() $\alpha_1 \dots \alpha_n$
of positive length on Q is saturated if each of the length-2 paths
$\alpha_1 \dots \alpha_n$
of positive length on Q is saturated if each of the length-2 paths
![]() $\alpha_{1}\alpha_{2},\ldots,\alpha_{n-1}\alpha_n,\alpha_n\alpha_1$
belongs to I. Let
$\alpha_{1}\alpha_{2},\ldots,\alpha_{n-1}\alpha_n,\alpha_n\alpha_1$
belongs to I. Let
![]() $\mathcal C(\Lambda)$
be the set of cyclical permutation equivalence classes of saturated cycles without repeated arrows. For
$\mathcal C(\Lambda)$
be the set of cyclical permutation equivalence classes of saturated cycles without repeated arrows. For
![]() $n>2$
denote by
$n>2$
denote by
![]() $\mathcal D^b(K-mod)/\left[n\right]$
the triangulated orbit category as defined in [Reference Keller28]. Then [Reference Kalck27, Theorem 2.5] shows that
$\mathcal D^b(K-mod)/\left[n\right]$
the triangulated orbit category as defined in [Reference Keller28]. Then [Reference Kalck27, Theorem 2.5] shows that
![]() $\mathcal D_{sg}(\Lambda)$
and
$\mathcal D_{sg}(\Lambda)$
and
![]() $\prod_{c\in \mathcal C(\Lambda)} \mathcal D^b(K-mod)/\left[n_c\right]$
are equivalent as triangulated categories, where
$\prod_{c\in \mathcal C(\Lambda)} \mathcal D^b(K-mod)/\left[n_c\right]$
are equivalent as triangulated categories, where
![]() $n_c$
denotes the length of any cycle in the equivalence class
$n_c$
denotes the length of any cycle in the equivalence class
![]() $c\in \mathcal C(\Lambda)$
.
$c\in \mathcal C(\Lambda)$
.
By construction of the dual ribbon graph
![]() $G_\Lambda$
of a gentle algebra
$G_\Lambda$
of a gentle algebra
![]() $\Lambda$
, it is easy to see that there is a bijection between
$\Lambda$
, it is easy to see that there is a bijection between
![]() $\mathcal C(\Lambda)$
and the polygons in
$\mathcal C(\Lambda)$
and the polygons in
![]() $G_\Lambda$
with no boundary edges. We will call such polygons interior polygons and we denote by
$G_\Lambda$
with no boundary edges. We will call such polygons interior polygons and we denote by
![]() $\mathcal{P}^\circ_\Lambda$
the set of interior polygons. Furthermore, for
$\mathcal{P}^\circ_\Lambda$
the set of interior polygons. Furthermore, for
![]() $P \in \mathcal{P}^\circ_\Lambda$
denote by
$P \in \mathcal{P}^\circ_\Lambda$
denote by
![]() $n_P$
the number of edges of P. A concrete description of
$n_P$
the number of edges of P. A concrete description of
![]() $\mathcal D_{sg}(\Lambda)$
is then given by
$\mathcal D_{sg}(\Lambda)$
is then given by
The geometric description of the singularity category of a skew-gentle algebra follows from the fact that, by [Reference Chen and Lu14, Theorem 3.5], a skew-gentle algebra A and its underlying gentle algebra
![]() $\Lambda$
have equivalent singularity categories and that the generalised ribbon graph of a skew-gentle algebra and that of a gentle algebra have the same number of interior polygons and corresponding interior polygons have the same number of edges. More precisely, we have the following.
$\Lambda$
have equivalent singularity categories and that the generalised ribbon graph of a skew-gentle algebra and that of a gentle algebra have the same number of interior polygons and corresponding interior polygons have the same number of edges. More precisely, we have the following.
Theorem 7.1 Let A be a skew-gentle algebra and
![]() $(S, M, \mathcal{O}, G)$
be the orbifold dissection induced by the generalised ribbon graph G of A. Then
$(S, M, \mathcal{O}, G)$
be the orbifold dissection induced by the generalised ribbon graph G of A. Then
where
![]() $\mathcal{P}^\circ_A$
is the set of interior polygons of G and
$\mathcal{P}^\circ_A$
is the set of interior polygons of G and
![]() $n_P$
is the number of edges of P, for
$n_P$
is the number of edges of P, for
![]() $P \in \mathcal{\mathcal{P}^\circ_A }$
.
$P \in \mathcal{\mathcal{P}^\circ_A }$
.
7.2 Gorenstein dimension of skew-gentle algebras
Recall that a finite dimensional algebra A is d-Gorenstein if it has a finite injective dimension d as a left and right A-module. Both gentle and skew-gentle algebras are Gorenstein [Reference Geiß and Reiten18].
The following result shows that the Gorenstein dimension of a skew-gentle algebra can be read from its orbifold dissection. For this, we recall that a skew-gentle algebra gives rise to an orbifold dissection into generalised polygons which either have no boundary edges or which have exactly one boundary edge. We refer to the latter as a boundary polygon.
Theorem 7.2 Let A be a skew-gentle algebra and
![]() $(S, M, \mathcal{O}, G)$
be the orbifold dissection given by the generalised ribbon graph G of A. Then the Gorenstein dimension of A is equal to d, where
$(S, M, \mathcal{O}, G)$
be the orbifold dissection given by the generalised ribbon graph G of A. Then the Gorenstein dimension of A is equal to d, where
![]() $d-1$
is the maximal number of internal edges of boundary polygons of the dissection, if such boundary polygons exist or zero otherwise.
$d-1$
is the maximal number of internal edges of boundary polygons of the dissection, if such boundary polygons exist or zero otherwise.
Proof. Let
![]() $\Lambda$
be the gentle algebra obtained from A by deleting all special loops. By [Reference Geiß and de la Peña16], there exists a gentle algebra B such that A is Morita equivalent to the skew-group algebra
$\Lambda$
be the gentle algebra obtained from A by deleting all special loops. By [Reference Geiß and de la Peña16], there exists a gentle algebra B such that A is Morita equivalent to the skew-group algebra
![]() $B*\mathbb{Z}/2$
. Then by [Reference Auslander and Reiten4, Theorem 2.3] and [Reference Geiß and Reiten18], B is Gorenstein and the Gorenstein dimensions of B and A coincide.
$B*\mathbb{Z}/2$
. Then by [Reference Auslander and Reiten4, Theorem 2.3] and [Reference Geiß and Reiten18], B is Gorenstein and the Gorenstein dimensions of B and A coincide.
By [Reference Geiß and Reiten18], the Gorenstein dimension of
![]() $\Lambda$
is equal to the maximal length of saturated paths in A which are not cycles, if such paths exist or zero otherwise. The result follows from the properties of G.
$\Lambda$
is equal to the maximal length of saturated paths in A which are not cycles, if such paths exist or zero otherwise. The result follows from the properties of G.
7.3 q-Cartan matrices
A classical invariant for graded algebras is the so-called q-Cartan matrix which generalises the classical Cartan matrix of a graded finite dimensional algebra, see for example [Reference Fuller15]. For this, recall that
![]() $A=KQ/I$
has a grading induced by paths length if I is generated by homogeneous relations. The q-Cartan matrix
$A=KQ/I$
has a grading induced by paths length if I is generated by homogeneous relations. The q-Cartan matrix
![]() $C_A(q)=(c_{ij}(q))$
of A, for an indeterminate q, is the matrix with entries
$C_A(q)=(c_{ij}(q))$
of A, for an indeterminate q, is the matrix with entries
for vertices i, j in Q and where
![]() $(e_iAe_j)_n$
is the component of degree n of
$(e_iAe_j)_n$
is the component of degree n of
![]() $e_iAe_j$
. The q-Cartan matrix is invariant under graded derived equivalence and specialises to the classical Cartan matrix by setting
$e_iAe_j$
. The q-Cartan matrix is invariant under graded derived equivalence and specialises to the classical Cartan matrix by setting
![]() $q=1$
.
$q=1$
.
In [Reference Bessenrodt and Holm7, Theorem 4.2], the determinant of the q-Cartan matrix
![]() $C_A(q)$
of a (skew-)gentle algebra A is computed in terms of saturated cycles. In the following we show that this description can be read-off the orbifold dissection of A.
$C_A(q)$
of a (skew-)gentle algebra A is computed in terms of saturated cycles. In the following we show that this description can be read-off the orbifold dissection of A.
Theorem 7.3 Let A be a skew-gentle algebra and
![]() $(S, M, \mathcal{O}, G)$
be the orbifold dissection induced by the generalised ribbon graph
$(S, M, \mathcal{O}, G)$
be the orbifold dissection induced by the generalised ribbon graph
![]() $G_A$
of A. Denote by
$G_A$
of A. Denote by
![]() $c_k$
the number of (degenerate) interior polygons of G with k edges and let
$c_k$
the number of (degenerate) interior polygons of G with k edges and let
![]() $\Lambda$
be the gentle algebra obtained from A by deleting the special loops. Then the q-Cartan matrix
$\Lambda$
be the gentle algebra obtained from A by deleting the special loops. Then the q-Cartan matrix
![]() $C_A(q)$
has determinant
$C_A(q)$
has determinant
8. Example
In this section, we will illustrate the geometric model and some of the results in the previous sections on an example. Let
![]() $A=KQ/I$
be the skew-gentle algebra with admissible presentation
$A=KQ/I$
be the skew-gentle algebra with admissible presentation
![]() $A^{sg}=KQ^{sg}/I^{sg}$
, where Q and
$A^{sg}=KQ^{sg}/I^{sg}$
, where Q and
![]() $Q^{sg}$
are as follows
$Q^{sg}$
are as follows
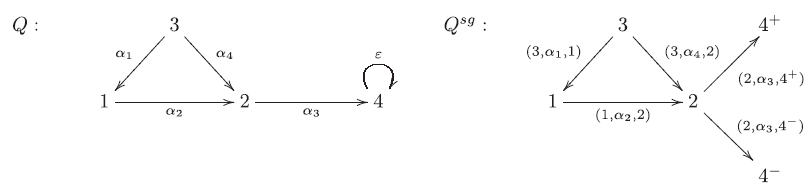
and where
![]() $I=\langle \alpha_1\alpha_2, \alpha_4\alpha_3, \varepsilon^2-\varepsilon\rangle$
and
$I=\langle \alpha_1\alpha_2, \alpha_4\alpha_3, \varepsilon^2-\varepsilon\rangle$
and
![]() $I^{sg}=\langle (3,\alpha_1, 1)(1,\alpha_2,2), (3,\alpha_4, 2)(2,\alpha_3 4^+), (3,\alpha_4, 2)(2,\alpha_3 4^-)\rangle$
.
$I^{sg}=\langle (3,\alpha_1, 1)(1,\alpha_2,2), (3,\alpha_4, 2)(2,\alpha_3 4^+), (3,\alpha_4, 2)(2,\alpha_3 4^-)\rangle$
.
Following Remark 3.4, the set of vertices
![]() $M_A$
of the ribbon graph is the set
$M_A$
of the ribbon graph is the set
![]() $\{\alpha_2\alpha_3\epsilon, \alpha_1,\alpha_4, e_4\}$
and its generalised ribbon graph
$\{\alpha_2\alpha_3\epsilon, \alpha_1,\alpha_4, e_4\}$
and its generalised ribbon graph
![]() $G_A$
can be seen in Figure 12. Note that the only difference between a ribbon graph and a generalised ribbon graph is that in a generalised ribbon graph some of the (leaf) vertices, namely those giving rise to orbifold points, are designated to be special.
$G_A$
can be seen in Figure 12. Note that the only difference between a ribbon graph and a generalised ribbon graph is that in a generalised ribbon graph some of the (leaf) vertices, namely those giving rise to orbifold points, are designated to be special.

Figure 12. Generalised ribbon graphs of algebra A.
Since A is a skew-gentle algebra, the generalised ribbon graph
![]() $G_A$
is embedded in an orbifold with one orbifold point of order 2 which corresponds to the special vertex
$G_A$
is embedded in an orbifold with one orbifold point of order 2 which corresponds to the special vertex
![]() $e_4$
. The corresponding orbifold dissection of A and its dual graph are depicted in Figure 13.
$e_4$
. The corresponding orbifold dissection of A and its dual graph are depicted in Figure 13.

Figure 13. Orbifold dissection induced by
![]() $G_A$
and its dual graph.
$G_A$
and its dual graph.
Let
![]() $(\gamma, f)$
be the graded curve where
$(\gamma, f)$
be the graded curve where
![]() $\gamma$
is as in Figure 14 and where the grading is given by
$\gamma$
is as in Figure 14 and where the grading is given by
![]() $f=(1,2,1,0)$
. The homotopy string
$f=(1,2,1,0)$
. The homotopy string
![]() $\sigma(\gamma)$
associated with
$\sigma(\gamma)$
associated with
![]() $\gamma$
is
$\gamma$
is
![]() $(\alpha_2\alpha_3)(\overline{\alpha_3})(\overline{\alpha_4})$
and the grading
$(\alpha_2\alpha_3)(\overline{\alpha_3})(\overline{\alpha_4})$
and the grading
![]() $\mu(f)$
induced by f. This induces the following asymmetric string complex
$\mu(f)$
induced by f. This induces the following asymmetric string complex
![]() $P^\bullet_{(\sigma(\gamma), \mu(f))}$
in
$P^\bullet_{(\sigma(\gamma), \mu(f))}$
in
![]() $K^{b,-}(proj-A^{sg})$
.
$K^{b,-}(proj-A^{sg})$
.


Figure 14. The curves
![]() $\gamma$
and
$\gamma$
and
![]() $\delta$
in the orbifold dissection
$\delta$
in the orbifold dissection
![]() $(S,M, \mathcal{O}, G_A).$
$(S,M, \mathcal{O}, G_A).$
Let
![]() $(\delta, g)$
be the graded closed curve where
$(\delta, g)$
be the graded closed curve where
![]() $\delta$
is depicted in Figure 14 and
$\delta$
is depicted in Figure 14 and
![]() $g=(0,1,0,-1,0)$
. The asymmetric homotopy band
$g=(0,1,0,-1,0)$
. The asymmetric homotopy band
![]() $\sigma(\delta)$
associated with
$\sigma(\delta)$
associated with
![]() $\delta$
is
$\delta$
is
![]() $(\alpha_2\alpha_3)(\overline{\alpha_3})(\overline{\alpha_4})(\alpha_1)$
and as before
$(\alpha_2\alpha_3)(\overline{\alpha_3})(\overline{\alpha_4})(\alpha_1)$
and as before
![]() $\mu(g)$
is induced by g. Let
$\mu(g)$
is induced by g. Let
![]() $q(x)\in \operatorname{ind} K[x]$
be a non-trivial power of an irreducible polynomial over K with leading coefficient equal to 1 and different from x and
$q(x)\in \operatorname{ind} K[x]$
be a non-trivial power of an irreducible polynomial over K with leading coefficient equal to 1 and different from x and
![]() $x-1$
. The asymmetric band complex
$x-1$
. The asymmetric band complex
![]() $P^\bullet_{(\sigma(\delta), \mu(g), p(x))}$
in
$P^\bullet_{(\sigma(\delta), \mu(g), p(x))}$
in
![]() $K^{b,-}(proj A^{sg})$
induced by
$K^{b,-}(proj A^{sg})$
induced by
![]() $(\sigma(\delta), \mu(g))$
is
$(\sigma(\delta), \mu(g))$
is
where
![]() $P(i)=P_i$
for
$P(i)=P_i$
for
![]() $i\neq 4$
and
$i\neq 4$
and
![]() $P(4)=P_{4^+}\oplus P_{4^-}$
.
$P(4)=P_{4^+}\oplus P_{4^-}$
.
Observe that the set of interior polygons of G is empty. Thus by Theorem 7.1, the singularity category
![]() $\mathcal D_{sg}(A)$
is equivalent to the category with one element, and by Theorem 7.3, the determinant
$\mathcal D_{sg}(A)$
is equivalent to the category with one element, and by Theorem 7.3, the determinant
![]() $\operatorname{det}C_A(q)$
of the q-Cartan matrix
$\operatorname{det}C_A(q)$
of the q-Cartan matrix
![]() $C_A(q)$
is zero.
$C_A(q)$
is zero.
By 7.2, to compute the Gorenstein dimension of A, we need to count the maximal number d of internal edges of boundary polygons of the dissection, in this case, the dissection has one digon and two 4-gon, then
![]() $d=3$
, and as a consequence, the Gorenstein dimension of A is
$d=3$
, and as a consequence, the Gorenstein dimension of A is
![]() $3-1=2$
.
$3-1=2$
.
Acknowledgements
The authors would like to thank Claire Amiot and Thomas Brüstle for discussing and sharing the results of their recent paper [Reference Amiot and Brüstle1] while both their and our papers were still in preparation. The authors would also like to particularly thank Viktor Bekkert and Eduardo Marcos for helpful conversations in relation to [Reference Bekkert, Marcos and Merklen5].



































