Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T22:35:32.358Z Has data issue: false hasContentIssue false
  • English
  • Français

Curves with zero derivative in F-spaces

Published online by Cambridge University Press:  18 May 2009

N. J. Kalton
N. J. Kalton
Affiliation:
Department of Mathematics, University of Missouri-Columbia, Columbia Missouri 65211, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be an F-space (complete metric linear space) and suppose g:[0, 1] → X is a continuous map. Suppose that g has zero derivative on [0, 1], i.e.

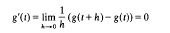
for 0≤t≤1 (we take the left and right derivatives at the end points). Then, if X is locally convex or even if it merely possesses a separating family of continuous linear functionals, we can conclude that g is constant by using the Mean Value Theorem. If however X* = {0} then it may happen that g is not constant; for example, let X = Lp(0, 1) (0≤p≤1) and g(t) = l[0,t] (0≤t≤1) (the characteristic function of [0, t]). This example is due to Rolewicz [6], [7; p. 116].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 22 , Issue 1 , January 1981 , pp. 19 - 29
Copyright
Copyright © Glasgow Mathematical Journal Trust 1981

References

REFERENCES

1.Bessaga, C., Pelczyński, A. and Rolewicz, S., Some properties of the norm in F-spaces, Studia Math. 16 (1957), 183–192.CrossRefGoogle Scholar
2.Kalton, N. J., An F-space with trivial dual where the Krein-Milman theorem holds, Israel J. Math. 36 (1980), 41–50.CrossRefGoogle Scholar
3.Ribe, M., On the separation properties of the duals of general topological vector spaces, Ark. Mat. 9 (1971), 279–302.Google Scholar
4.Roberts, J. W., A compact convex set with no extreme points. Studia Math. 60 (1977), 255–266.Google Scholar
5.Roberts, J. W., Pathological compact convex sets in the spaces L p, O≤p≤l, The Altgeld Book (University of Illinois, 1976).Google Scholar
6.Rolewicz, S., O funkcjach o pochodnej zero, Wiadom. Math. (2) 3 (1959), 127–128.Google Scholar
7.Rolewicz, S., Metric linear spaces (PWN Warsaw, 1972).Google Scholar
8.Turpin, P., Convexités dans les espaces vectoriels topologiques généraux, Dissertationes Math. (Rozprawy Mat.) 131 (1976).Google Scholar