Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-22T01:58:19.787Z Has data issue: false hasContentIssue false
  • English
  • Français

A CRITERION FOR THE JACOBSON SEMISIMPLICITY OF THE GREEN RING OF A FINITE TENSOR CATEGORY

Part of: Categories with structure Hopf algebras, quantum groups and related topics Representation theory of rings and algebras

Published online by Cambridge University Press:  25 September 2017

ZHIHUA WANG ,
LIBIN LI  and
YINHUO ZHANG
ZHIHUA WANG
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, China Department of Mathematics, Taizhou University, Taizhou 225300, China e-mail: [email protected]
LIBIN LI
Affiliation:
School of Mathematical Science, Yangzhou University, Yangzhou 225002, China e-mail: [email protected]
YINHUO ZHANG
Affiliation:
Department of Mathematics and Statistics, University of Hasselt, Universitaire Campus, 3590 Diepeenbeek, Belgium e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper deals with the Green ring 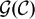$\mathcal{G}(\mathcal{C})$ of a finite tensor category 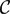$\mathcal{C}$ with finitely many isomorphism classes of indecomposable objects over an algebraically closed field. The first part of this paper deals with the question of when the Green ring 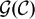$\mathcal{G}(\mathcal{C})$, or the Green algebra 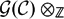$\mathcal{G}(\mathcal{C})\otimes_{\mathbb {Z}}$K over a field K, is Jacobson semisimple (namely, has zero Jacobson radical). It turns out that 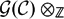$\mathcal{G}(\mathcal{C})\otimes_{\mathbb {Z}}$K is Jacobson semisimple if and only if the Casimir number of 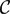$\mathcal{C}$ is not zero in K. For the Green ring 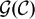$\mathcal{G}(\mathcal{C})$ itself, 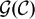$\mathcal{G}(\mathcal{C})$ is Jacobson semisimple if and only if the Casimir number of 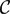$\mathcal{C}$ is not zero. The second part of this paper focuses on the case where 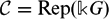$\mathcal{C}=\text{Rep}(\mathbb {k}G)$ for a cyclic group G of order p over a field 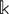$\mathbb {k}$ of characteristic p. In this case, the Casimir number of 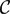$\mathcal{C}$ is computable and is shown to be 2p2. This leads to a complete description of the Jacobson radical of the Green algebra 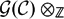$\mathcal{G}(\mathcal{C})\otimes_{\mathbb {Z}}$K over any field K.

MSC classification

Primary: 16G70: Auslander-Reiten sequences (almost split sequences) and Auslander-Reiten quivers
Secondary: 16T05: Hopf algebras and their applications 18D10: Monoidal categories (= multiplicative categories), symmetric monoidal categories, braided categories
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 60 , Issue 1 , January 2018 , pp. 253 - 272
Copyright
Copyright © Glasgow Mathematical Journal Trust 2017 

References

REFERENCES

1. Auslander, M., Reiten, I. and Smalø, S. O., Representation theory of Artin algebras, vol. 36 (Cambridge Studies in Advanced Mathematics, Cambridge, 1994).Google Scholar
2. Bakalov, B. and Kirillov, A. A., Lectures on tensor categories and modular functors, vol. 21, (AMS, Providence, 2001).Google Scholar
3. Benson, D. J., The Green ring of a finite group, J. Algebra 87 (1984), 290–331.Google Scholar
4. Benson, D. J. and Carlson, J. F., Nilpotent elements in the Green ring, J. Algebra 104 (1986), 329–350.CrossRefGoogle Scholar
5. Bhargava, M. and Zieve, M. E., Factoring Dickson polynomials over finite fields, Finite Fields Appl. 5 (2) (1999), 103–111.Google Scholar
6. Chen, H., The green ring of drinfeld double D(H 4), Algebras and Representation Theory 17 (5) (2014), 1457–1483.Google Scholar
7. Chen, H., Oystaeyen, F. V. and Zhang, Y., The green rings of taft algebras, Proc. Amer. Math. Soc. 142 (2014), 765–775.Google Scholar
8. Chou, W. S., The factorization of Dickson polynomials over finite fields, Finite Fields Appl. 3 (1997), 84–96.CrossRefGoogle Scholar
9. Darpö, E. and Herschend, M., On the representation ring of the polynomial algebra over perfect field, Math. Z 265 (2011), 605–615.Google Scholar
10. Domokos, M. and Lenagan, T. H., Representation rings of quantum groups, J. Algebra 282 (2004), 103–128.Google Scholar
11. Etingof, P., Gelaki, S., Nikshych, D. and Ostrik, V., Tensor categories, Mathematical Surveys and Monographs, vol. 205 (AMS, Providence, RI, 2015).Google Scholar
12. Etingof, P. and Ostrik, V., Finite tensor categories, Mosc. Math. J 4 (3) (2004), 627–654.CrossRefGoogle Scholar
13. Green, J. A., A transfer theorem for modular representations, J. Algebra 1 (1964), 73–84.Google Scholar
14. Green, J. A., The modular representation algebra of a finite group, Ill. J. Math. 6 (4) (1962), 607–619.Google Scholar
15. Higman, D. G., On orders in separable algebras, Canad. J. Math. 7 (1955), 509–515.Google Scholar
16. Huang, H., Oystaeyen, F. V., Yang, Y. and Zhang, Y., The Green rings of pointed tensor categories of finite type, J. Pure Appl. Algebra 218 (2014), 333–342.Google Scholar
17. Li, Y. and Hu, N., The Green rings of the 2-rank Taft algebra and its two relatives twisted, J. Algebra 410 (2014), 1–35.Google Scholar
18. Li, L. and Zhang, Y., The Green rings of the generalized Taft Hopf algebras, Contemp. Math. 585 (2013), 275–288.Google Scholar
19. Liu, S., Auslander-Reiten theory in a Krull-Schmidt category, São Paulo J. Math. Sci. 4 (3) (2010), 425–472.Google Scholar
20. Lorenz, M., Some applications of Frobenius algebras to Hopf algebras, Contemp. Math. 537 (2011), 269–289.Google Scholar
21. McDonald, B. R., Finite rings with identity, vol. 28 (Marcel Dekker Incorporated, 1974).Google Scholar
22. Ringel, C. M., Tame algebras and integral quadratic forms, Lecture Notes in Mathematics, vol. 1099 (Springer, Berlin Heidelberg, 1984).CrossRefGoogle Scholar
23. Wang, Z., Li, L. and Zhang, Y., Green rings of pointed rank one Hopf algebras of nilpotent type, Algebras Represent. Theory 17 (6) (2014), 1901–1924.Google Scholar
24. Wang, Z., Li, L. and Zhang, Y., Green rings of pointed rank one Hopf algebras of non-nilpotent type, J. Algebra 449 (2016), 108–137.CrossRefGoogle Scholar
25. Witherspoon, S. J., The representation ring of the quantum double of a finite group, J. Algebra 179 (1996), 305–329.CrossRefGoogle Scholar
26. Zemanek, J., Nilpotent elements in representation rings, J. Algebra 19 (1971), 453–469.Google Scholar