Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T07:46:16.989Z Has data issue: false hasContentIssue false
  • English
  • Français

COVERS FOR S-ACTS AND CONDITION (A) FOR A MONOID S

Part of: Semigroups

Published online by Cambridge University Press:  19 December 2014

ALEX BAILEY ,
VICTORIA GOULD ,
MIKLÓS HARTMANN ,
JAMES RENSHAW  and
LUBNA SHAHEEN
ALEX BAILEY
Affiliation:
School of Mathematics, University of Southampton, Highfield Southampton SO17 1BJ, United Kingdom e-mail: [email protected]
VICTORIA GOULD
Affiliation:
Department of Mathematics, University of York, Heslington, York YO10 5DD, United Kingdom e-mail: [email protected]
MIKLÓS HARTMANN
Affiliation:
Department of Mathematics, University of York, Heslington, York YO10 5DD, United Kingdom e-mail: [email protected]
JAMES RENSHAW
Affiliation:
School of Mathematics, University of Southampton, Highfield, Southampton SO17, 1BJ, United Kingdom e-mail: [email protected]
LUBNA SHAHEEN
Affiliation:
Department of Mathematics, University of York, Heslington, York YO10 5DD, United Kingdom e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A monoid S satisfies Condition (A) if every locally cyclic left S-act is cyclic. This condition first arose in Isbell's work on left perfect monoids, that is, monoids such that every left S-act has a projective cover. Isbell showed that S is left perfect if and only if every cyclic left S-act has a projective cover and Condition (A) holds. Fountain built on Isbell's work to show that S is left perfect if and only if it satisfies Condition (A) together with the descending chain condition on principal right ideals, MR. We note that a ring is left perfect (with an analogous definition) if and only if it satisfies MR. The appearance of Condition (A) in this context is, therefore, monoid specific. Condition (A) has a number of alternative characterisations, in particular, it is equivalent to the ascending chain condition on cyclic subacts of any left S-act. In spite of this, it remains somewhat esoteric. The first aim of this paper is to investigate the preservation of Condition (A) under basic semigroup-theoretic constructions. Recently, Khosravi, Ershad and Sedaghatjoo have shown that every left S-act has a strongly flat or Condition (P) cover if and only if every cyclic left S-act has such a cover and Condition (A) holds. Here we find a range of classes of S-acts 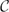$\mathcal{C}$ such that every left S-act has a cover from 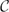$\mathcal{C}$ if and only if every cyclic left S-act does and Condition (A) holds. In doing so we find a further characterisation of Condition (A) purely in terms of the existence of covers of a certain kind. Finally, we make some observations concerning left perfect monoids and investigate a class of monoids close to being left perfect, which we name left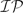$\mathcal{IP}$a-perfect.

MSC classification

Primary: 20M30: Representation of semigroups; actions of semigroups on sets
Secondary: 20M50: Connections of semigroups with homological algebra and category theory
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 57 , Issue 2 , May 2015 , pp. 323 - 341
Copyright
Copyright © Glasgow Mathematical Journal Trust 2014 

References

REFERENCES

1.Bailey, A. and Renshaw, J., Covers of acts over monoids and pure epimorphisms, to appear in Proc. Edinburgh Math. Soc.Google Scholar
2.Fountain, J. B., Perfect semigroups, Proc. Edinburgh Math. Soc. 20 (1976), 87–93.Google Scholar
3.Gould, V. and Shaheen, L., Perfection for pomonoids Semigroup Forum 81 (2010), 102–127.CrossRefGoogle Scholar
4.Khosravi, R., Ershad, M. and Sedaghatjoo, M., Strongly flat and condition (P) covers of acts over monoids, Comm. Algebra 38 (2010), 4520–4530.CrossRefGoogle Scholar
5.Isbell, J. R., Perfect monoids Semigroup Forum 2 (1971), 95–118.Google Scholar
6.Kilp, M., On monoids over which all strongly flat cyclic right acts are projective Semigroup Forum 52 (1996), 241–245.CrossRefGoogle Scholar
7.Kilp, M., Knauer, U. and Mikhalev, A. V., Monoids, Acts, and Categories, (de Gruyter, Berlin 2000).CrossRefGoogle Scholar
8.Kilp, M. and Laan, V., On flatness properties of cyclic acts Comm. Algebra 28 (2000), 2919–2926.Google Scholar
9.Knauer, U., Projectivity of acts and Morita equivalence of monoids Semigroup Forum 3 (1972), 359–370.Google Scholar
10.Mahmoudi, M. and Renshaw, J., On covers of cyclic acts over monoids Semigroup Forum 77 (2008), 325–338.Google Scholar
11.Qiao, H. and Wang, L., On flatness covers of cyclic acts over monoids Glasg. Math. J. 54 (2012), 163–167.Google Scholar
12.Renshaw, J., Monoids for which condition (P) acts are projective, Semigroup Forum 61 (2000), 46–56.Google Scholar