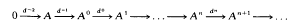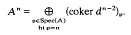Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gibson, G.J.
and
O'Carroll, L.
1988.
Direct limit systems, generalized fractions and complexes of cousin type.
Journal of Pure and Applied Algebra,
Vol. 54,
Issue. 2-3,
p.
249.
Sharp, R. Y.
and
Yassi, M.
1990.
Generalized fractions and Hughes' gradetheoretic analogue of the Cousin complex.
Glasgow Mathematical Journal,
Vol. 32,
Issue. 2,
p.
173.
Chung, Sang-Cho
1994.
Complexes of Cousin type and modules of generalized fractions.
Nagoya Mathematical Journal,
Vol. 136,
Issue. ,
p.
17.
Khashyarmanesh, Kazem
2009.
Gorenstein Injective Resolutions, Cousin Complexes and Top Local Cohomology Modules.
Algebra Colloquium,
Vol. 16,
Issue. 01,
p.
95.
Bamdad, Hamidreza
and
Vahidi, Alireza
2018.
Extension Functors of Cousin Cohomology Modules.
Bulletin of the Iranian Mathematical Society,
Vol. 44,
Issue. 2,
p.
253.