No CrossRef data available.
Article contents
CO-UNIVERSAL C*-ALGEBRAS ASSOCIATED TO APERIODIC k-GRAPHS
Published online by Cambridge University Press: 13 August 2013
Abstract
We construct a representation of each finitely aligned aperiodic k-graph Λ on the Hilbert space 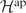 $\mathcal{H}^{\rm ap}$ with basis indexed by aperiodic boundary paths in Λ. We show that the canonical expectation on
$\mathcal{H}^{\rm ap}$ with basis indexed by aperiodic boundary paths in Λ. We show that the canonical expectation on 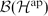 $\mathcal{B}(\mathcal{H}^{\rm ap})$ restricts to an expectation of the image of this representation onto the subalgebra spanned by the final projections of the generating partial isometries. We then show that every quotient of the Toeplitz algebra of the k-graph admits an expectation compatible with this one. Using this, we prove that the image of our representation, which is canonically isomorphic to the Cuntz–Krieger algebra, is co-universal for Toeplitz–Cuntz–Krieger families consisting of non-zero partial isometries.
$\mathcal{B}(\mathcal{H}^{\rm ap})$ restricts to an expectation of the image of this representation onto the subalgebra spanned by the final projections of the generating partial isometries. We then show that every quotient of the Toeplitz algebra of the k-graph admits an expectation compatible with this one. Using this, we prove that the image of our representation, which is canonically isomorphic to the Cuntz–Krieger algebra, is co-universal for Toeplitz–Cuntz–Krieger families consisting of non-zero partial isometries.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2013


