Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T17:15:44.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Coordinates for analytic operator algebras

Published online by Cambridge University Press:  18 May 2009

Baruch Solel
Baruch Solel
Affiliation:
Department of Mathematics and Computing Science, University of Haifa, Haifa 31999, Israel
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be a σ-finite von Neumann algebra and α = {αt}t∈A be a representation of a compact abelian group A as *-automorphisms of M. Let Γ be the dual group of A and suppose that Γ is totally ordered with a positive semigroup Σ⊆Γ. The analytic algebra associated with α and Σ is

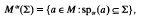
where spα(a) is Arveson's spectrum. These algebras were studied (also for A not necessarily compact) by several authors starting with Loebl and Muhly [10].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 31 , Issue 1 , January 1989 , pp. 31 - 47
Copyright
Copyright © Glasgow Mathematical Journal Trust 1989

References

1.Arveson, W., Analyticity in operator algebras, Amer. J. Math. 89 (1967), 578–642.CrossRefGoogle Scholar
2.Feldman, J. and Moore, C. C., Ergodic equivalence relations, cohomology and von Neumann algebras I, Trans. Amer. Math. Soc. 234 (1977), 289–324.CrossRefGoogle Scholar
3.Hahn, P., Haar measure for measured groupoids, Trans. Amer. Math. Soc. 242 (1978), 1–33.Google Scholar
4.Ikunishi, A. and Nakagami, Y., On invariants G(σ) and Γ(σ) for an automorphism group of a von Neumann algebra. Publ. Res. Inst. Math. Sci. 12 (1976), 1–30.CrossRefGoogle Scholar
5.Kadison, R. V. and Ringrose, J. R., Fundamentals of the theory of operator algebras, Vol. II (Academic Press, 1986).Google Scholar
6.Kraus, J., Compact abelian groups of automorphisms of von Neumann algebras, J. Functional Analysis 39 (1980), 347–374.CrossRefGoogle Scholar
7.Kraus, J., W*-dynamical systems and reflexive operator algebras. J. Operator Theory 8 (1982), 181–194.Google Scholar
8.Larson, D. R. and Solel, B., Nests and inner flows. J. Operator Theory 16 (1986), 157–164.Google Scholar
9.Loginov, A. and Sulman, V., Hereditary and intermediate reflexivity of W*-algebras. Math. USSR Izv 9 (1975), 1189–1201.CrossRefGoogle Scholar
10.Loebl, R. and Muhly, P. S., Analyticity and flows in von Neumann algebras, J. Functional Analysis 29 (1978), 214–252.CrossRefGoogle Scholar
11.Muhly, P. S. and Saito, K.-S., Analytic crossed products and outer conjugacy classes of automorphisms of von Neumann algebras. Math. Scand. 58 (1986), 55–68.CrossRefGoogle Scholar
12.Muhly, P. S. and Saito, K.-S., Analytic crossed products and outer conjugacy classes of automorphisms of von Neumann algebras II, Preprint.Google Scholar
13.Muhly, P. S., Saito, K.-S. and Solel, B., Coordinates for triangular operator algebras, Preprint.Google Scholar
14.Ramsay, A., Virtual groups and group action, Advances in Math. 6 (1971), 253–322.CrossRefGoogle Scholar
15.Schmidt, K., Lectures on cocycles of ergodic transformation groups (Macmillan, 1980).Google Scholar
16.Solel, B., Invariant subspaces for algebras of analytic operators associated with a periodic flow on a finite von Neumann algebra, J. Functional Analysis 58 (1984), 1–19.CrossRefGoogle Scholar
17.Solel, B., Algebras of analytic operators associated with a periodic flow on a von Neumann algebra. Canad. J. Math. 37 (1985), 405–429.CrossRefGoogle Scholar
18.Takesaki, M., Conditional expectations in von Neumann algebras. J. Functional Analysis 9 (1972), 306–321.CrossRefGoogle Scholar