No CrossRef data available.
Article contents
The connective 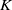 $K$-theory of the Eilenberg–MacLane space
$K$-theory of the Eilenberg–MacLane space 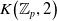 $K\!\left({\mathbb{Z}}_p,\textrm{2}\right)$
$K\!\left({\mathbb{Z}}_p,\textrm{2}\right)$
Published online by Cambridge University Press: 11 December 2023
Abstract
We compute 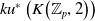 $ku^*\left(K\!\left({\mathbb{Z}}_p,2\right)\right)$ and
$ku^*\left(K\!\left({\mathbb{Z}}_p,2\right)\right)$ and 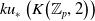 $ku_*\left(K\!\left({\mathbb{Z}}_p,2\right)\right)$, the connective
$ku_*\left(K\!\left({\mathbb{Z}}_p,2\right)\right)$, the connective 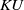 $KU$-cohomology and connective
$KU$-cohomology and connective 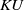 $KU$-homology groups of the mod-
$KU$-homology groups of the mod-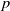 $p$ Eilenberg–MacLane space
$p$ Eilenberg–MacLane space 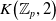 $K\!\left({\mathbb{Z}}_p,2\right)$, using the Adams spectral sequence. We obtain a striking interaction between
$K\!\left({\mathbb{Z}}_p,2\right)$, using the Adams spectral sequence. We obtain a striking interaction between 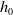 $h_0$-extensions and exotic extensions. The mod-
$h_0$-extensions and exotic extensions. The mod-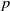 $p$ connective
$p$ connective 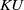 $KU$-cohomology groups, computed elsewhere, are needed in order to establish higher differentials and exotic extensions in the integral groups.
$KU$-cohomology groups, computed elsewhere, are needed in order to establish higher differentials and exotic extensions in the integral groups.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust



