Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T07:24:29.312Z Has data issue: false hasContentIssue false
  • English
  • Français

Components in vector lattices and extreme extensions of quasi-measures and measures

Published online by Cambridge University Press:  18 May 2009

Z. Lipecki
Z. Lipecki
Affiliation:
Institute of MathematicsPolish Academy of SciencesWroclaw BranchKopernika 1851–617 WroclawPoland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We develop some ideas contained in the author's paper [8] which was, in turn, inspired by Bierlein and Stich [5]. The main body of the present paper is divided into three sections. Section 2 is concerned with some vector-lattice-theoretical results. They are then applied to extensions of quasi-measures and measures in Sections 3 and 4, respectively.

Let X be a vector lattice, let x ε X+ and let S be a non-empty set. Theorems 1 and 2 describe some properties of the convex set

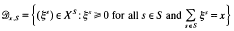
(see Section 2 for the definition of the sum above). The extreme points of Dx,s are characterized in terms of the components of x. It is also shown that if X has the principal projection property and S is countable, then extr Dx,s is, in some sense, large in Dx,s. Furthermore, for finite S, each point in Dx,s is then a sσ-convex combination of extreme ones.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 35 , Issue 2 , May 1993 , pp. 153 - 162
Copyright
Copyright © Glasgow Mathematical Journal Trust 1993

References

REFERENCES

1.Aliprantis, C. D. and Burkinshaw, O., Positive operators (Academic Press, 1985).Google Scholar
2.Ascherl, A. and Lehn, J., Two principles for extending probability measures, Manuscripta Math. 21 (1977), 43–50.CrossRefGoogle Scholar
3.Rao, K. P. S. Bhaskara and Rao, M. Bhaskara, Theory of charges. A study of finitely additive measures (Academic Press, 1983).Google Scholar
4.Bierlein, D., Über die Fortsetzung von Wahrscheinlichkeitsfeldern, Z. Wahrsch. Verw. Gebiete 1 (1962), 28–46.Google Scholar
5.Bierlein, D. and Stich, W. J. A., On the extremality of measure extensions, Manuscripta Math. 63 (1989), 89–97.CrossRefGoogle Scholar
6.Edwards, D. A., On a theorem of Dvoretsky, Wald, and Wolfowitz concerning Liapounov measures, Glasgow Math. J. 29 (1987), 205–220.CrossRefGoogle Scholar
7.Goller, H., An extension of Lyapounov's convexity theorem and (non-) randomization of tests, Statist. Decisions 2 (1984), 315–328.Google Scholar
8.Lipecki, Z., On extreme extensions of quasi-measures, Arch. Math. (Basel) 58 (1992), 288–293.CrossRefGoogle Scholar
9.Luxemburg, W. A. J. and Zaanen, A. C., Riesz spaces, Vol. I (North-Holland, 1971).Google Scholar
10.Nikodym, O., Sur les fonctions d'ensembles, in Comptes-Rendus du I Congrès des Mathématiciens des Pays Slaves, Warszawa 1929 (Warszawa 1930), 304–313.Google Scholar
11.Oates, D., A sequentially convex hull, Bull. London Math. Soc. 22 (1990), 467–468.CrossRefGoogle Scholar
12.Plachky, D., Extremal and monogenic additive set functions, Proc. Amer. Math. Soc. 54 (1976), 193–196.CrossRefGoogle Scholar
13.Weber, H., Ein Fortsetzungssatz für gruppenwertige Masse, Arch. Math. (Basel) 34 (1980), 157–159.Google Scholar