Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-05T02:27:53.223Z Has data issue: false hasContentIssue false
  • English
  • Français

Comparison theorems for the square integrability of solutions of (r(t)y')'+q(t)y=f(t, y)

Published online by Cambridge University Press:  18 May 2009

John S. Bradley
John S. Bradley
Affiliation:
University of Tennessee, Knoxville, Tennessee 37916
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Bellman [1], [2, p. 116] proved that, if all solutions of the equation

are in L2, ∞) and b(t) is bounded, then all solutions of

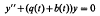
are also in L2(a, ∞). The purpose of this paper is to present conditions on the function f that guarantee that all solutions of

be in the class L2(a, ∞) whenever all solutions of the equation

have this property. It is assumed that r(t) >0, r and qare continuous on a half line (a, ∞) and f is continuous. Actually the continuity assumptions may be weakened to local integrability and L2 (a, ∞) may be replaced by Lp(a, ∞) for any p > 1.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 13 , Issue 1 , March 1972 , pp. 75 - 79
Copyright
Copyright © Glasgow Mathematical Journal Trust 1972

References

REFERENCES

1.Bellman, R., A stability property of solutions of linear differential equations, Duke Math. J. 11 (1944), 513–516.CrossRefGoogle Scholar
2.Bellman, R., Stability theory of differential equations (New York, 1953).Google Scholar
3.Gollwitzer, H. E., A note on a functional inequality, Proc. Amer. Math. Soc. 23 (1969), 642–647.CrossRefGoogle Scholar
4.Halvorsen, S., On the quadratic integrability of solutions of d'x/dt2+f(t)x =0, Math. Scand. 14 (1964), 111–119.CrossRefGoogle Scholar
5.Coddington, E. A. and Levinson, N., Theory of ordinary differential equations (New York, 1955).Google Scholar