Article contents
Compact actions on C*-algebras
Published online by Cambridge University Press: 18 May 2009
Extract
In Section 33 of [2], Bonsall and Duncan define an element t of a Banach algebra 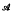 to act compactly on
to act compactly on 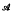 if the map a → tat is a compact operator on
if the map a → tat is a compact operator on 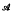 . In this paper, the arguments and technique of [1] are used to study this question for C*-algebras (see also [10]). We determine the elements b of a C*-algebra
. In this paper, the arguments and technique of [1] are used to study this question for C*-algebras (see also [10]). We determine the elements b of a C*-algebra 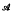 for which the maps a → ba, a → ab, a → ab + ba, a → bab are compact (respectively weakly compact), determine the C*-algebras which are compact in the sense of Definition 9, of [2, p. 177] and give a characterization of the C*-automorphisms of
for which the maps a → ba, a → ab, a → ab + ba, a → bab are compact (respectively weakly compact), determine the C*-algebras which are compact in the sense of Definition 9, of [2, p. 177] and give a characterization of the C*-automorphisms of 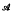 which are weakly compact perturbations of the identity.
which are weakly compact perturbations of the identity.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1980
References
REFERENCES
- 1
- Cited by


