Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-12T23:12:06.443Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact actions on C*-algebras

Published online by Cambridge University Press:  18 May 2009

Charles A. Akemann  and
Steve Wright
Charles A. Akemann
Affiliation:
University of California, Santa Barbara, California 93106
Steve Wright
Affiliation:
Oakland University, Rochester, Michigan 48063
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In Section 33 of [2], Bonsall and Duncan define an element t of a Banach algebra 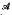to act compactly on 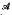if the map a → tat is a compact operator on 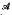. In this paper, the arguments and technique of [1] are used to study this question for C*-algebras (see also [10]). We determine the elements b of a C*-algebra 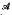for which the maps a→ba, a→ab, a→ab + ba, a→bab are compact (respectively weakly compact), determine the C*-algebras which are compact in the sense of Definition 9, of [2, p. 177] and give a characterization of the *-automorphisms of 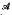which are weakly compact perturbations of the identity.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 21 , Issue 1 , January 1980 , pp. 143 - 149
Copyright
Copyright © Glasgow Mathematical Journal Trust 1980

References

REFERENCES

1.Akemann, C. A. and Wright, S., Compact and weakly compact derivations of C*-algebras, Pacific J. Math., to appear.Google Scholar
2.Bonsall, F. F. and Duncan, J., Complete normed algebras, Ergebnesse der Mathematik und ihrer Grenzgebiete, Bd. 80, (Springer-Verlag, 1973).CrossRefGoogle Scholar
3.Douglas, R. G., Banach algebra techniques in operator theory, (Academic Press, 1972).Google Scholar
4.Dunford, N. and Schwartz, J. T., Linear operators, Part I, (Interscience, 1958).Google Scholar
5.Glimm, J. and Kadison, R. V., Unitary operators in C*-algebras, Pacific J. Math., 10 (1960), 547–556.CrossRefGoogle Scholar
6.Kadison, R. V. and Ringrose, J. R., Derivations and automorphisms of operator algebras, Comm. Math. Phys., 4 (1967), 32–63.CrossRefGoogle Scholar
7.Ogasawara, T. and Yoshinaga, K., Weakly completely continuous Banach *-algebras, J. Sci. Hiroshima Univ., Ser. A, 18 (1954), 15–36.Google Scholar
8.Sakai, S., Weakly compact operators on operator algebras, Pacific J. Math., 14 (1964), 659–664.CrossRefGoogle Scholar
9.Sakai, S., C*-algebras and W*-algebras, Ergebnesse der Mathematik und ihrer Grenzgebiete, Bd. 60, (Springer-Verlag, 1971).Google Scholar
10.Tomiuk, B. J., Duality and the existence of weakly completely continuous elements in a B*-algebra, Glasgow Math. J., 13 (1972), 56–60.CrossRefGoogle Scholar
11.Vala, K., On compact sets of compact operators, Ann. Acad. Sci. Fenn., Ser. Al, 407 (1967).Google Scholar