Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T07:36:30.116Z Has data issue: false hasContentIssue false
  • English
  • Français

COMMON FIXED POINTS OF A PAIR OF NON-EXPANSIVE MAPPINGS WITH APPLICATIONS TO CONVEX FEASIBILITY PROBLEMS

Published online by Cambridge University Press:  25 November 2009

XIAOLONG QIN ,
SUN YOUNG CHO  and
HAIYUN ZHOU
XIAOLONG QIN*
Affiliation:
Department of Mathematics, Gyeongsang National University, Chinju 660-701, Korea e-mails: [email protected], [email protected]
SUN YOUNG CHO
Affiliation:
Department of Mathematics, Gyeongsang National University, Chinju 660-701, Korea e-mails: [email protected], [email protected]
HAIYUN ZHOU
Affiliation:
Department of Mathematics, Shijiazhuang Mechanical Engineering College, Shijiazhuang 050003, China e-mail: [email protected]
*
*Corresponding author.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let C be a non-empty closed convex subset of a reflexive and strictly convex Banach space E which also has a weakly continuous duality map Jφ(x) with the gauge φ. Let S and T be non-expansive mappings from C into itself such that F = F(S) ∩ F(T) ≠ ∅. Let {αn} and {βn} be sequences in (0, 1). Let {xn} be a sequence defined by 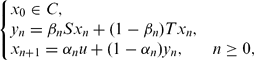where u ∈ C is a given point. Assume that the following restrictions imposed on the control sequences are satisfied:

Then the sequence {xn} converges strongly to x* ∈ F, where x* = Q(u) and Q: C → F is the unique sunny non-expansive retraction from C onto F.

Keywords

47H0947H1047J25
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 52 , Issue 2 , May 2010 , pp. 241 - 252
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Browder, F. E., Fixed point theorems for noncompact mappings in Hilbert spaces, Proc. Natl. Acad. Sci. USA 53 (1965), 1272–1276.Google Scholar
2.Browder, F. E., Convergence theorems for sequences of nonlinear operators in Banach spaces, Math. Z. 100 (1967), 201–225.Google Scholar
3.Bruck, R. E., Properties of fixed point sets of nonexpansive mappings in Banach spaces, Trans. Amer. Math. Soc. 179 (1973), 251–262.CrossRefGoogle Scholar
4.Censor, Y. and Zenios, S. A., Parallel Optimization. Theory, Algorithms, and Applications, Numerical Mathematics and Scientific Computation (Oxford University Press, New York, 1997).Google Scholar
5.Cho, Y. J., Kang, S. M. and Qin, X., Approximation of common fixed points of an infinite family of nonexpansive mappings in Banach spaces, Comput. Math. Appl. 56 (2008), 2058–2064.Google Scholar
6.Cho, Y. J., Kang, S. M. and Qin, X., Convergence theorems of fixed points for a finite family of nonexpansive mappings in Banach spaces, Fixed Point Theory Appl. 2008 (2008), 1–6.Google Scholar
7.Cho, Y. J. and Qin, X., Convergence of a general iterative method for nonexpansive mappings in Hilbert spaces, J. Comput. Appl. Math. 228 (2009), 458–465.CrossRefGoogle Scholar
8.Combettes, P. L., The convex feasibility problem: In image recovery, Advances in Imaging and Electron Physics (Hawkes, P., Editor) (Academic Press, Orlando, FA, 1996), vol. 95, pp. 155–270.Google Scholar
9.Goebel, K. and Reich, S., Uniform convexity, hyperbolic geometry and nonexpansive mappings (Dekker, New York, 1984).Google Scholar
10.Halpern, B., Fixed points of nonexpanding maps, Bull. Amer. Math. Soc. 73 (1967), 957–961.CrossRefGoogle Scholar
11.Kim, T. H. and Xu, H. K., Strong convergence of modified Mann iterations, Nonlinear Anal. 61 (2005), 51–60.CrossRefGoogle Scholar
12.Kimura, Y., Takahashi, W. and Toyoda, M., Convergence to common fixed points of a finite family of nonexpansive mappigns, Arch. Math. 84 (2005), 350–363.CrossRefGoogle Scholar
13.Kotzer, T., Cohen, N. and Shamir, J., Images to ration by a novel method of parallel projection onto constraint sets, Opt. Lett. 20 (1995), 1172–1174.Google Scholar
14.Lim, T. C. and Xu, H. K., Fixed point theorems for asymptotically nonexpansive mappings, Nonlinear Anal. 22 (1994), 1345–1355.Google Scholar
15.Lions, P. L., Approximation de points fixes de contractions, C.R. Acad. Sci. Sèr. A-B Paris 284 (1977), 1357–1359.Google Scholar
16.Mann, W. R., Mean value methods in iteration, Proc. Amer. Math. Soc. 4 (1953), 506–510.Google Scholar
17.Nakajo, K. and Takahashi, W., Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups, J. Math. Anal. Appl. 279 (2003), 372–379.CrossRefGoogle Scholar
18.Qin, X., Cho, Y. J., Kang, J. I. and Kang, S. M., Strong convergence theorems for an infinite family of nonexpansive mappings in Banach spaces, J. Comput. Appl. Math. 230 (2009), 121–127.Google Scholar
19.Qin, X. and Su, Y., Approximation of a zero point of accretive operator in Banach spaces, J. Math. Anal. Appl. 329 (2007), 415–424.Google Scholar
20.Qin, X., Su, Y. and Shang, M., Strong convergence of the composite Halpern iteration, J. Math. Anal. Appl. 339 (2008), 996–1002.CrossRefGoogle Scholar
21.Qin, X., Su, Y. and Wu, C., Strong convergence theorems for nonexpansive mappings by viscosity approximation methods in Banach spaces, Math. J. Okayama Univ. 50 (2008), 113–125.Google Scholar
22.Reich, S., Weak convergence theorems for nonexpansive mappings in Banach spaces, J. Math. Anal. Appl. 67 (1979), 274–276.CrossRefGoogle Scholar
23.Reich, S., Strong convergence theorems for resolvents of accretive operators in Banach spaces, J. Math. Anal. Appl. 75 (1980), 287–292.Google Scholar
24.Su, Y. and Qin, X., Strong convergence theorems for asymptotically nonexpansive mappings and asymptotically nonexpansive semigroups, Fixed Point Theory Appl. 2006 (2006), 1–11.Google Scholar
25.Sezan, M. I. and Stark, H., Application of convex projection theory to image recovery in tomograph and related areas, in Image Recovery: Theory and Application (Stark, H., Editor) (Academic Press, Orlando, FA, 1987) pp. 155–270.Google Scholar
26.Suzuki, T., Strong convergence theorem to common fixed points of two nonexpansive mappings in general Banach spaces, J. Nonlinear Convex Anal. 3 (2002), 381–391.Google Scholar
27.Suzuki, T., Moudafi's viscosity approximations with Meir–Keeler contractions, J. Math. Anal. Appl. 325 (2007), 342–352.Google Scholar
28.Wittmann, R., Approximation of fixed points of nonexpansive mappings, Arch. Math. 58 (1992), 486–491.Google Scholar
29.Xu, H. K., Another control condition in an iterative method for nonexpansive mappings, Bull. Austral. Math. Soc. 65 (2002), 109–113.Google Scholar
30.Xu, H. K., Iterative algorithms for nonlinear operators, J. Lond. Math. Soc. 66 (2002), 240–256.Google Scholar
31.Xu, H. K., An iterative approach to quadratic optimization, J. Optim. Theory Appl. 116 (2003), 659–678.Google Scholar
32.Xu, H. K., Strong convergence of an iterative method for nonexpansive and accretive opertors, J. Math. Anal. Appl. 314 (2006), 631–643.Google Scholar
33.Yao, Y., Chen, R. and Yao, J. C., Strong convergence and certain control conditions for modified Mann iteration, Nonliner Anal. 68 (2008), 1687–1693.Google Scholar
34.Zhou, H., Convergence theorems for λ-strict pseudo-contractions in 2-uniformly smooth Banach spaces, Nonlinear Anal. 69 (2008), 3160–3173.Google Scholar