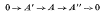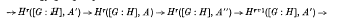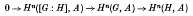Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hochschild, G.
1956.
Relative homological algebra.
Transactions of the American Mathematical Society,
Vol. 82,
Issue. 1,
p.
246.
Nakayama, Tadasi
1958.
Note on fundamental exact sequences in homology and cohomology for non-normal subgroups.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 34,
Issue. 10,
Nakayama, Tadasi
1959.
Higher dimensional cohomology groups in generalized quaternion algebras.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 23,
Issue. 1,
p.
174.
Rosenberg, Alex
and
Zelinsky, Daniel
1960.
On Amitsur’s complex.
Transactions of the American Mathematical Society,
Vol. 97,
Issue. 2,
p.
327.
Nakayama, Tadasi
1960.
A Remark on Relative Homology and Cohomology Groups of a Group.
Nagoya Mathematical Journal,
Vol. 16,
Issue. ,
p.
1.
Nakayama, Tadasi
1961.
Fundamental Exact Sequences in (co)-Homology for Non-Normal Subgroups.
Nagoya Mathematical Journal,
Vol. 18,
Issue. ,
p.
63.
Pareigis, Bodo
1964.
�ber normale, zentrale, separable Algebren und Amitsur-Kohomologie.
Mathematische Annalen,
Vol. 154,
Issue. 4,
p.
330.
1969.
Vol. 34,
Issue. ,
p.
267.
Katayama, Shin-ichi
1986.
Class number relations of algebraic Tori, II.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 62,
Issue. 8,
JoséMartinez, Jusn
1990.
A relative description of a cohomolgy of representations.
Communications in Algebra,
Vol. 18,
Issue. 2,
p.
473.
Muzere, Mark
1990.
Relative Lie algebra cohomology revisited.
Proceedings of the American Mathematical Society,
Vol. 108,
Issue. 3,
p.
665.
1993.
Continuation of the Notas de Matemàtica.
Vol. 177,
Issue. ,
p.
831.
Arciniega-Nevárez, José Antonio
and
Cisneros-Molina, José Luis
2017.
Comparison of relative group (co)homologies.
Boletín de la Sociedad Matemática Mexicana,
Vol. 23,
Issue. 1,
p.
41.
Galindo, César
and
Morales, Yiby
2019.
A five-term exact sequence for Kac cohomology.
Algebra & Number Theory,
Vol. 13,
Issue. 5,
p.
1121.
Dyckerhoff, Tobias
and
Kapranov, Mikhail
2019.
Higher Segal Spaces.
Vol. 2244,
Issue. ,
p.
9.
Ariciniega-Nevárez, José Antonio
Cisneros-Molina, José Luis
and
Sánchez Saldaña, Luis Jorge
2021.
Relative group homology theories with coefficients and the comparison homomorphism.
Quaestiones Mathematicae,
Vol. 44,
Issue. 8,
p.
1107.
Błaszczyk, Zbigniew
Carrasquel-Vera, José Gabriel
and
Espinosa Baro, Arturo
2022.
On the sectional category of subgroup inclusions and Adamson cohomology theory.
Journal of Pure and Applied Algebra,
Vol. 226,
Issue. 6,
p.
106959.
Inassaridze, Hvedri
2022.
(Co)homology of $$\Gamma $$-groups and $$\Gamma $$-homological algebra.
European Journal of Mathematics,
Vol. 8,
Issue. S2,
p.
720.
Inassaridze, Hvedri
2023.
Equivariant algebraic K-functors for $$\Gamma $$-rings.
European Journal of Mathematics,
Vol. 9,
Issue. 4,
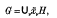
 v. In this paper we construct a “coset space complex” and assign cohomology groups; Hr([G: H], A), to it for all coefficient modules A and all dimensions, -∞<r<∞. We show that if
v. In this paper we construct a “coset space complex” and assign cohomology groups; Hr([G: H], A), to it for all coefficient modules A and all dimensions, -∞<r<∞. We show that if