Hostname: page-component-f554764f5-8cg97 Total loading time: 0 Render date: 2025-04-12T00:11:36.678Z Has data issue: false hasContentIssue false
  • English
  • Français

Codazzi and totally umbilical hypersurfaces in 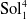$\mathrm {Sol}_1^4$

Part of: Global differential geometry

Published online by Cambridge University Press:  03 April 2025

Zlatko Erjavec Open the ORCID record for Zlatko Erjavec [Opens in a new window]  and
Jun-ichi Inoguchi Open the ORCID record for Jun-ichi Inoguchi [Opens in a new window]
Zlatko Erjavec*
Affiliation:
Faculty of Organization and Informatics, University of Zagreb, Varaždin, Croatia
Jun-ichi Inoguchi
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo, Japan
*
Corresponding author: Zlatko Erjavec; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove the non-existence of Codazzi and totally umbilical hypersurfaces, especially totally geodesic hypersurfaces, in the 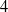$4$-dimensional model space 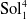$\mathrm {Sol}_1^4$.

Keywords

Codazzi hypersurfaceparallel hypersurfacetotally umbilicaltotally geodesicsolvable Lie group

MSC classification

Primary: 53C30: Homogeneous manifolds
Secondary: 53C42: Immersions (minimal, prescribed curvature, tight, etc.) 53C40: Global submanifolds
Type
Research Article
Information
Glasgow Mathematical Journal , First View , pp. 1 - 7
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

†

The authors dedicate this article to Professor Toshiyuki Akita on the occasion of his 60th birthday.

References

Ayad, Y. and Fahlaoui, S., Isometry groups of simply connected unimodular $4$ -dimensional Lie groups, 2024. https://arxiv.org/pdf/2412.01588Google Scholar
Chen, B.-Y., Classification of locally symmetric spaces which admit a totally umbilical hypersurface, Soochow J. Math. 6 (1980), 39–48.Google Scholar
Chen, B.-Y., Classification of totally umbilical submanifolds in symmetric spaces, J. Aust. Math. Soc., Ser. A 30 (1980), 129–136.Google Scholar
Chen, B.-Y., Extrinsic spheres in Kähler manifolds, Michigan Math. J. 23(4) (1976), 327–330.Google Scholar
Chen, B.-Y., Extrinsic spheres in Kähler manifolds. II., Michigan Math. J. 24(1) (1977), 97–102.Google Scholar
Chen, B.-Y., Totally umbilical submanifolds of Hermitian symmetric spaces, Soochow J. Math. 4 (1978), 17–28.Google Scholar
Chen, B.-Y., Totally umbilical submanifolds of Kaehler manifolds, Arch. Math. 36 (1981), 83–91.Google Scholar
Chen, B.-Y. and Nagano, T., Totally geodesic submanifolds of symmetric spaces. II., Duke Math. J. 45 (1978), 405–425.CrossRefGoogle Scholar
Chen, B.-Y. and Ogiue, K., Two theorems on Kähler manifolds, Michigan Math. J. 21 (1974), 225–229.Google Scholar
Chen, B.-Y. and Verheyen, P., Totally umbilical submanifolds of Kaehler manifolds. II., Bull. Soc. Math. Belg., Sér. B 35 (1983), 27–44.Google Scholar
De Leo, B. and Van der Veken, J., Totally geodesic hypersurfaces of four-dimensional generalized symmetric spaces, Geom. Dedicata 159 (2012), 373–387.Google Scholar
D’haene, M., Thurston geometries in dimension four from a Riemannian perspective, 2024. https://arxiv.org/pdf/2401.05977 Google Scholar
D’haene, M., Inoguchi, J. and Van der Veken, J., Parallel and totally umbilical hypersurfaces of the four dimensional Thurston geometry $\mathrm {Sol}^4_0$ , Math. Nachr. 297(5) (2024), 1879–1891.CrossRefGoogle Scholar
Djellali, N., Hasni, A., Cherif, A. M. and Belkhelfa, M., Classification of Codazzi and note on minimal hypersurfaces in $Nil^4$ , Int. Electron. J. Geom. 16(2) (2023), 707–714.CrossRefGoogle Scholar
Erjavec, Z. and Inoguchi, J., Minimal submanifolds in $\mathrm {Sol}^4_0$ , J. Geom. Anal. 33(9) (2023), 39.Paper No. 274CrossRefGoogle Scholar
Erjavec, Z. and Inoguchi, J., Minimal submanifolds in $\mathrm {Sol}^4_1$ , Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat., RACSAM 117(4) (2023), 36.Paper no. 156Google Scholar
Erjavec, Z. and Inoguchi, J., Geodesics and magnetic curves in the 4-dim almost Kähler model space $\mathrm {F}^4$ , Complex Manifolds 11 (2024), 33.Article ID 20240001CrossRefGoogle Scholar
Filipkiewicz, R., Four dimensional geometries, PhD Thesis (University of Warwick, 1983). http://webcat.warwick.ac.uk/record=b1462578~S9 Google Scholar
Inoguchi, J., Homogeneous geodesics of $4$ -dimensional solvable Lie groups, Int. Electron. J. Geom. 17(1) (2024), 106–136.CrossRefGoogle Scholar
Inoue, M., On surfaces of class $\mathrm {VII}_0$ , Invent. Math. 24 (1974), 269–310.CrossRefGoogle Scholar
Klein, S., Totally geodesic submanifolds of the complex quadric, Differ. Geom. Appl. 26(1) (2008), 79–96.CrossRefGoogle Scholar
Lee, K. B. and Thuong, S., Infra-solvmanifolds of $\mathrm {Sol}^4_1$ , J. Korean Math. Soc. 52(6) (2015), 1209–1251.CrossRefGoogle Scholar
Munteanu, M. I., Minimal submanifolds in $\mathbb {R}^4$ with a globally conformal Kähler structure, Czech Math. J. 58 (2008), 61–78.CrossRefGoogle Scholar
Nikolayevsky, Y., Totally geodesic hypersurfaces of homogeneous spaces, Israel J. Math. 207(1) (2015), 361–375.CrossRefGoogle Scholar
Sawai, H., A non-Vaisman LCK solvmanifold associated to a one-dimensional extension of a 2-step nilmanifold, Differ. Geom. Appl. 96 (2024), 11. Article ID 102174CrossRefGoogle Scholar
Tricerri, F., Some examples of locally conformal Kähler manifolds, Rend. Sem. Mat. Torino 40(1) (1982), 81–92.Google Scholar
Tsukada, K., Totally geodesic hypersurfaces of naturally reductive homogeneous spaces, Osaka J. Math. 33(3) (1996), 697–707.Google Scholar
Tsukada, K., Totally geodesic submanifolds of Riemannian manifolds and curvature-invariant subspaces, Kodai Math. J. 19(3) (1996), 395–437.Google Scholar
Van Thuong, S., Classification, cobordism, and curvature of four-dimensional infra-solvmanifolds, PhD Thesis (University of Oklahoma, 2014). http://hdl.handle.net/11244/10360 Google Scholar
Van Thuong, S., Metrics on $4$ -dimensional unimodular Lie groups, Ann. Global Anal. Geom. 51(2) (2017), 109–128.CrossRefGoogle Scholar
Wall, C. T. C., Geometries and geometric structures in real dimension 4 and complex dimension 2, in Geometry and Topology. Lecture Notes in Math. vol. 1167, (1985), 268–292.Google Scholar