Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-13T00:54:28.258Z Has data issue: false hasContentIssue false
  • English
  • Français

CHARACTERS OF PRIME DEGREE

Published online by Cambridge University Press:  01 August 2011

EDITH ADAN-BANTE
EDITH ADAN-BANTE*
Affiliation:
Department of Mathematical Science, Northern Illinois University, Watson Hall 320, DeKalb, IL 60115-2888, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a finite nilpotent group, χ and ψ be irreducible complex characters of G with prime degree. Assume that χ(1) = p. Then, either the product χψ is a multiple of an irreducible character or χψ is the linear combination of at least 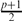distinct irreducible characters.

Keywords

20c15
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 53 , Issue 3 , September 2011 , pp. 419 - 426
Copyright
Copyright © Glasgow Mathematical Journal Trust 2011

References

REFERENCES

1.Adan-Bante, E., Products of characters and finite p-groups, J. Algebra 277 (2004) 236–255.CrossRefGoogle Scholar
2.Adan-Bante, E., Products of characters and finite p-groups II, Arch. Math. 82 (4) (2004), 289–297.CrossRefGoogle Scholar
3.Adan-Bante, E., Products of characters and derived length II, J. Group Theory 8 (2005), 453–459.CrossRefGoogle Scholar
4.Adan-Bante, E., Restriction of characters and products of characters, Israel J. Math 174 (1) (2009), 221–225.CrossRefGoogle Scholar
5.Isaacs, I. M., Character theory of finite groups (Academic Press, New York-San Francisco–London, 1976)Google Scholar
6.Loukaki, M. and Moreto, A., On the number of constituents of products of characters, Algebra Colloq. 14 (2) (2007), 207–208.CrossRefGoogle Scholar