Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-24T00:46:32.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterization of certain differential operators in the solution of linear partial differential equations†

Published online by Cambridge University Press:  18 May 2009

Rudolf Heersink
Rudolf Heersink
Affiliation:
University of GlasgowDepartment of MathematicsUniversity GardensGlasgow G12 8QW
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider differential equations of the form

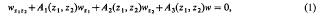
where the coefficients Ai are holomorphic functions in a domain G1 × G2 ⊂ C × C. We restrict our attention to those equations for which it is possible to represent the solutions in the form

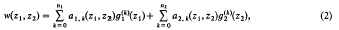
where g1(z1) and g2(z2) are arbitrary holomorphic functions in G1 and G2 respectively. The coefficients a1, k and a2, k depend on the given differential equation. Within the last ten years a number of publications have been devoted to this kind of representation of solutions.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 17 , Issue 2 , July 1976 , pp. 83 - 88
Copyright
Copyright © Glasgow Mathematical Journal Trust 1976

References

REFERENCES

1.Bauer, K. W. and Florian, H., Bergman-Operatoren mit Polynomerzeugenden, Applicable Anal.; to appear.Google Scholar
2.Bieberbach, L., Theorie der gewöhnlichen Differentialgleichungen. Auf funktionentheoretischer Grundlage dargestellt (Springer, 1953).Google Scholar
3.Vekua, I. N., New methods for solving elliptic equations (North Holland Publishing Company, 1968).Google Scholar
4.Watzlawek, W., Über lineare partielle Differentialgleichungen zweiter Ordnung mit Fundamentalsystemen, J. Reine Angew. Math. 247 (1971), 69–74.Google Scholar
5.Watzlawek, W., Über Zusammenhänge zwischen Fundamentalsystemen, Riemannfunktion und Bergman-Operatoren, J. Reine Angew, Math. 251 (1971), 200–211.Google Scholar