Article contents
Bounded completeness and Schauder's basis for C[0, 1]
Published online by Cambridge University Press: 18 May 2009
Extract
A basis 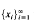 , for a Banach space X is said to be boundedly complete [4, p. 284] if whenever
, for a Banach space X is said to be boundedly complete [4, p. 284] if whenever 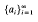 is a sequence of scalars for which
is a sequence of scalars for which 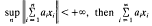 converges. It is well-known [2, p. 70] that if
converges. It is well-known [2, p. 70] that if 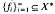 is a boundedly complete basis for X then X is isometric to a conjugate space; in fact, X = [fi]*, where
is a boundedly complete basis for X then X is isometric to a conjugate space; in fact, X = [fi]*, where 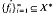 is the sequence of coefficient functionals associated with the basis
is the sequence of coefficient functionals associated with the basis 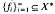 It follows that no basis for C[0,1] can be boundedly complete since no separable conjugate space contains C0[l], yet C[0,1] is a separable space which contains c0.
It follows that no basis for C[0,1] can be boundedly complete since no separable conjugate space contains C0[l], yet C[0,1] is a separable space which contains c0.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1986
References
REFERENCES
- 3
- Cited by


