Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T10:46:00.591Z Has data issue: false hasContentIssue false
  • English
  • Français

THE BOUNDED APPROXIMATION PROPERTY FOR THE WEIGHTED SPACES OF HOLOMORPHIC MAPPINGS ON BANACH SPACES

Part of: Measures, integration, derivative, holomorphy Normed linear spaces and Banach spaces; Banach lattices Linear function spaces and their duals

Published online by Cambridge University Press:  07 September 2017

MANJUL GUPTA  and
DEEPIKA BAWEJA
MANJUL GUPTA
Affiliation:
Department of Mathematics and Statistics, IIT Kanpur, Kanpur208016, India e-mails: [email protected], [email protected]
DEEPIKA BAWEJA
Affiliation:
Department of Mathematics and Statistics, IIT Kanpur, Kanpur208016, India e-mails: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study the bounded approximation property for the weighted space 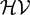$\mathcal{HV}$(U) of holomorphic mappings defined on a balanced open subset U of a Banach space E and its predual 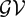$\mathcal{GV}$(U), where 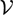$\mathcal{V}$ is a countable family of weights. After obtaining an 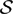$\mathcal{S}$-absolute decomposition for the space 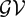$\mathcal{GV}$(U), we show that E has the bounded approximation property if and only if 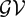$\mathcal{GV}$(U) has. In case 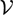$\mathcal{V}$ consists of a single weight v, an analogous characterization for the metric approximation property for a Banach space E has been obtained in terms of the metric approximation property for the space 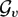$\mathcal{G}_v$(U).

MSC classification

Primary: 46B28: Spaces of operators; tensor products; approximation properties
Secondary: 46E50: Spaces of differentiable or holomorphic functions on infinite-dimensional spaces 46G20: Infinite-dimensional holomorphy
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 60 , Issue 2 , May 2018 , pp. 307 - 320
Copyright
Copyright © Glasgow Mathematical Journal Trust 2017 

References

REFERENCES

1. Beltran, M. J., Linearization of weighted (LB)-spaces of entire functions on Banach spaces, Rev. R. Acad. Cienc. Exactas Fīs. Nat., Ser. A Mat. 106 (1) (2012), 275–286.Google Scholar
2. Bierstedt, K. D., Bonet, J. and Galbis, A., Weighted spaces of holomorphc functions on Balanced domains, Michigan Math. J. 40 (2) (1993), 271–297.Google Scholar
3. Bierstedt, K. D. and Bonet, J., Biduality in Frechet and (LB)-spaces, in Progress in functional anlysis (Bierstedt, K. D. et al., Editors), North Holland Math. Stud., vol. 170 (Elsevier Science Publishing Co., Amsterdam, 1992), 113–133.Google Scholar
4. Bierstedt, K. D., Miese, R. G. and Summers, W. H., A projective description of weighted inductive limits, Trans. Am. Math. Soc. 272 (1) (1982), 107–160.Google Scholar
5. Bierstedt, K. D., Gewichtete Raume stetiger vektorwertiger Funktionen und das injektive Tensorprodukt II, J. Reine Angew. Math. 260 (1973), 133–146.Google Scholar
6. Bierstedt, K. D. and Summers, W. H., Biduals of weighted Banach spaces of analytic functions, J. Austral. Math. Soc. Ser. A 54 (1) (1993), 70–79.Google Scholar
7. Boyd, C., Dineen, S. and Rueda, P., Weakly uniformly continuous holomorphic functions and the approximation property, Indag. Math.(N.S.) 12 (2) (2001), 147–156.Google Scholar
8. Caliskan, E., Approximation of holomorphic mappings on infinite dimensional spaces, Rev. Mat. Complut. 17 (2) (2004), 411–434.Google Scholar
9. Caliskan, E., The bounded approximation property for the predual of the space of bounded holomorphic mappings, Studia Math. 177 (3) (2006), 225–233.Google Scholar
10. Caliskan, E., The bounded approximation property for spaces of holomorphic mappings on infinite dimensional spaces, Math. Nachr. 279 (7) (2006), 705–715.Google Scholar
11. Caliskan, E., The bounded approximation property for weakly uniformly continuous type holomorphic mappings, Extracta Math. 22 (2) (2007), 157–177.Google Scholar
12. Dineen, S., Complex analysis in locally convex spaces, North-Holland Math. Studies, vol. 57 (North-Holland Publishing Co., Amsterdam, 1981).Google Scholar
13. Dineen, S., Complex analysis on infinite dimensional spaces (Springer-Verlag, London, 1999).CrossRefGoogle Scholar
14. Galindo, P., Garcia, D. and Maestre, M., Holomorphic mappings bounded type, J. Math. Anal. Appl. 166 (1) (1992), 236–246.CrossRefGoogle Scholar
15. Garcia, D., Maestre, M. and Rueda, P., Weighted spaces of holomorphic functions on Banach spaces, Studia Math. 138 (1) (2000), 1–24.Google Scholar
16. Garcia, D., Maestre, M. and Sevilla-peris, P., Weakly compact composition operators between weighted spaces, Note Mat. 25 (1) (2005/06), 205–220.Google Scholar
17. Grothendieck, A., Produits tensoriels topologiques et espaces nucléaires, Mem. Am. Math. Soc. (16), 1955.Google Scholar
18. Gupta, M. and Baweja, D., Weighted spaces of holomorphic functions on banach spaces and the approximation property, Extracta Math. 31 (2) (2016), 123–144.Google Scholar
19. Horvath, J., Topological vector spaces and distributions (Addison-Wesley, London, 1966).Google Scholar
20. Jorda, E., Weighted vector-valued holomorphic functions on Banach spaces abstract and applied analysis, vol. 2013 (Hindawi Publishing Corporation, Cairo, Egypt, 2013).Google Scholar
21. Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces. I, Ergeb. Math. Grenzgeb., Bd., vol. 92 (Springer, Berlin, 1977).Google Scholar
22. Mujica, J., Linearization of bounded holomorphic mappings on Banach spaces, Trans. Am. Math. Soc. 324 (2) (1991), 867–887.Google Scholar
23. Mujica, J., Complex analysis in Banach spaces, North-Holland Math. Studies, vol. 120, (North-Holland Publishing Co., Amsterdam, 1986).Google Scholar
24. Mujica, J., Linearization of holomorphic mappings of bounded type, in Progress in functional analysis (Biersted, K. D. et al., Editors) North Holland Math. Stud., vol. 170 (Elsevier Science Publishing Co., Amsterdam, 1992), 149–162.Google Scholar
25. Mujica, J. and Nachbin, L., Linearization of holomorphic mappings on locally convex spaces, J. Math. Pures. Appl. 71 (6) (1992), 543–560.Google Scholar
26. Nachbin, L., Topology on spaces of holomorphic mappings (Springer-Verlag, New York, 1969).Google Scholar
27. Ng, K. F., On a theorem of Dixmier, Math. Scand. 29 (1971), 279–280.Google Scholar
28. Rubel, L. A. and Shields, A. L., The second duals of certain spaces of analytic functions, J. Austral. Math. Soc. 11 (3) (1970), 276–280.Google Scholar
29. Rueda, P., On the banach dieudonne theorem for spaces of holomorphic functions, Quaestiones Math. 19 (1-2) (1996), 341–352.Google Scholar
30. Ryan, R., Applications of topological tensor products to infinite dimensional holomorphy, PhD Thesis (Trinity College, Dublin, 1980).Google Scholar