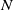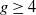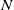1. Introduction
Let
![]() $N=N_{{g},p}^{b}$
be a connected nonorientable surface of genus
$N=N_{{g},p}^{b}$
be a connected nonorientable surface of genus
![]() ${g}\geq 1$
with
${g}\geq 1$
with
![]() $b\geq 0$
boundary components and
$b\geq 0$
boundary components and
![]() $p\geq 0$
punctures, and
$p\geq 0$
punctures, and
![]() $S=S_{h,p}^{b}$
a connected orientable surface of genus
$S=S_{h,p}^{b}$
a connected orientable surface of genus
![]() $h\geq 0$
with
$h\geq 0$
with
![]() $b\geq 0$
boundary components and
$b\geq 0$
boundary components and
![]() $p\geq 0$
punctures. Note that
$p\geq 0$
punctures. Note that
![]() $N_{{g},p}^{b}$
is homeomorphic to the surface obtained from a sphere with
$N_{{g},p}^{b}$
is homeomorphic to the surface obtained from a sphere with
![]() $p$
punctures by removing
$p$
punctures by removing
![]() ${g}+b$
open disks and attaching
${g}+b$
open disks and attaching
![]() $g$
Möbius bands along their boundaries, and we call each of the Möbius bands a crosscap. We drop the subscript
$g$
Möbius bands along their boundaries, and we call each of the Möbius bands a crosscap. We drop the subscript
![]() $b$
(resp.
$b$
(resp.
![]() $p$
) from
$p$
) from
![]() $N_{{g},p}^{b}$
and
$N_{{g},p}^{b}$
and
![]() $S_{h,p}^{b}$
if
$S_{h,p}^{b}$
if
![]() $b=0$
(resp.
$b=0$
(resp.
![]() $p=0$
). In particular,
$p=0$
). In particular,
![]() $N_{{g}}=N_{{g},0}^0$
and
$N_{{g}}=N_{{g},0}^0$
and
![]() $S_{h}=S_{h,0}^0$
denote closed surfaces. If we do not care whether the surface is orientable or not, we write
$S_{h}=S_{h,0}^0$
denote closed surfaces. If we do not care whether the surface is orientable or not, we write
![]() $F=F_{k,p}^b$
for the surface.
$F=F_{k,p}^b$
for the surface.
In [Reference Bowden, Hensel and Webb2], Bowden, Hensel, and Webb introduced the fine curve graph
![]() $\mathcal{C}^{\dagger }(F)$
of a surface
$\mathcal{C}^{\dagger }(F)$
of a surface
![]() $F$
in order to study the homeomorphism group
$F$
in order to study the homeomorphism group
![]() $\mathrm{Homeo}(F)$
and the diffeomorphism group
$\mathrm{Homeo}(F)$
and the diffeomorphism group
![]() $\mathrm{Diff}(F)$
of
$\mathrm{Diff}(F)$
of
![]() $F$
. Here, the fine curve graph
$F$
. Here, the fine curve graph
![]() $\mathcal{C}^{\dagger }(F)$
of a surface
$\mathcal{C}^{\dagger }(F)$
of a surface
![]() $F$
is the graph whose vertices are essential simple closed curves in
$F$
is the graph whose vertices are essential simple closed curves in
![]() $F$
and whose edges correspond to pairs of vertices that are disjoint in
$F$
and whose edges correspond to pairs of vertices that are disjoint in
![]() $F$
. The action of
$F$
. The action of
![]() $\mathrm{Homeo}(F)$
on
$\mathrm{Homeo}(F)$
on
![]() $\mathcal{C}^{\dagger }(F)$
induces the natural map
$\mathcal{C}^{\dagger }(F)$
induces the natural map
![]() $\eta \colon \mathrm{Homeo}(F)\rightarrow \mathrm{Aut}(\mathcal{C}^{\dagger }(F))$
.
$\eta \colon \mathrm{Homeo}(F)\rightarrow \mathrm{Aut}(\mathcal{C}^{\dagger }(F))$
.
In [Reference Long, Margalit, Pham, Verberne and Yao5], Long, Margalit, Pham, Verberne, and Yao proved that the natural map
![]() $\eta \colon \mathrm{Homeo}(S_{h})\rightarrow \mathrm{Aut}(\mathcal{C}^{\dagger }(S_{h}))$
is an isomorphism for
$\eta \colon \mathrm{Homeo}(S_{h})\rightarrow \mathrm{Aut}(\mathcal{C}^{\dagger }(S_{h}))$
is an isomorphism for
![]() $h\geq 2$
. In this paper, we extend their result to nonorientable surfaces. Namely, we prove the following:
$h\geq 2$
. In this paper, we extend their result to nonorientable surfaces. Namely, we prove the following:
Theorem 1.1. For
![]() ${g}\geq 4$
, the natural map
${g}\geq 4$
, the natural map
![]() $\eta \colon \mathrm{Homeo}(N_{{g}})\rightarrow \mathrm{Aut}(\mathcal{C}^{\dagger }(N_{{g}}))$
is an isomorphism.
$\eta \colon \mathrm{Homeo}(N_{{g}})\rightarrow \mathrm{Aut}(\mathcal{C}^{\dagger }(N_{{g}}))$
is an isomorphism.
The result of [Reference Long, Margalit, Pham, Verberne and Yao5] can be thought of as an analogy to the classical result of Ivanov [Reference Ivanov3], which states that the automorphism group
![]() $\textrm{Aut}(\mathcal{C}(S_{h}))$
of the ordinary curve graph
$\textrm{Aut}(\mathcal{C}(S_{h}))$
of the ordinary curve graph
![]() $\mathcal{C}(S_{h})$
is isomorphic to the extended mapping class group
$\mathcal{C}(S_{h})$
is isomorphic to the extended mapping class group
![]() $\mathrm{Mod}^{\pm }(S_{h})$
of
$\mathrm{Mod}^{\pm }(S_{h})$
of
![]() $S_{h}$
if
$S_{h}$
if
![]() $h \geq 3$
. Similarly, Theorem 1.1 can also be thought of as an analogy to the result of Atalan and Korkmaz [Reference Atalan and Korkmaz1], which states that the automorphism group
$h \geq 3$
. Similarly, Theorem 1.1 can also be thought of as an analogy to the result of Atalan and Korkmaz [Reference Atalan and Korkmaz1], which states that the automorphism group
![]() $\textrm{Aut}(\mathcal{C}(N_{{g}}))$
of the ordinary curve graph
$\textrm{Aut}(\mathcal{C}(N_{{g}}))$
of the ordinary curve graph
![]() $\mathcal{C}(N_{g})$
is isomorphic to the mapping class group
$\mathcal{C}(N_{g})$
is isomorphic to the mapping class group
![]() $\mathrm{Mod}(N_{{g}})$
of
$\mathrm{Mod}(N_{{g}})$
of
![]() $N_{g}$
if
$N_{g}$
if
![]() ${{g}} \geq 5$
.
${{g}} \geq 5$
.
To prove Theorem 1.1, we apply the argument in [Reference Long, Margalit, Pham, Verberne and Yao5], but with some modifications. For nonorientable surfaces, we need to consider the following differences from orientable surfaces:
-
• Not only two-sided curves but also one-sided curves appear on a nonorientable surface. Thus, it is necessary to properly define whether one-sided curves are allowed or not for several concepts, such as torus pairs, pants pairs, and bigon pairs (see Subsection 2.1). We also observe that automorphisms of
 $\mathcal{C}^{\dagger }(N)$
preserve two-sidedness of curves (Lemma 3.6).
$\mathcal{C}^{\dagger }(N)$
preserve two-sidedness of curves (Lemma 3.6). -
• Inessential simple closed curves of closed nonorientable surfaces consist not only of curves bounding a disk but also of curves bounding a Möbius band. This affects the proofs of Lemmas 3.7 and 3.9 for example. We also have to consider whether or not curves bounding a Möbius band are allowed in our definition of the extended fine curve graph
 $\mathcal{EC}^{\dagger }(N)$
(see Remark 6.2).
$\mathcal{EC}^{\dagger }(N)$
(see Remark 6.2).
In related research, Le Roux and Wolff [Reference Roux and Wolff6] considered a variant
![]() $\mathcal{NC}_{\pitchfork }^{\dagger }(F)$
of the fine curve graph and its automorphism group. They proved that
$\mathcal{NC}_{\pitchfork }^{\dagger }(F)$
of the fine curve graph and its automorphism group. They proved that
![]() $\textrm{Aut}(\mathcal{NC}_{\pitchfork }^{\dagger }(F))$
is isomorphic to
$\textrm{Aut}(\mathcal{NC}_{\pitchfork }^{\dagger }(F))$
is isomorphic to
![]() $\textrm{Homeo}(F)$
for every nonspherical surface (i.e., surfaces not embeddable in the 2-sphere) without boundary, orientable or not, compact or not. In [Reference Roux and Wolff6], they mentioned the possibility of proving the result of [Reference Long, Margalit, Pham, Verberne and Yao5] via the graph
$\textrm{Homeo}(F)$
for every nonspherical surface (i.e., surfaces not embeddable in the 2-sphere) without boundary, orientable or not, compact or not. In [Reference Roux and Wolff6], they mentioned the possibility of proving the result of [Reference Long, Margalit, Pham, Verberne and Yao5] via the graph
![]() $\mathcal{NC}_{\pitchfork }^{\dagger }(F)$
. We hope that Theorem 1.1 could also be approached with the same strategy.
$\mathcal{NC}_{\pitchfork }^{\dagger }(F)$
. We hope that Theorem 1.1 could also be approached with the same strategy.
2. Preliminaries
2.1. Nonorientable surfaces
Throughout this paper, a curve in
![]() $F$
means a simple closed curve in
$F$
means a simple closed curve in
![]() $F$
, unless otherwise noted. A curve
$F$
, unless otherwise noted. A curve
![]() $c$
in a surface
$c$
in a surface
![]() $F$
is said to be one-sided if a regular neighborhood of
$F$
is said to be one-sided if a regular neighborhood of
![]() $c$
is a Möbius band, and
$c$
is a Möbius band, and
![]() $c$
is said to be two-sided if a regular neighborhood of
$c$
is said to be two-sided if a regular neighborhood of
![]() $c$
is an annulus. Every curve in an oriented surface is two-sided. We remark that a curve
$c$
is an annulus. Every curve in an oriented surface is two-sided. We remark that a curve
![]() $c$
in
$c$
in
![]() $N$
is one-sided (resp. two-sided) if and only if
$N$
is one-sided (resp. two-sided) if and only if
![]() $c$
passes through crosscaps an odd (resp. even) number of times.
$c$
passes through crosscaps an odd (resp. even) number of times.
For an orientable surface
![]() $S=S_{h}^b$
with
$S=S_{h}^b$
with
![]() $h\geq 1$
, the surface obtained by cutting
$h\geq 1$
, the surface obtained by cutting
![]() $S$
along a nonseparating curve is homeomorphic to
$S$
along a nonseparating curve is homeomorphic to
![]() $S_{h-1}^{b+2}$
. For a nonorientable surface
$S_{h-1}^{b+2}$
. For a nonorientable surface
![]() $N=N_{{g}}^b$
with
$N=N_{{g}}^b$
with
![]() ${g}\geq 1$
, let
${g}\geq 1$
, let
![]() $c$
be a nonseparating curve in
$c$
be a nonseparating curve in
![]() $N$
, and let
$N$
, and let
![]() $F$
denote the surface obtained by cutting
$F$
denote the surface obtained by cutting
![]() $N$
along
$N$
along
![]() $c$
. Then,
$c$
. Then,
-
•
 $F$
is homeomorphic to
$F$
is homeomorphic to
 $N_{{g}-1}^{b+1}$
or
$N_{{g}-1}^{b+1}$
or
 $S_{\frac{{g}-1}{2}}^{b+1}$
if
$S_{\frac{{g}-1}{2}}^{b+1}$
if
 $c$
is one-sided, and
$c$
is one-sided, and -
•
 $F$
is homeomorphic to
$F$
is homeomorphic to
 $N_{{g}-2}^{b+2}$
or
$N_{{g}-2}^{b+2}$
or
 $S_{\frac{{g}-2}{2}}^{b+2}$
if
$S_{\frac{{g}-2}{2}}^{b+2}$
if
 $c$
is two-sided.
$c$
is two-sided.
The following lemma, which will be used in the proof of Lemma 3.6, can be seen immediately from the above facts.
Lemma 2.1. Let
![]() $c$
be a nonseparating curve in a surface
$c$
be a nonseparating curve in a surface
![]() $F_{k}^b$
with
$F_{k}^b$
with
![]() $k \geq 1$
. Assume that the surface obtained by cutting
$k \geq 1$
. Assume that the surface obtained by cutting
![]() $F_{k}^b$
along
$F_{k}^b$
along
![]() $c$
is homeomorphic to
$c$
is homeomorphic to
![]() $F_{k'}^{b'}$
. Then
$F_{k'}^{b'}$
. Then
![]() $k \gt k'$
holds. Moreover, if
$k \gt k'$
holds. Moreover, if
![]() $F_{k}^b$
is nonorientable and
$F_{k}^b$
is nonorientable and
![]() $k-k'=1$
, then
$k-k'=1$
, then
![]() $c$
is one-sided.
$c$
is one-sided.
We can also observe the following fact. We will use it to prove Lemma 3.9 (1).
Lemma 2.2. Let
![]() $a$
and
$a$
and
![]() $b$
be disjoint nonseparating curves in a surface
$b$
be disjoint nonseparating curves in a surface
![]() $N_{g}$
with
$N_{g}$
with
![]() ${g} \geq 3$
. Assume that the surface obtained by cutting
${g} \geq 3$
. Assume that the surface obtained by cutting
![]() $N_g$
along
$N_g$
along
![]() $a$
and
$a$
and
![]() $b$
has two connected components
$b$
has two connected components
![]() $F$
and
$F$
and
![]() $F'$
. Then, there exists a separating essential curve in
$F'$
. Then, there exists a separating essential curve in
![]() $N_{g}$
that lies in
$N_{g}$
that lies in
![]() $F$
if and only if
$F$
if and only if
![]() $F$
is homeomorphic to neither
$F$
is homeomorphic to neither
![]() $S_0^2$
nor
$S_0^2$
nor
![]() $N_1^2$
.
$N_1^2$
.
2.2. Torus pairs, pants pairs, and bigon pairs
We define several concepts that appear in [Reference Long, Margalit, Pham, Verberne and Yao5] for nonorientable surfaces. We say that curves
![]() $c$
and
$c$
and
![]() $d$
in
$d$
in
![]() $N$
are noncrossing at a component
$N$
are noncrossing at a component
![]() $a$
of
$a$
of
![]() $c\cap d$
if there are a neighborhood
$c\cap d$
if there are a neighborhood
![]() $U$
of
$U$
of
![]() $a$
and a homeomorphism
$a$
and a homeomorphism
![]() $U\rightarrow \mathbb{R}^{2}$
such that the image of
$U\rightarrow \mathbb{R}^{2}$
such that the image of
![]() $c\cap U$
and
$c\cap U$
and
![]() $d\cap U$
lie in the (closed) upper and lower half plane of
$d\cap U$
lie in the (closed) upper and lower half plane of
![]() $\mathbb{R}^{2}$
, respectively (otherwise,
$\mathbb{R}^{2}$
, respectively (otherwise,
![]() $c$
and
$c$
and
![]() $d$
are called crossing at
$d$
are called crossing at
![]() $a$
). The curves
$a$
). The curves
![]() $c$
and
$c$
and
![]() $d$
are noncrossing if they are noncrossing at any component of
$d$
are noncrossing if they are noncrossing at any component of
![]() $c\cap d$
.
$c\cap d$
.
Let
![]() $c$
and
$c$
and
![]() $d$
be essential simple closed curves in
$d$
be essential simple closed curves in
![]() $N$
. We define torus pairs, pants pairs, and bigon pairs as follows:
$N$
. We define torus pairs, pants pairs, and bigon pairs as follows:
-
•
 $\{c,d\}$
is a torus pair if
$\{c,d\}$
is a torus pair if
 $c$
and
$c$
and
 $d$
are both two-sided,
$d$
are both two-sided,
 $c\cap d$
is a single interval, and
$c\cap d$
is a single interval, and
 $c$
and
$c$
and
 $d$
are crossing at that interval.
$d$
are crossing at that interval. -
•
 $\{c,d\}$
is a pants pair if
$\{c,d\}$
is a pants pair if
 $c$
and
$c$
and
 $d$
are both two-sided,
$d$
are both two-sided,
 $c\cap d$
is a single interval,
$c\cap d$
is a single interval,
 $c$
and
$c$
and
 $d$
are noncrossing at that interval, and
$d$
are noncrossing at that interval, and
 $c$
and
$c$
and
 $d$
are not homotopic.
$d$
are not homotopic. -
•
 $\{c,d\}$
is a bigon pair if
$\{c,d\}$
is a bigon pair if
 $c$
and
$c$
and
 $d$
are both two-sided,
$d$
are both two-sided,
 $c\cap d$
is just one nontrivial closed interval, and
$c\cap d$
is just one nontrivial closed interval, and
 $c$
and
$c$
and
 $d$
are homotopic.
$d$
are homotopic.
See Remark 3.8 for a discussion of why the definitions of torus pairs, pants pairs, and bigon pairs are restricted to two-sided curves.
A torus pair or a pants pair
![]() $\{c, d\}$
is degenerate if
$\{c, d\}$
is degenerate if
![]() $c\cap d$
is a single point. If
$c\cap d$
is a single point. If
![]() $\{c, d\}$
is a nondegenerate torus pair, then the curve
$\{c, d\}$
is a nondegenerate torus pair, then the curve
![]() $\overline{c\bigtriangleup d}\;:\!=\; \overline{c\cup d - c\cap d}$
is the remaining essential simple closed curve
$\overline{c\bigtriangleup d}\;:\!=\; \overline{c\cup d - c\cap d}$
is the remaining essential simple closed curve
![]() $e$
contained in
$e$
contained in
![]() $c\cup d$
, and we refer to
$c\cup d$
, and we refer to
![]() $\{c,d,e\}$
as a torus triple. We remark that if
$\{c,d,e\}$
as a torus triple. We remark that if
![]() $\{c, d\}$
is a nondegenerate torus pair, then the curve
$\{c, d\}$
is a nondegenerate torus pair, then the curve
![]() $\overline{c\bigtriangleup d}$
is two-sided. We can see this as follows. If the arc
$\overline{c\bigtriangleup d}$
is two-sided. We can see this as follows. If the arc
![]() $c\cap d$
passes the crosscaps an odd (resp. even) number of times, then both arcs
$c\cap d$
passes the crosscaps an odd (resp. even) number of times, then both arcs
![]() $c-c\cap d$
and
$c-c\cap d$
and
![]() $d-c\cap d$
also pass crosscaps an odd (resp. even) number of times since
$d-c\cap d$
also pass crosscaps an odd (resp. even) number of times since
![]() $c$
and
$c$
and
![]() $d$
are both two-sided curves. Then we see that the curve
$d$
are both two-sided curves. Then we see that the curve
![]() $\overline{c\bigtriangleup d} = \overline{(c-c\cap d) \cup (d-c\cap d)}$
is also two-sided since it passes the crosscaps an even number of times.
$\overline{c\bigtriangleup d} = \overline{(c-c\cap d) \cup (d-c\cap d)}$
is also two-sided since it passes the crosscaps an even number of times.
If
![]() $\{c, d\}$
is a bigon pair, then
$\{c, d\}$
is a bigon pair, then
![]() $e\;:\!=\;\overline{c\bigtriangleup d}$
is the simple closed curve, which bounds a disk. When the two curves in a bigon pair are nonseparating, we refer to the pair as a nonseparating bigon pair.
$e\;:\!=\;\overline{c\bigtriangleup d}$
is the simple closed curve, which bounds a disk. When the two curves in a bigon pair are nonseparating, we refer to the pair as a nonseparating bigon pair.
Moreover, we suppose that the bigon pairs
![]() $\{c,d\}$
and
$\{c,d\}$
and
![]() $\{c', d'\}$
determine the same inessential curve
$\{c', d'\}$
determine the same inessential curve
![]() $e$
bounding a disk. We say that the pair of bigon pairs
$e$
bounding a disk. We say that the pair of bigon pairs
![]() $\{\{c,d\}, \{c', d'\}\}$
is a sharing pair if the corresponding arcs connecting
$\{\{c,d\}, \{c', d'\}\}$
is a sharing pair if the corresponding arcs connecting
![]() $e$
have disjoint interiors. The sharing pair is linked if the corresponding arcs are linked at
$e$
have disjoint interiors. The sharing pair is linked if the corresponding arcs are linked at
![]() $e$
, which means that a curve parallel to
$e$
, which means that a curve parallel to
![]() $e$
and sufficiently close to
$e$
and sufficiently close to
![]() $e$
intersects the arcs alternately.
$e$
intersects the arcs alternately.
3. Key propositions
In this section, we provide an outline of the following key propositions for the proof of Theorem 1.1.
Proposition 3.1 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Proposition 2.1]). Let
![]() $N=N_{{g}}$
with
$N=N_{{g}}$
with
![]() ${g} \geq 4$
. Then every automorphism of
${g} \geq 4$
. Then every automorphism of
![]() $\mathcal{C}^{\dagger }(N)$
preserves the set of nonseparating bigon pairs.
$\mathcal{C}^{\dagger }(N)$
preserves the set of nonseparating bigon pairs.
Proposition 3.2 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Proposition 2.2]). Let
![]() $N=N_{{g}}$
with
$N=N_{{g}}$
with
![]() ${g} \geq 4$
. Then every automorphism of
${g} \geq 4$
. Then every automorphism of
![]() $\mathcal{C}^{\dagger }(N)$
preserves the set of linked sharing pairs.
$\mathcal{C}^{\dagger }(N)$
preserves the set of linked sharing pairs.
We also list the lemmas required for the key propositions. All propositions and lemmas in this section, except for Lemma 3.6, are taken from [Reference Long, Margalit, Pham, Verberne and Yao5, Section 2], with the surfaces modified to be nonorientable.
A multicurve is a finite collection of pairwise disjoint essential simple closed curves in
![]() $N$
. Note that a curve belonging to a multicurve may be one-sided or two-sided. A multicurve is separating if its complement has more than one component. We say that two curves
$N$
. Note that a curve belonging to a multicurve may be one-sided or two-sided. A multicurve is separating if its complement has more than one component. We say that two curves
![]() $a$
and
$a$
and
![]() $b$
lie in the same side of a separating multicurve
$b$
lie in the same side of a separating multicurve
![]() $m$
if they are disjoint from
$m$
if they are disjoint from
![]() $m$
and lie in the same complementary component. We remark that a separating multicurve
$m$
and lie in the same complementary component. We remark that a separating multicurve
![]() $m$
should contain at least one two-sided curve.
$m$
should contain at least one two-sided curve.
Lemma 3.3 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 2.3]). Let
![]() $N=N_{{g}}$
with
$N=N_{{g}}$
with
![]() ${g} \geq 3$
. Then every automorphism
${g} \geq 3$
. Then every automorphism
![]() $\alpha$
of
$\alpha$
of
![]() $\mathcal{C}^{\dagger }(N)$
preserves
$\mathcal{C}^{\dagger }(N)$
preserves
-
• the set of separating curves in
 $\mathcal{C}^{\dagger }(N)$
, and
$\mathcal{C}^{\dagger }(N)$
, and -
• the set of separating multicurves in
 $\mathcal{C}^{\dagger }(N)$
.
$\mathcal{C}^{\dagger }(N)$
.
Moreover,
![]() $\alpha$
preserves the sides of separating multicurves, that is,
$\alpha$
preserves the sides of separating multicurves, that is,
![]() $a$
and
$a$
and
![]() $b$
lie in the same side of a separating multicurve
$b$
lie in the same side of a separating multicurve
![]() $m$
if and only if
$m$
if and only if
![]() $\alpha (a)$
and
$\alpha (a)$
and
![]() $\alpha (b)$
lie in the same side of
$\alpha (b)$
lie in the same side of
![]() $\alpha (m)$
.
$\alpha (m)$
.
Note that Lemma 3.3 states that a curve
![]() $c$
is separating if (and only if)
$c$
is separating if (and only if)
![]() $\alpha (c)$
is separating. Here, we review the following notions from graph theory:
$\alpha (c)$
is separating. Here, we review the following notions from graph theory:
-
• A graph is a join if its vertices are divided into two or more nonempty sets such that each vertex in one of the sets is connected by an edge to every vertex in the other sets.
-
• The link of a set
 $A$
of vertices in a graph is the subgraph spanned by the set of vertices that are not in
$A$
of vertices in a graph is the subgraph spanned by the set of vertices that are not in
 $A$
and are connected by an edge to each vertex in
$A$
and are connected by an edge to each vertex in
 $A$
.
$A$
.
For example, for
![]() $c,d_1,\dots, d_k \in \mathcal{C}^{\dagger }(F)$
,
$c,d_1,\dots, d_k \in \mathcal{C}^{\dagger }(F)$
,
![]() $c$
is a vertex of the link of
$c$
is a vertex of the link of
![]() $\{d_1,\dots, d_k\}$
in
$\{d_1,\dots, d_k\}$
in
![]() $\mathcal{C}^{\dagger }(F)$
if and only if
$\mathcal{C}^{\dagger }(F)$
if and only if
![]() $c$
and
$c$
and
![]() $d_i$
are disjoint curves in
$d_i$
are disjoint curves in
![]() $F$
for each
$F$
for each
![]() $i=1,\dots, k$
.
$i=1,\dots, k$
.
Lemma 3.3 can be proved as in [Reference Long, Margalit, Pham, Verberne and Yao5] in the following way. We can observe that a multicurve
![]() $m$
is separating if and only if the link of
$m$
is separating if and only if the link of
![]() $m$
is a join; this shows the former claim. The latter claim follows from the fact that two curves lie in the same side of
$m$
is a join; this shows the former claim. The latter claim follows from the fact that two curves lie in the same side of
![]() $m$
if and only if they belong to the same set in the partition of the link of
$m$
if and only if they belong to the same set in the partition of the link of
![]() $m$
as a join.
$m$
as a join.
We define the hull of a collection of curves in a surface to be the union of the curves along with any embedded disks bounded by the curves.
Lemma 3.4 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 2.4]). Let
![]() $N=N_{{g}}$
with
$N=N_{{g}}$
with
![]() ${g} \geq 2$
, let
${g} \geq 2$
, let
![]() $X$
be a finite set of vertices represented by two-sided curves in
$X$
be a finite set of vertices represented by two-sided curves in
![]() $N$
of
$N$
of
![]() $\mathcal{C}^{\dagger }(N)$
, and let
$\mathcal{C}^{\dagger }(N)$
, and let
![]() $d$
be a vertex of
$d$
be a vertex of
![]() $\mathcal{C}^{\dagger }(N)$
. Then,
$\mathcal{C}^{\dagger }(N)$
. Then,
![]() $d$
lies in the hull of
$d$
lies in the hull of
![]() $X$
if and only if the link of
$X$
if and only if the link of
![]() $d$
contains the link of
$d$
contains the link of
![]() $X$
. In particular, if
$X$
. In particular, if
![]() $d$
lies in the hull of
$d$
lies in the hull of
![]() $X$
, then
$X$
, then
![]() $\alpha (d)$
lies in the hull of
$\alpha (d)$
lies in the hull of
![]() $\alpha (X)$
for every
$\alpha (X)$
for every
![]() $\alpha \in \mathrm{Aut}(\mathcal{C}^{\dagger }(N))$
.
$\alpha \in \mathrm{Aut}(\mathcal{C}^{\dagger }(N))$
.
Note that we assume that
![]() $X$
consists only of two-sided curves in Lemma 3.4. With this restriction, we can prove Lemma 3.4 in the same way as in [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 2.4]. We include a proof of Lemma 3.4 to explain why we added such a restriction.
$X$
consists only of two-sided curves in Lemma 3.4. With this restriction, we can prove Lemma 3.4 in the same way as in [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 2.4]. We include a proof of Lemma 3.4 to explain why we added such a restriction.
Proof of Lemma 3.4. For the forward direction, suppose that
![]() $d$
is a vertex of
$d$
is a vertex of
![]() $\mathcal{C}^{\dagger }(N)$
that lies in the hull of
$\mathcal{C}^{\dagger }(N)$
that lies in the hull of
![]() $X$
. We assume that there exists a vertex
$X$
. We assume that there exists a vertex
![]() $e$
of
$e$
of
![]() $\mathcal{C}^{\dagger }(N)$
which intersects
$\mathcal{C}^{\dagger }(N)$
which intersects
![]() $d$
but is disjoint from each curve in
$d$
but is disjoint from each curve in
![]() $X$
. Then,
$X$
. Then,
![]() $e$
should be contained in
$e$
should be contained in
![]() $N\setminus X$
. Since
$N\setminus X$
. Since
![]() $d$
lies in the hull of
$d$
lies in the hull of
![]() $X$
and
$X$
and
![]() $e$
intersects with
$e$
intersects with
![]() $d$
, the curve
$d$
, the curve
![]() $e$
should be contained in a connected component of
$e$
should be contained in a connected component of
![]() $N\setminus X$
which is a disk. Then it follows that
$N\setminus X$
which is a disk. Then it follows that
![]() $e$
is an inessential curve bounding a disk. This contradicts the assumption that
$e$
is an inessential curve bounding a disk. This contradicts the assumption that
![]() $e$
is a vertex of
$e$
is a vertex of
![]() $\mathcal{C}^{\dagger }(N)$
.
$\mathcal{C}^{\dagger }(N)$
.
For the other direction, suppose that
![]() $d$
is a vertex of
$d$
is a vertex of
![]() $\mathcal{C}^{\dagger }(N)$
that does not lie in the hull of
$\mathcal{C}^{\dagger }(N)$
that does not lie in the hull of
![]() $X$
(i.e.,
$X$
(i.e.,
![]() $d$
is not a vertex of
$d$
is not a vertex of
![]() $X$
nor a curve that lies in the union of disks bounding the curves in
$X$
nor a curve that lies in the union of disks bounding the curves in
![]() $X$
). This means that there is a component of
$X$
). This means that there is a component of
![]() $d\setminus X$
which lies in a component
$d\setminus X$
which lies in a component
![]() $R$
of
$R$
of
![]() $N\setminus X$
that is not a disk. If the genus (as either orientable or nonorientable surface) of
$N\setminus X$
that is not a disk. If the genus (as either orientable or nonorientable surface) of
![]() $R$
is at least
$R$
is at least
![]() $1$
, it is clear that there exists a curve in
$1$
, it is clear that there exists a curve in
![]() $R$
which is essential in
$R$
which is essential in
![]() $N$
. If the genus of
$N$
. If the genus of
![]() $R$
is
$R$
is
![]() $0$
, then each curve in
$0$
, then each curve in
![]() $R$
parallel to a boundary component of
$R$
parallel to a boundary component of
![]() $R$
is an essential curve (here we use two-sidedness of the curves corresponding to the vertices of
$R$
is an essential curve (here we use two-sidedness of the curves corresponding to the vertices of
![]() $X$
). In particular,
$X$
). In particular,
![]() $R$
contains an essential curve in
$R$
contains an essential curve in
![]() $N$
which intersects
$N$
which intersects
![]() $d$
, as desired.
$d$
, as desired.
Remark 3.5. In Lemma 3.4, the set
![]() $X$
should consist only of two-sided curves in
$X$
should consist only of two-sided curves in
![]() $N$
; if we allow one-sided curves, then the proof of Lemma 3.4 will not work. More specifically, if
$N$
; if we allow one-sided curves, then the proof of Lemma 3.4 will not work. More specifically, if
![]() $X$
contains a one-sided curve
$X$
contains a one-sided curve
![]() $c$
and the genus of
$c$
and the genus of
![]() $R$
in the proof of Lemma 3.4 is
$R$
in the proof of Lemma 3.4 is
![]() $0$
, then there is the boundary component
$0$
, then there is the boundary component
![]() $\partial _{c}$
of
$\partial _{c}$
of
![]() $N\setminus X$
corresponding to
$N\setminus X$
corresponding to
![]() $c$
. Thus, a curve in
$c$
. Thus, a curve in
![]() $R$
parallel to
$R$
parallel to
![]() $\partial _{c}$
bounds a Möbius band in
$\partial _{c}$
bounds a Möbius band in
![]() $N$
, which is not essential in
$N$
, which is not essential in
![]() $N$
.
$N$
.
Lemma 3.6. Let
![]() $N=N_{{g}}$
with
$N=N_{{g}}$
with
![]() ${g} \geq 4$
, let
${g} \geq 4$
, let
![]() $\alpha$
be an automorphism of
$\alpha$
be an automorphism of
![]() $\mathcal{C}^{\dagger }(N)$
, and let
$\mathcal{C}^{\dagger }(N)$
, and let
![]() $c$
be a curve in
$c$
be a curve in
![]() $N$
. If
$N$
. If
![]() $c$
is one-sided
$c$
is one-sided
![]() $($
resp. two-sided
$($
resp. two-sided
![]() $)$
, then
$)$
, then
![]() $\alpha (c)$
is also one-sided
$\alpha (c)$
is also one-sided
![]() $($
resp. two-sided
$($
resp. two-sided
![]() $)$
.
$)$
.
Proof. Assume that
![]() $c$
is one-sided. Then
$c$
is one-sided. Then
![]() $c$
is nonseparating. We prove that
$c$
is nonseparating. We prove that
![]() $\alpha (c)$
is also one-sided. By Lemma 3.3,
$\alpha (c)$
is also one-sided. By Lemma 3.3,
![]() $\alpha (c)$
is also nonseparating. Let
$\alpha (c)$
is also nonseparating. Let
![]() $F$
and
$F$
and
![]() $F'$
be surfaces obtained by cutting
$F'$
be surfaces obtained by cutting
![]() $N_{g}$
along
$N_{g}$
along
![]() $c$
and
$c$
and
![]() $\alpha (c)$
, respectively.
$\alpha (c)$
, respectively.
If
![]() $F$
is orientable, then
$F$
is orientable, then
![]() $F$
is homeomorphic to
$F$
is homeomorphic to
![]() $S^1_{\frac{{g}-1}{2}}$
. Assume that
$S^1_{\frac{{g}-1}{2}}$
. Assume that
![]() $\alpha (c)$
is two-sided. Then
$\alpha (c)$
is two-sided. Then
![]() $F'$
is homeomorphic to
$F'$
is homeomorphic to
![]() $N^2_{{g}-2}$
since
$N^2_{{g}-2}$
since
![]() $g$
is odd. Thus, we can take a nonseparating multicurve
$g$
is odd. Thus, we can take a nonseparating multicurve
![]() $\{d_1,\cdots, d_{{g}-2}\}$
in
$\{d_1,\cdots, d_{{g}-2}\}$
in
![]() $F'$
. This implies that
$F'$
. This implies that
![]() $\{\alpha (c),d_1,\cdots, d_{{g} -2}\}$
is a nonseparating multicurve in
$\{\alpha (c),d_1,\cdots, d_{{g} -2}\}$
is a nonseparating multicurve in
![]() $N_{g}$
. By Lemma 3.3,
$N_{g}$
. By Lemma 3.3,
![]() $\{c,\alpha ^{-1}(d_1),\cdots, \alpha ^{-1}(d_{{g}-2})\}$
is also a nonseparating multicurve in
$\{c,\alpha ^{-1}(d_1),\cdots, \alpha ^{-1}(d_{{g}-2})\}$
is also a nonseparating multicurve in
![]() $N_{g}$
, and it implies that
$N_{g}$
, and it implies that
![]() $F$
admits a nonseparating multicurve
$F$
admits a nonseparating multicurve
![]() $\{\alpha ^{-1}(d_1),\cdots, \alpha ^{-1}(d_{{g}-2})\}$
consisting of
$\{\alpha ^{-1}(d_1),\cdots, \alpha ^{-1}(d_{{g}-2})\}$
consisting of
![]() $({g} -2)$
curves. Hence, we obtain
$({g} -2)$
curves. Hence, we obtain
![]() $\frac{{g}-1}{2} \geq{g}-2$
, but this contradicts the assumption that
$\frac{{g}-1}{2} \geq{g}-2$
, but this contradicts the assumption that
![]() ${g} \geq 4$
. Therefore, we see that
${g} \geq 4$
. Therefore, we see that
![]() $\alpha (c)$
is one-sided.
$\alpha (c)$
is one-sided.
If
![]() $F$
is nonorientable, then
$F$
is nonorientable, then
![]() $F$
is homeomorphic to
$F$
is homeomorphic to
![]() $N_{{g}-1}^1$
. Thus, we can take a nonseparating multicurve
$N_{{g}-1}^1$
. Thus, we can take a nonseparating multicurve
![]() $\{d_1,\cdots, d_{{g}-1}\}$
in
$\{d_1,\cdots, d_{{g}-1}\}$
in
![]() $F$
. We can see that
$F$
. We can see that
![]() $F'$
admits a nonseparating multicurve consisting of
$F'$
admits a nonseparating multicurve consisting of
![]() $({g}-1)$
curves by the same argument as above. Hence, the genus of
$({g}-1)$
curves by the same argument as above. Hence, the genus of
![]() $F'$
is
$F'$
is
![]() $({g}-1)$
, and therefore
$({g}-1)$
, and therefore
![]() $\alpha (c)$
is one-sided by Lemma 2.1.
$\alpha (c)$
is one-sided by Lemma 2.1.
If
![]() $\alpha (c)$
is one-sided, then
$\alpha (c)$
is one-sided, then
![]() $c=\alpha ^{-1}(\alpha (c))$
is also one-sided. By contraposition, if
$c=\alpha ^{-1}(\alpha (c))$
is also one-sided. By contraposition, if
![]() $c$
is two-sided, then
$c$
is two-sided, then
![]() $\alpha (c)$
is also two-sided.
$\alpha (c)$
is also two-sided.
Lemma 3.7 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 2.5]). Let
![]() $N=N_{g}$
with
$N=N_{g}$
with
![]() $g\geq 4$
. Then every automorphism
$g\geq 4$
. Then every automorphism
![]() $\alpha$
of
$\alpha$
of
![]() $\mathcal{C}^{\dagger }(N)$
preserves
$\mathcal{C}^{\dagger }(N)$
preserves
-
• the set of torus pairs,
-
• the set of degenerate torus pairs,
-
• the set of nondegenerate torus pairs, and
-
• the set of torus triples.
Proof. As in the case of orientable surfaces [Reference Long, Margalit, Pham, Verberne and Yao5], we proceed Lemma 3.7 in four steps:
-
1.
 $\alpha$
preserves the union of torus pairs and pants pairs consisting of only nonseparating curves
$\alpha$
preserves the union of torus pairs and pants pairs consisting of only nonseparating curves -
2.
 $\alpha$
preserves the set of torus pairs
$\alpha$
preserves the set of torus pairs -
3.
 $\alpha$
preserves the degenerate torus pairs
$\alpha$
preserves the degenerate torus pairs -
4.
 $\alpha$
preserves the set of torus triples
$\alpha$
preserves the set of torus triples
Step 1. Let
![]() $c$
and
$c$
and
![]() $d$
be nonseparating two-sided curves that intersect. It is enough to show that the following three conditions are equivalent:
$d$
be nonseparating two-sided curves that intersect. It is enough to show that the following three conditions are equivalent:
-
(1) The pair
 $\{c,d\}$
is a torus pair or a pants pair.
$\{c,d\}$
is a torus pair or a pants pair. -
(2) There exists at most one other vertex of
 $\mathcal{C}^{\dagger }(N)$
that lies in the hull of
$\mathcal{C}^{\dagger }(N)$
that lies in the hull of
 $\{c,d\}$
.
$\{c,d\}$
. -
(3) There exists at most one vertex of
 $\mathcal{C}^{\dagger }(N)$
whose link contains the link of
$\mathcal{C}^{\dagger }(N)$
whose link contains the link of
 $\{c,d\}$
.
$\{c,d\}$
.
Items (2) and (3) are equivalent by Lemma 3.4. Item (1) implies (2) since if
![]() $\{c,d\}$
is a torus pair or a pants pair, then its hull is
$\{c,d\}$
is a torus pair or a pants pair, then its hull is
![]() $c \cup d$
. Now we prove that (2) does not hold if (1) does not (this means that (2) implies (1)).
$c \cup d$
. Now we prove that (2) does not hold if (1) does not (this means that (2) implies (1)).
We modify the argument in [Reference Long, Margalit, Pham, Verberne and Yao5]. Assume that (1) does not hold (i.e.,
![]() $\{c, d\}$
is neither a torus pair nor a pants pair). If
$\{c, d\}$
is neither a torus pair nor a pants pair). If
![]() $\{c, d\}$
is a bigon pair, then the hull of
$\{c, d\}$
is a bigon pair, then the hull of
![]() $\{c, d\}$
admits infinitely many vertices, which means that (2) does not hold. Thus, it is sufficient to consider the case where
$\{c, d\}$
admits infinitely many vertices, which means that (2) does not hold. Thus, it is sufficient to consider the case where
![]() $\{c, d\}$
is not a bigon pair. Then,
$\{c, d\}$
is not a bigon pair. Then,
![]() $c \cap d$
has two distinct connected components, say
$c \cap d$
has two distinct connected components, say
![]() $a_1$
and
$a_1$
and
![]() $a_2$
. They divide
$a_2$
. They divide
![]() $c$
into two curves
$c$
into two curves
![]() $c_1$
and
$c_1$
and
![]() $c_2$
:
$c_2$
:
![]() $c \setminus (a_1 \sqcup a_2) = c_1 \sqcup c_2$
. Similarly, they also divide
$c \setminus (a_1 \sqcup a_2) = c_1 \sqcup c_2$
. Similarly, they also divide
![]() $d$
into
$d$
into
![]() $d_1$
and
$d_1$
and
![]() $d_2$
We can take
$d_2$
We can take
![]() $a_1$
and
$a_1$
and
![]() $a_2$
so that
$a_2$
so that
![]() $c \cap d_1 = \emptyset$
(e.g., if we consider a moving point on
$c \cap d_1 = \emptyset$
(e.g., if we consider a moving point on
![]() $d$
starting from a component
$d$
starting from a component
![]() $a_1$
, we can take
$a_1$
, we can take
![]() $a_2$
as the component where the point hits
$a_2$
as the component where the point hits
![]() $c$
for the first time). We also take two distinct connected components
$c$
for the first time). We also take two distinct connected components
![]() $b_1$
and
$b_1$
and
![]() $b_2$
of
$b_2$
of
![]() $c \cap d$
with
$c \cap d$
with
![]() $a_1 \neq b_1$
(it could be
$a_1 \neq b_1$
(it could be
![]() $a_1 = b_2$
or
$a_1 = b_2$
or
![]() $a_2 = b_1$
). They divide
$a_2 = b_1$
). They divide
![]() $c$
into
$c$
into
![]() $c'_1,c'_2$
and divide
$c'_1,c'_2$
and divide
![]() $d$
into
$d$
into
![]() $d'_1,d'_2$
. We can take
$d'_1,d'_2$
. We can take
![]() $b_1$
and
$b_1$
and
![]() $b_2$
to satisfy that
$b_2$
to satisfy that
![]() $c'_1 \cap d = \emptyset$
and
$c'_1 \cap d = \emptyset$
and
![]() $c'_1 \neq c_1$
(we can choose
$c'_1 \neq c_1$
(we can choose
![]() $c'_1 = c_2$
if
$c'_1 = c_2$
if
![]() $a_1 = b_2$
and
$a_1 = b_2$
and
![]() $a_2 = b_1$
). In
$a_2 = b_1$
). In
![]() $c \cup d$
, there are four distinct simple closed curves
$c \cup d$
, there are four distinct simple closed curves
![]() $e_1$
,
$e_1$
,
![]() $e_2$
,
$e_2$
,
![]() $e_3$
, and
$e_3$
, and
![]() $e_4$
that contain
$e_4$
that contain
![]() $c_1 \cup d_1$
,
$c_1 \cup d_1$
,
![]() $c_2 \cup d_1$
,
$c_2 \cup d_1$
,
![]() $c'_1 \cup d'_1$
, and
$c'_1 \cup d'_1$
, and
![]() $c'_2 \cup d'_1$
, respectively; they are all distinct from both
$c'_2 \cup d'_1$
, respectively; they are all distinct from both
![]() $c$
and
$c$
and
![]() $d$
.
$d$
.
If we assume that (2) holds (for contradiction), then the following holds: at least one of the pairs
![]() $\{e_1,e_2\}$
and
$\{e_1,e_2\}$
and
![]() $\{e_3,e_4\}$
consists only of inessential curves. Let
$\{e_3,e_4\}$
consists only of inessential curves. Let
![]() $e_1$
and
$e_1$
and
![]() $e_2$
be inessential without loss of generality. Then, we observe contradictions as follows:
$e_2$
be inessential without loss of generality. Then, we observe contradictions as follows:
-
• If
 $e_1$
or
$e_1$
or
 $e_2$
bounds a disk, then the hull of
$e_2$
bounds a disk, then the hull of
 $\{c,d\}$
contains infinitely many distinct curves; this contradicts the assumption that (2) holds.
$\{c,d\}$
contains infinitely many distinct curves; this contradicts the assumption that (2) holds. -
• If both
 $e_1$
and
$e_1$
and
 $e_2$
bound a Möbius band, then they represent the same homology class
$e_2$
bound a Möbius band, then they represent the same homology class
 $[e_1]=[e_2]$
of
$[e_1]=[e_2]$
of
 $H_1(N,\mathbb{Z}/2\mathbb{Z})$
. Then
$H_1(N,\mathbb{Z}/2\mathbb{Z})$
. Then
 $[c]=[e_1]+[e_2] = 0$
in
$[c]=[e_1]+[e_2] = 0$
in
 $H_1(N,\mathbb{Z}/2\mathbb{Z})$
; this means that
$H_1(N,\mathbb{Z}/2\mathbb{Z})$
; this means that
 $c$
is separating, which contradicts the assumption that
$c$
is separating, which contradicts the assumption that
 $c$
is nonseparating.
$c$
is nonseparating.
Therefore, we have finished the proof of Step 1.
Step 2. By Lemma 3.3, it suffices to prove the following. Let
![]() $c$
and
$c$
and
![]() $d$
be nonseparating two-sided curves that form a torus pair or a pants pair. Then, the pair
$d$
be nonseparating two-sided curves that form a torus pair or a pants pair. Then, the pair
![]() $\{c,d\}$
is a torus pair if and only if there exists a separating curve
$\{c,d\}$
is a torus pair if and only if there exists a separating curve
![]() $e$
which is disjoint from both
$e$
which is disjoint from both
![]() $c$
and
$c$
and
![]() $d$
, and all nonseparating simple closed curves in
$d$
, and all nonseparating simple closed curves in
![]() $N$
lying in the same side of
$N$
lying in the same side of
![]() $e$
as
$e$
as
![]() $\{c,d\}$
intersect
$\{c,d\}$
intersect
![]() $c\cup d$
. We now follow the proof of [Reference Long, Margalit, Pham, Verberne and Yao5, Step 2 in Lemma 2.5].
$c\cup d$
. We now follow the proof of [Reference Long, Margalit, Pham, Verberne and Yao5, Step 2 in Lemma 2.5].
Let
![]() $\{c,d\}$
be a torus pair (then both
$\{c,d\}$
be a torus pair (then both
![]() $c$
and
$c$
and
![]() $d$
are nonseparating by definition). Let
$d$
are nonseparating by definition). Let
![]() $R$
be a neighborhood of
$R$
be a neighborhood of
![]() $c\cup d$
which is homotopic to a torus with one boundary component
$c\cup d$
which is homotopic to a torus with one boundary component
![]() $e$
(here, we use the two-sidedness of torus pairs). The resulting surface by cutting
$e$
(here, we use the two-sidedness of torus pairs). The resulting surface by cutting
![]() $R$
along
$R$
along
![]() $c\cup d$
is an annulus. Any nonseparating curve in
$c\cup d$
is an annulus. Any nonseparating curve in
![]() $R$
is not homotopic to
$R$
is not homotopic to
![]() $e$
. Hence, any nonseparating curve in
$e$
. Hence, any nonseparating curve in
![]() $R$
intersects with
$R$
intersects with
![]() $c\cup d$
. For the other direction, we assume that
$c\cup d$
. For the other direction, we assume that
![]() $c$
and
$c$
and
![]() $d$
are nonseparating two-sided curves in
$d$
are nonseparating two-sided curves in
![]() $N$
forming a pants pair
$N$
forming a pants pair
![]() $\{c,d\}$
. Let
$\{c,d\}$
. Let
![]() $e$
be any separating curve which is disjoint from
$e$
be any separating curve which is disjoint from
![]() $c\cup d$
, and let
$c\cup d$
, and let
![]() $R$
be the subsurface of
$R$
be the subsurface of
![]() $N$
that contains
$N$
that contains
![]() $c\cup d$
and has boundary
$c\cup d$
and has boundary
![]() $e$
. Then,
$e$
. Then,
![]() $R$
needs to have a positive genus since
$R$
needs to have a positive genus since
![]() $N$
is closed and
$N$
is closed and
![]() $c$
and
$c$
and
![]() $d$
are not homotopic. There exists a closed neighborhood of
$d$
are not homotopic. There exists a closed neighborhood of
![]() $c\cup d$
which is a pair of pants
$c\cup d$
which is a pair of pants
![]() $P$
contained in
$P$
contained in
![]() $R$
. We let
$R$
. We let
![]() $P^{\circ }$
denote the interior of
$P^{\circ }$
denote the interior of
![]() $P$
. Since the genus of
$P$
. Since the genus of
![]() $P$
is
$P$
is
![]() $0$
, there exists a curve in
$0$
, there exists a curve in
![]() $R\setminus P^{\circ }$
that is nonseparating in
$R\setminus P^{\circ }$
that is nonseparating in
![]() $R$
(and hence in
$R$
(and hence in
![]() $N$
). This completes the proof of Step 2.
$N$
). This completes the proof of Step 2.
Step 3 and Step 4 can be proved as in [Reference Long, Margalit, Pham, Verberne and Yao5] as follows, and thus we obtain Lemma 3.7. We can observe that a torus pair
![]() $\{c,d\}$
is nondegenerate if and only if there is exactly one other vertex of
$\{c,d\}$
is nondegenerate if and only if there is exactly one other vertex of
![]() $\mathcal{C}^{\dagger }(N)$
in the hull of
$\mathcal{C}^{\dagger }(N)$
in the hull of
![]() $\{c,d\}$
; Step 3 follows from this observation and Lemma 3.4. Step 4 follows from Step 2, Lemma 3.4 and the fact that if
$\{c,d\}$
; Step 3 follows from this observation and Lemma 3.4. Step 4 follows from Step 2, Lemma 3.4 and the fact that if
![]() $\{c,d,e\}$
is a torus triple, then
$\{c,d,e\}$
is a torus triple, then
![]() $e$
is the exactly one other vertex in the hull of
$e$
is the exactly one other vertex in the hull of
![]() $\{c,d\}$
.
$\{c,d\}$
.
Remark 3.8. We summarize here the issues and their solutions in considering nonorientable surfaces in the proof of Lemma 3.7.
-
1. Since we impose two-sidedness on torus pairs and pants pairs, we need Lemma 3.6 to deduce the conclusion from (1)–(3) in Step 1.
-
2. In Step 1 of the proof of Lemma 3.7, we argued under the assumption that torus pairs and pants pairs consist only of nonseparating curves, which is not needed for the case of orientable surfaces [Reference Long, Margalit, Pham, Verberne and Yao5]. Without that assumption, if we attempt to make the same argument as in the orientable case, we have the following issue. In [Reference Long, Margalit, Pham, Verberne and Yao5], they used the fact that any inessential curve of orientable surfaces bounds a disk, and so if at least one curve in
 $\{e_{1},e_{2}, e_{3}, e_{4}\}$
is inessential, then it follows that the hull of
$\{e_{1},e_{2}, e_{3}, e_{4}\}$
is inessential, then it follows that the hull of
 $\{c,d\}$
contains infinitely many distinct essential curves other than
$\{c,d\}$
contains infinitely many distinct essential curves other than
 $c$
and
$c$
and
 $d$
. However, for nonorientable surfaces, the curves bounding a Möbius band are also inessential. Then we have the case where the hull of
$d$
. However, for nonorientable surfaces, the curves bounding a Möbius band are also inessential. Then we have the case where the hull of
 $\{c,d\}$
contains at most one essential curve other than
$\{c,d\}$
contains at most one essential curve other than
 $c$
and
$c$
and
 $d$
, but
$d$
, but
 $\{c,d\}$
does not form a torus pair nor a pants pair if we allow
$\{c,d\}$
does not form a torus pair nor a pants pair if we allow
 $c$
or
$c$
or
 $d$
to be separating.
$d$
to be separating. -
3. The reason why we consider only two-sided curves for torus pairs/triples is as follows: if both
 $c$
and
$c$
and
 $d$
are one-sided curves in Step 2, the curve
$d$
are one-sided curves in Step 2, the curve
 $e$
may not be separating by taking a boundary curve of
$e$
may not be separating by taking a boundary curve of
 $R$
.
$R$
.
We explain the definition of an annulus set. Suppose that
![]() $(a,b)$
is an ordered pair of vertices of
$(a,b)$
is an ordered pair of vertices of
![]() $\mathcal{C}^{\dagger }(N)$
that are disjoint, homotopic two-sided curves. Assuming
$\mathcal{C}^{\dagger }(N)$
that are disjoint, homotopic two-sided curves. Assuming
![]() ${g} \geq 3$
, there is a unique annulus
${g} \geq 3$
, there is a unique annulus
![]() $A$
in
$A$
in
![]() $N_{{g}}$
whose boundary is
$N_{{g}}$
whose boundary is
![]() $a\cup b$
. Let
$a\cup b$
. Let
![]() $\mathcal{C}^{\dagger }(a,b)$
be the set of vertices of
$\mathcal{C}^{\dagger }(a,b)$
be the set of vertices of
![]() $\mathcal{C}^{\dagger }(N_{{g}})$
consisting of curves contained in the interior of
$\mathcal{C}^{\dagger }(N_{{g}})$
consisting of curves contained in the interior of
![]() $A$
. We refer to
$A$
. We refer to
![]() $\mathcal{C}^{\dagger }(a,b)$
as an annulus set. We call a pair of vertices of
$\mathcal{C}^{\dagger }(a,b)$
as an annulus set. We call a pair of vertices of
![]() $\mathcal{C}^{\dagger }(N_{g})$
is an annulus pair if they lie in some annulus set
$\mathcal{C}^{\dagger }(N_{g})$
is an annulus pair if they lie in some annulus set
![]() $\mathcal{C}^{\dagger }(a,b)$
. A nonseparating noncrossing annulus pair is an annulus pair where both curves are nonseparating and the curves are noncrossing. There is a natural partial ordering on the annulus set
$\mathcal{C}^{\dagger }(a,b)$
. A nonseparating noncrossing annulus pair is an annulus pair where both curves are nonseparating and the curves are noncrossing. There is a natural partial ordering on the annulus set
![]() $\mathcal{C}^{\dagger }(a,b)$
: we say that
$\mathcal{C}^{\dagger }(a,b)$
: we say that
![]() $c\preceq d$
if
$c\preceq d$
if
![]() $c$
and
$c$
and
![]() $d$
are noncrossing and each component of
$d$
are noncrossing and each component of
![]() $c\setminus d$
lies in the component of
$c\setminus d$
lies in the component of
![]() $A\setminus d$
bounded by
$A\setminus d$
bounded by
![]() $a$
.
$a$
.
Lemma 3.9 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 2.6]). Let
![]() $N=N_{g}$
with
$N=N_{g}$
with
![]() $g\geq 4$
, let
$g\geq 4$
, let
![]() $\alpha$
be an automorphism of
$\alpha$
be an automorphism of
![]() $\mathcal{C}^{\dagger }(N)$
, and let
$\mathcal{C}^{\dagger }(N)$
, and let
![]() $a$
and
$a$
and
![]() $b$
be disjoint, homotopic nonseparating two-sided curves. Then,
$b$
be disjoint, homotopic nonseparating two-sided curves. Then,
-
(1) the curves
 $\alpha (a)$
and
$\alpha (a)$
and
 $\alpha (b)$
are disjoint, homotopic nonseparating two-sided curves,
$\alpha (b)$
are disjoint, homotopic nonseparating two-sided curves, -
(2) the image of
 $\mathcal{C}^{\dagger }(a,b)$
under
$\mathcal{C}^{\dagger }(a,b)$
under
 $\alpha$
is
$\alpha$
is
 $\mathcal{C}^{\dagger }(\alpha (a), \alpha (b))$
,
$\mathcal{C}^{\dagger }(\alpha (a), \alpha (b))$
, -
(3) if
 $c,d\in \mathcal{C}^{\dagger }(a,b)$
are noncrossing then
$c,d\in \mathcal{C}^{\dagger }(a,b)$
are noncrossing then
 $\alpha (c)$
and
$\alpha (c)$
and
 $\alpha (d)$
are noncrossing, and
$\alpha (d)$
are noncrossing, and -
(4) if
 $c\preceq d$
in
$c\preceq d$
in
 $\mathcal{C}^{\dagger }(a,b)$
, then
$\mathcal{C}^{\dagger }(a,b)$
, then
 $\alpha (c)\preceq \alpha (d)$
in
$\alpha (c)\preceq \alpha (d)$
in
 $\mathcal{C}^{\dagger }(\alpha (a), \alpha (b))$
.
$\mathcal{C}^{\dagger }(\alpha (a), \alpha (b))$
.
Note that if two curves
![]() $a$
and
$a$
and
![]() $b$
on
$b$
on
![]() $N$
are disjoint and homotopic, then it automatically follows that
$N$
are disjoint and homotopic, then it automatically follows that
![]() $a$
and
$a$
and
![]() $b$
are two-sided since any pair of homotopic one-sided curves must intersect.
$b$
are two-sided since any pair of homotopic one-sided curves must intersect.
Proof of Lemma 3.9. For two disjoint nonseparating two-sided curves
![]() $a,b$
such that
$a,b$
such that
![]() $\{a,b\}$
is a separating multicurve, we can observe, by Lemma 2.2, that the following two conditions are equivalent:
$\{a,b\}$
is a separating multicurve, we can observe, by Lemma 2.2, that the following two conditions are equivalent:
-
• At least one component of the surface obtained by cutting
 $N_{g}$
along
$N_{g}$
along
 $a$
and
$a$
and
 $b$
is homeomorphic to
$b$
is homeomorphic to
 $S_0^2$
or
$S_0^2$
or
 $N_1^2$
.
$N_1^2$
. -
• All separating curves disjoint from
 $a$
and
$a$
and
 $b$
lie in the same side of
$b$
lie in the same side of
 $\{a,b\}$
(if they exist).
$\{a,b\}$
(if they exist).
Let
![]() $F$
and
$F$
and
![]() $F'$
(resp.
$F'$
(resp.
![]() $\tilde{F}$
and
$\tilde{F}$
and
![]() $\tilde{F}'$
) denote the connected components of the surface obtained from
$\tilde{F}'$
) denote the connected components of the surface obtained from
![]() $N_{g}$
by cutting along
$N_{g}$
by cutting along
![]() $a$
and
$a$
and
![]() $b$
(resp.
$b$
(resp.
![]() $\alpha (a)$
and
$\alpha (a)$
and
![]() $\alpha (b)$
). Since
$\alpha (b)$
). Since
![]() $a$
and
$a$
and
![]() $b$
are homotopic, we can assume that
$b$
are homotopic, we can assume that
![]() $F \cong S_0^2$
and
$F \cong S_0^2$
and
![]() $F' \cong N_{{g}-2}^2$
. By Lemma 3.3 and the above observation,
$F' \cong N_{{g}-2}^2$
. By Lemma 3.3 and the above observation,
![]() $\tilde{F} \sqcup \tilde{F}'$
is homeomorphic to
$\tilde{F} \sqcup \tilde{F}'$
is homeomorphic to
![]() $S_0^2 \sqcup N_{{g}-2}^2$
or
$S_0^2 \sqcup N_{{g}-2}^2$
or
![]() $N_1^2\sqcup N_{{g}-3}^2$
. Now we assume that the latter holds (to derive a contradiction). We assume that
$N_1^2\sqcup N_{{g}-3}^2$
. Now we assume that the latter holds (to derive a contradiction). We assume that
![]() $\tilde{F} \cong N_1^2$
. Take a one-sided curve
$\tilde{F} \cong N_1^2$
. Take a one-sided curve
![]() $c$
lies in
$c$
lies in
![]() $\tilde{F}$
. Since
$\tilde{F}$
. Since
![]() $\alpha ^{-1}(c)$
is one-sided by Lemma 3.6, the curve
$\alpha ^{-1}(c)$
is one-sided by Lemma 3.6, the curve
![]() $\alpha ^{-1}(c)$
must lie in
$\alpha ^{-1}(c)$
must lie in
![]() $F'$
. If we take a separating essential curve
$F'$
. If we take a separating essential curve
![]() $d$
that lies in
$d$
that lies in
![]() $F'$
(it exists since
$F'$
(it exists since
![]() ${g} \geq 4$
), then
${g} \geq 4$
), then
![]() $\alpha (d)$
is separating and lies in
$\alpha (d)$
is separating and lies in
![]() $\tilde{F}$
by Lemma 3.3. This contradicts Lemma 2.2 and hence (1) follows.
$\tilde{F}$
by Lemma 3.3. This contradicts Lemma 2.2 and hence (1) follows.
Item (2) follows from (1) and Lemma 3.3. In (3) and (4), we discuss in an annular domain, and it does not depend on the orientability of the surface. Therefore, they are shown by exactly the same arguments as in [Reference Long, Margalit, Pham, Verberne and Yao5], so we omit their proofs.
Now we define type 1 and type 2 curves. Suppose that
![]() $\{c,d\}$
is a nonseparating noncrossing annulus pair, and suppose that
$\{c,d\}$
is a nonseparating noncrossing annulus pair, and suppose that
![]() $e$
is a curve so that
$e$
is a curve so that
![]() $\{c,e\}$
and
$\{c,e\}$
and
![]() $\{d, e\}$
are degenerate torus pairs. If
$\{d, e\}$
are degenerate torus pairs. If
![]() $c\cap e$
and
$c\cap e$
and
![]() $d\cap e$
are the same point, then we say that
$d\cap e$
are the same point, then we say that
![]() $e$
is a type 1 curve for
$e$
is a type 1 curve for
![]() $\{c,d\}$
. Otherwise, we say that
$\{c,d\}$
. Otherwise, we say that
![]() $e$
is a type 2 curve for
$e$
is a type 2 curve for
![]() $\{c,d\}$
.
$\{c,d\}$
.
Lemma 3.10 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 2.7]). Let
![]() $N=N_{g}$
with
$N=N_{g}$
with
![]() $g\geq 3$
. Then every automorphism
$g\geq 3$
. Then every automorphism
![]() $\alpha$
of
$\alpha$
of
![]() $\mathcal{C}^{\dagger }(N)$
preserves type 1 and type 2 curves for nonseparating noncrossing annulus pairs. More precisely, if
$\mathcal{C}^{\dagger }(N)$
preserves type 1 and type 2 curves for nonseparating noncrossing annulus pairs. More precisely, if
![]() $\{c,d\}$
is a nonseparating noncrossing annulus pair and
$\{c,d\}$
is a nonseparating noncrossing annulus pair and
![]() $e$
is a type 1 curve for
$e$
is a type 1 curve for
![]() $\{c,d\}$
, then
$\{c,d\}$
, then
![]() $\alpha (e)$
is a type 1 curve for the nonseparating noncrossing annulus pair
$\alpha (e)$
is a type 1 curve for the nonseparating noncrossing annulus pair
![]() $\{\alpha (c),\alpha (d)\}$
, and similarly for type 2 curves.
$\{\alpha (c),\alpha (d)\}$
, and similarly for type 2 curves.
We can also discuss Lemma 3.10 in an annular domain as well, so its proof is the same as in [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 2.7], and therefore we omit it.
We end this section by discussing how Propositions 3.1 and 3.2 can be derived from the lemmas in this section. For Proposition 3.1, each nonseparating bigon pair is a nonseparating noncrossing annulus pair
![]() $\{c,d\}$
that forms exactly one inessential curve bounding a disk and has the additional property that
$\{c,d\}$
that forms exactly one inessential curve bounding a disk and has the additional property that
![]() $c\cap d$
is a nondegenerate interval. Hence, by Lemmas 3.9 and 3.10, we can prove Proposition 3.1 by the same way as the case of orientable surfaces. Proposition 3.2 follows from Proposition 3.1, Lemma 3.7, and the following claim: two bigon pairs
$c\cap d$
is a nondegenerate interval. Hence, by Lemmas 3.9 and 3.10, we can prove Proposition 3.1 by the same way as the case of orientable surfaces. Proposition 3.2 follows from Proposition 3.1, Lemma 3.7, and the following claim: two bigon pairs
![]() $\{c,d\}$
and
$\{c,d\}$
and
![]() $\{c',d'\}$
form a linked sharing pair if and only if the following conditions hold.
$\{c',d'\}$
form a linked sharing pair if and only if the following conditions hold.
-
1. Each of
 $\{c,d'\}$
and
$\{c,d'\}$
and
 $\{c',d\}$
is a nondegenerate torus pair.
$\{c',d\}$
is a nondegenerate torus pair. -
2. There is a curve that forms a torus triple with both
 $\{c,d'\}$
and
$\{c,d'\}$
and
 $\{c',d\}$
.
$\{c',d\}$
.
The proof of claim is the same as the case of orientable surfaces.
4. Connectedness of fine arc graphs
In [Reference Long, Margalit, Pham, Verberne and Yao5], Long, Margalit, Pham, Verberne, and Yao introduced several fine arc graphs of orientable surfaces and proved their connectedness. In this section, we consider the fine arc graphs of nonorientable surfaces and prove their connectedness as well. The proofs for nonorientable surfaces are similar to those in [Reference Long, Margalit, Pham, Verberne and Yao5], but we include them for the convenience of the reader. Throughout this section, let
![]() $F$
be a compact surface with nonempty boundary
$F$
be a compact surface with nonempty boundary
![]() $\partial F \neq \emptyset$
.
$\partial F \neq \emptyset$
.
We define the fine arc graph
![]() ${\mathcal{A}^{\dagger }} (F)$
of
${\mathcal{A}^{\dagger }} (F)$
of
![]() $F$
. An arc
$F$
. An arc
![]() $a \colon [0,1] \to F$
is said to be simple if
$a \colon [0,1] \to F$
is said to be simple if
![]() $a$
is injective, proper if
$a$
is injective, proper if
![]() $a^{-1}(\partial F)=\{0,1\}$
, and essential if it is not homotopic to
$a^{-1}(\partial F)=\{0,1\}$
, and essential if it is not homotopic to
![]() $\partial F$
. We assume an arc to be simple, essential, and proper. We say that two arcs have disjoint interiors if they are disjoint away from
$\partial F$
. We assume an arc to be simple, essential, and proper. We say that two arcs have disjoint interiors if they are disjoint away from
![]() $\partial F$
. The fine arc graph
$\partial F$
. The fine arc graph
![]() ${\mathcal{A}^{\dagger }} (F)$
is the graph whose vertices are essential simple proper arcs in
${\mathcal{A}^{\dagger }} (F)$
is the graph whose vertices are essential simple proper arcs in
![]() $F$
and whose edges connect vertices with disjoint interiors. We say that two arcs are completely disjoint if they have no intersections (including at the boundary).
$F$
and whose edges connect vertices with disjoint interiors. We say that two arcs are completely disjoint if they have no intersections (including at the boundary).
Proposition 4.1 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Proposition 3.1]). For any
![]() $N=N_{g}^b$
with
$N=N_{g}^b$
with
![]() $b\gt 0$
, the graph
$b\gt 0$
, the graph
![]() ${\mathcal{A}^{\dagger }}(N)$
is connected.
${\mathcal{A}^{\dagger }}(N)$
is connected.
Proof. Since the arc graph
![]() $\mathcal{A}(N)$
is connected (see [Reference Kuno4, Corollary 1]), by considering the natural projection
$\mathcal{A}(N)$
is connected (see [Reference Kuno4, Corollary 1]), by considering the natural projection
![]() ${\mathcal{A}^{\dagger }}(N) \to \mathcal{A}(N)$
, it suffices to show the following: for every two isotopic essential simple proper arcs in
${\mathcal{A}^{\dagger }}(N) \to \mathcal{A}(N)$
, it suffices to show the following: for every two isotopic essential simple proper arcs in
![]() $N$
there exists a path in
$N$
there exists a path in
![]() ${\mathcal{A}^{\dagger }}(N)$
connecting them. Let
${\mathcal{A}^{\dagger }}(N)$
connecting them. Let
![]() $a,b \colon [0,1] \to N$
be two isotopic arcs and
$a,b \colon [0,1] \to N$
be two isotopic arcs and
![]() $H \colon [0,1] \times [0,1] \to N$
an isotopy from
$H \colon [0,1] \times [0,1] \to N$
an isotopy from
![]() $a$
to
$a$
to
![]() $b$
. For every
$b$
. For every
![]() $c \in{\mathcal{A}^{\dagger }}(N)$
, we define an open set
$c \in{\mathcal{A}^{\dagger }}(N)$
, we define an open set
![]() $I_c$
in
$I_c$
in
![]() $[0,1]$
by:
$[0,1]$
by:
where
![]() $a_t \;:\!=\; H(\cdot, t) \colon [0,1] \to N$
. We can find
$a_t \;:\!=\; H(\cdot, t) \colon [0,1] \to N$
. We can find
![]() $c_0,c_1,\dots, c_k \in{\mathcal{A}^{\dagger }}(N)$
such that
$c_0,c_1,\dots, c_k \in{\mathcal{A}^{\dagger }}(N)$
such that
-
•
 $[0,1] = I_{c_0} \cup I_{c_1} \cup \cdots \cup I_{c_k}$
,
$[0,1] = I_{c_0} \cup I_{c_1} \cup \cdots \cup I_{c_k}$
, -
•
 $0 \in I_{c_0}$
and
$0 \in I_{c_0}$
and
 $1 \in I_{c_k}$
, and
$1 \in I_{c_k}$
, and -
•
 $I_{c_i} \cap I_{c_j} \neq \emptyset$
if and only if
$I_{c_i} \cap I_{c_j} \neq \emptyset$
if and only if
 $|i-j| =1$
.
$|i-j| =1$
.
By taking
![]() $t_i \in I_{c_{i-1}} \cap I_{c_{i}}$
for each
$t_i \in I_{c_{i-1}} \cap I_{c_{i}}$
for each
![]() $i=1,\cdots, k$
, we obtain a path
$i=1,\cdots, k$
, we obtain a path
in
![]() ${\mathcal{A}^{\dagger }}(N)$
between
${\mathcal{A}^{\dagger }}(N)$
between
![]() $a$
and
$a$
and
![]() $b$
.
$b$
.
We say that an arc in
![]() $F$
is nonseparating if its complement in
$F$
is nonseparating if its complement in
![]() $F$
is connected. The fine nonseparating arc graph
$F$
is connected. The fine nonseparating arc graph
![]() $\mathcal{NA}^{\dagger } (F)$
is the subgraph of
$\mathcal{NA}^{\dagger } (F)$
is the subgraph of
![]() ${\mathcal{A}^{\dagger }}(F)$
spanned by the nonseparating arcs.
${\mathcal{A}^{\dagger }}(F)$
spanned by the nonseparating arcs.
Corollary 4.2 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Corollary 3.2]). For any
![]() $N=N_{g}^b$
with
$N=N_{g}^b$
with
![]() $b\gt 0$
, the graph
$b\gt 0$
, the graph
![]() $\mathcal{NA}^{\dagger }(N)$
is connected.
$\mathcal{NA}^{\dagger }(N)$
is connected.
Proof. Let
![]() $a,b \in \mathcal{NA}^{\dagger }(N)$
. By Proposition 4.1, there exists a path
$a,b \in \mathcal{NA}^{\dagger }(N)$
. By Proposition 4.1, there exists a path
in
![]() ${\mathcal{A}^{\dagger }}(N)$
between
${\mathcal{A}^{\dagger }}(N)$
between
![]() $a$
and
$a$
and
![]() $b$
. We will obtain a path in
$b$
. We will obtain a path in
![]() $\mathcal{NA}^{\dagger }(N)$
between
$\mathcal{NA}^{\dagger }(N)$
between
![]() $a$
and
$a$
and
![]() $b$
from the above path by removing or replacing
$b$
from the above path by removing or replacing
![]() $a_i$
as necessary. Assume that
$a_i$
as necessary. Assume that
![]() $a_i$
is separating for some
$a_i$
is separating for some
![]() $i$
. If
$i$
. If
![]() $a_{i-1}$
and
$a_{i-1}$
and
![]() $a_{i+1}$
lie in the other side of
$a_{i+1}$
lie in the other side of
![]() $a_i$
, then we remove
$a_i$
, then we remove
![]() $a_i$
. Otherwise, they lie in the same side of
$a_i$
. Otherwise, they lie in the same side of
![]() $a_i$
. Let
$a_i$
. Let
![]() $R$
be the subsurface obtained by cutting
$R$
be the subsurface obtained by cutting
![]() $N$
along
$N$
along
![]() $a_i$
and not including
$a_i$
and not including
![]() $a_{i-1}$
and
$a_{i-1}$
and
![]() $a_{i+1}$
. Then we can find a nonseparating arc
$a_{i+1}$
. Then we can find a nonseparating arc
![]() $a_i'$
in
$a_i'$
in
![]() $N$
which lie in
$N$
which lie in
![]() $R$
as follows. Since
$R$
as follows. Since
![]() $a_i$
is separating, its endpoints lie in the same component
$a_i$
is separating, its endpoints lie in the same component
![]() $d$
of
$d$
of
![]() $\partial N$
. If
$\partial N$
. If
![]() $R$
is planar, then
$R$
is planar, then
![]() $R$
contains some other component
$R$
contains some other component
![]() $d'$
of
$d'$
of
![]() $\partial N$
since
$\partial N$
since
![]() $a_i$
is essential; we can take
$a_i$
is essential; we can take
![]() $a_i'$
to be any arc in
$a_i'$
to be any arc in
![]() $R$
connecting
$R$
connecting
![]() $d$
to
$d$
to
![]() $d'$
. If
$d'$
. If
![]() $R$
has positive genus, then we can take
$R$
has positive genus, then we can take
![]() $a_i'$
to be any nonseparating arc in
$a_i'$
to be any nonseparating arc in
![]() $R$
connecting
$R$
connecting
![]() $d$
to itself. Therefore, by applying this operation to each separating arc
$d$
to itself. Therefore, by applying this operation to each separating arc
![]() $a_i$
, we obtain a path in
$a_i$
, we obtain a path in
![]() $\mathcal{NA}^{\dagger }(N)$
between
$\mathcal{NA}^{\dagger }(N)$
between
![]() $a$
and
$a$
and
![]() $b$
.
$b$
.
For a surface
![]() $F$
with positive genus and a connected component
$F$
with positive genus and a connected component
![]() $d_0$
of
$d_0$
of
![]() $\partial F$
, we will define the fine linked arc graph
$\partial F$
, we will define the fine linked arc graph
![]() $\mathcal{A}_{\textrm{Lk}}^{\dagger }(F,d_0)$
. Let
$\mathcal{A}_{\textrm{Lk}}^{\dagger }(F,d_0)$
. Let
![]() $a$
and
$a$
and
![]() $b$
be two vertices of
$b$
be two vertices of
![]() ${\mathcal{A}^{\dagger }}(F)$
whose interiors are disjoint arcs. We say that
${\mathcal{A}^{\dagger }}(F)$
whose interiors are disjoint arcs. We say that
![]() $a$
and
$a$
and
![]() $b$
are linked at
$b$
are linked at
![]() $d_0$
if all four endpoints lying in
$d_0$
if all four endpoints lying in
![]() $d_0$
and a curve parallel and sufficiently close to
$d_0$
and a curve parallel and sufficiently close to
![]() $d_0$
intersects the arcs alternately. We define
$d_0$
intersects the arcs alternately. We define
![]() $\mathcal{A}_{\textrm{Lk}}^{\dagger }(F,d_0)$
as the graph whose vertices are nonseparating simple proper arcs in
$\mathcal{A}_{\textrm{Lk}}^{\dagger }(F,d_0)$
as the graph whose vertices are nonseparating simple proper arcs in
![]() $F$
with both endpoints lying in
$F$
with both endpoints lying in
![]() $d_0$
and whose edges connect arcs with disjoint interiors that are linked at
$d_0$
and whose edges connect arcs with disjoint interiors that are linked at
![]() $d_0$
.
$d_0$
.
Corollary 4.3 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Corollary 3.3]). For any
![]() $N=N_{g}^b$
with
$N=N_{g}^b$
with
![]() ${g} \geq 1$
and
${g} \geq 1$
and
![]() $b\gt 0$
, and any component
$b\gt 0$
, and any component
![]() $d_0$
of
$d_0$
of
![]() $\partial N$
, the graph
$\partial N$
, the graph
![]() $\mathcal{A}_{\textrm{Lk}}^{\dagger }(N,d_0)$
is connected.
$\mathcal{A}_{\textrm{Lk}}^{\dagger }(N,d_0)$
is connected.
Proof. Let
![]() $a,b \in \mathcal{A}_{\textrm{Lk}}^{\dagger }(N,d_0)$
. By Corollary 4.2, there exists a path
$a,b \in \mathcal{A}_{\textrm{Lk}}^{\dagger }(N,d_0)$
. By Corollary 4.2, there exists a path
in
![]() $\mathcal{NA}^{\dagger }(N)$
. We can assume that the endpoints of each
$\mathcal{NA}^{\dagger }(N)$
. We can assume that the endpoints of each
![]() $a_i$
lie in
$a_i$
lie in
![]() $d_0$
. We will obtain a path from
$d_0$
. We will obtain a path from
![]() $a$
to
$a$
to
![]() $b$
in
$b$
in
![]() $\mathcal{A}_{\textrm{Lk}}^{\dagger }(N,d_0)$
from the above path as follows: for each pair
$\mathcal{A}_{\textrm{Lk}}^{\dagger }(N,d_0)$
from the above path as follows: for each pair
![]() $a_i$
and
$a_i$
and
![]() $a_{i+1}$
that are not linked, we find an arc
$a_{i+1}$
that are not linked, we find an arc
![]() $b_i$
that is linked with both
$b_i$
that is linked with both
![]() $a_i$
and
$a_i$
and
![]() $a_{i+1}$
, and insert
$a_{i+1}$
, and insert
![]() $b_i$
between
$b_i$
between
![]() $a_i$
and
$a_i$
and
![]() $a_{i+1}$
.
$a_{i+1}$
.
Assume that
![]() $a_i$
and
$a_i$
and
![]() $a_{i+1}$
are not linked. Then, a tubular neighborhood
$a_{i+1}$
are not linked. Then, a tubular neighborhood
![]() $A$
of
$A$
of
![]() $d_0$
in
$d_0$
in
![]() $N$
is divided into four components
$N$
is divided into four components
![]() $A_0$
,
$A_0$
,
![]() $A_1$
,
$A_1$
,
![]() $A_2$
, and
$A_2$
, and
![]() $A_3$
by arcs
$A_3$
by arcs
![]() $a_i$
and
$a_i$
and
![]() $a_{i+1}$
. Let
$a_{i+1}$
. Let
![]() $A_0$
and
$A_0$
and
![]() $A_2$
be those that are bounded by one arc of
$A_2$
be those that are bounded by one arc of
![]() $a_i$
and one arc of
$a_i$
and one arc of
![]() $a_{i+1}$
. It is sufficient to see that
$a_{i+1}$
. It is sufficient to see that
![]() $A_1$
and
$A_1$
and
![]() $A_3$
lie in the same component of
$A_3$
lie in the same component of
![]() $N \setminus (a_i \cup a_{i+1})$
; we can take
$N \setminus (a_i \cup a_{i+1})$
; we can take
![]() $b_i$
as an arc connecting
$b_i$
as an arc connecting
![]() $A_1$
and
$A_1$
and
![]() $A_3$
in
$A_3$
in
![]() $N \setminus (a_i \cup a_{i+1})$
. Note that this is obviously true if
$N \setminus (a_i \cup a_{i+1})$
. Note that this is obviously true if
![]() $N \setminus (a_i \cup a_{i+1})$
is connected.
$N \setminus (a_i \cup a_{i+1})$
is connected.
Suppose
![]() $N \setminus (a_i \cup a_{i+1})$
is not connected. Then both
$N \setminus (a_i \cup a_{i+1})$
is not connected. Then both
![]() $a_i$
and
$a_i$
and
![]() $a_{i+1}$
must pass through crosscaps an even number of times (if
$a_{i+1}$
must pass through crosscaps an even number of times (if
![]() $a_i$
or
$a_i$
or
![]() $a_{i+1}$
passes through crosscaps an odd number of times, then
$a_{i+1}$
passes through crosscaps an odd number of times, then
![]() $N \setminus (a_i \cup a_{i+1})$
would be connected). By cutting
$N \setminus (a_i \cup a_{i+1})$
would be connected). By cutting
![]() $N$
along
$N$
along
![]() $a_i \cup a_{i+1}$
, the boundary
$a_i \cup a_{i+1}$
, the boundary
![]() $d_0$
splits into three boundaries
$d_0$
splits into three boundaries
![]() $d_1$
,
$d_1$
,
![]() $d_2$
, and
$d_2$
, and
![]() $d_3$
so that
$d_3$
so that
![]() $A_i$
is attached to
$A_i$
is attached to
![]() $d_i$
for
$d_i$
for
![]() $i=1,2,3$
(
$i=1,2,3$
(
![]() $A_0$
is attached to
$A_0$
is attached to
![]() $d_2$
). It follows that
$d_2$
). It follows that
![]() $d_1$
and
$d_1$
and
![]() $d_3$
(and hence
$d_3$
(and hence
![]() $A_1$
and
$A_1$
and
![]() $A_3$
) must lie in the same components; otherwise, it contradicts the assumption that
$A_3$
) must lie in the same components; otherwise, it contradicts the assumption that
![]() $a_i$
and
$a_i$
and
![]() $a_{i+1}$
are nonseparating. This completes the proof.
$a_{i+1}$
are nonseparating. This completes the proof.
5. Automorphisms of the extended fine curve graphs
The goal of this section is to provide an outline of the proof of the following theorem:
Theorem 5.1 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Theorem 1.2]). Let
![]() $N$
be a closed nonorientable surface. Then, the natural map
$N$
be a closed nonorientable surface. Then, the natural map
![]() $\nu \colon \mathrm{Homeo}(N)\rightarrow \textrm{Aut}( \mathcal{EC}^{\dagger }(N) )$
is an isomorphism.
$\nu \colon \mathrm{Homeo}(N)\rightarrow \textrm{Aut}( \mathcal{EC}^{\dagger }(N) )$
is an isomorphism.
We define the extended fine curve graph
![]() $\mathcal{EC}^{\dagger }(N)$
of a closed nonorientable surface
$\mathcal{EC}^{\dagger }(N)$
of a closed nonorientable surface
![]() $N$
to be a graph whose vertices are all the essential simple closed curves in
$N$
to be a graph whose vertices are all the essential simple closed curves in
![]() $N$
or the inessential simple closed curves that bound a disk in
$N$
or the inessential simple closed curves that bound a disk in
![]() $N$
, and an edge is a pair of vertices which are disjoint in
$N$
, and an edge is a pair of vertices which are disjoint in
![]() $N$
. We emphasize that in our argument the vertex set of the extended fine curve graph
$N$
. We emphasize that in our argument the vertex set of the extended fine curve graph
![]() $\mathcal{EC}^{\dagger }(N)$
of any closed nonorientable surface
$\mathcal{EC}^{\dagger }(N)$
of any closed nonorientable surface
![]() $N$
does not contain any inessential curves bounding a Möbius band.
$N$
does not contain any inessential curves bounding a Möbius band.
Following the method of [Reference Long, Margalit, Pham, Verberne and Yao5], we use convergent sequences described below to prove Theorem 5.1. We see that the lemmas and corollaries corresponding to [Reference Long, Margalit, Pham, Verberne and Yao5, Section 4] also hold for nonorientable surfaces. We will only describe why they are valid for nonorientable surfaces and omit their proofs.
Let
![]() $N$
be a closed nonorientable surface of genus
$N$
be a closed nonorientable surface of genus
![]() $g$
. We say that a sequence of vertices
$g$
. We say that a sequence of vertices
![]() $(c_{i})$
of
$(c_{i})$
of
![]() $\mathcal{EC}^{\dagger }(N)$
converges to a point
$\mathcal{EC}^{\dagger }(N)$
converges to a point
![]() $x\in N$
if every neighborhood of
$x\in N$
if every neighborhood of
![]() $x$
contains all but finitely many of the corresponding curves to
$x$
contains all but finitely many of the corresponding curves to
![]() $c_{i}$
, and we write
$c_{i}$
, and we write
![]() $\mathrm{lim}(c_{i})=x$
. If
$\mathrm{lim}(c_{i})=x$
. If
![]() $(c_{i})$
is convergent, it must be that there exists
$(c_{i})$
is convergent, it must be that there exists
![]() $M\gt 0$
such that each
$M\gt 0$
such that each
![]() $c_{i}$
with
$c_{i}$
with
![]() $i\gt M$
bounds a disk in
$i\gt M$
bounds a disk in
![]() $N$
.
$N$
.
Since [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 4.1] is proved by a local argument in a surface, the same argument works also for nonorientable surfaces.
Lemma 5.2 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 4.1]). Let
![]() $N$
be a closed nonorientable surface, and let
$N$
be a closed nonorientable surface, and let
![]() $(x_{i})$
be a sequence of points in
$(x_{i})$
be a sequence of points in
![]() $N$
that converges to a point
$N$
that converges to a point
![]() $x\in N$
. Then, there exists a simple closed curve in
$x\in N$
. Then, there exists a simple closed curve in
![]() $N$
that contains infinitely many of the
$N$
that contains infinitely many of the
![]() $x_{i}$
.
$x_{i}$
.
Since the argument in [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 4.2] is compactness of surfaces, we can show the same result for nonorientable surfaces.
Lemma 5.3 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 4.2]). Let
![]() $N$
be a closed nonorientable surface. Automorphisms of
$N$
be a closed nonorientable surface. Automorphisms of
![]() $\mathcal{EC}^{\dagger }(N)$
preserve convergent sequences
$\mathcal{EC}^{\dagger }(N)$
preserve convergent sequences
We say that two convergent sequences of vertices of
![]() $\mathcal{EC}^{\dagger }(N)$
are coincident if they converge to the same point of
$\mathcal{EC}^{\dagger }(N)$
are coincident if they converge to the same point of
![]() $N$
. The interleave of two sequences
$N$
. The interleave of two sequences
![]() $(c_{i})$
and
$(c_{i})$
and
![]() $(d_{i})$
is a sequence
$(d_{i})$
is a sequence
![]() $c_{1}$
,
$c_{1}$
,
![]() $d_{1}$
,
$d_{1}$
,
![]() $c_{2}$
,
$c_{2}$
,
![]() $d_{2}$
,
$d_{2}$
,
![]() $\cdots$
. We have the following corollary of Lemma 5.3.
$\cdots$
. We have the following corollary of Lemma 5.3.
Corollary 5.4 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Corollary 4.3]). Let
![]() $N$
be a closed nonorientable surface. Let
$N$
be a closed nonorientable surface. Let
![]() $(c_{i})$
and
$(c_{i})$
and
![]() $(d_{i})$
be two convergent sequences of vertices of
$(d_{i})$
be two convergent sequences of vertices of
![]() $\mathcal{EC}^{\dagger }(N)$
. Then,
$\mathcal{EC}^{\dagger }(N)$
. Then,
![]() $(c_{i})$
and
$(c_{i})$
and
![]() $(d_{i})$
are coincident if and only if the interleave of
$(d_{i})$
are coincident if and only if the interleave of
![]() $(c_{i})$
and
$(c_{i})$
and
![]() $(d_{i})$
is convergent. In particular, automorphisms of
$(d_{i})$
is convergent. In particular, automorphisms of
![]() $\mathcal{EC}^{\dagger }(N)$
preserve the coincidence of convergent sequences.
$\mathcal{EC}^{\dagger }(N)$
preserve the coincidence of convergent sequences.
We say that a sequence
![]() $(c_{i}^{1})$
,
$(c_{i}^{1})$
,
![]() $(c_{i}^{2})$
,
$(c_{i}^{2})$
,
![]() $(c_{i}^{3})$
,
$(c_{i}^{3})$
,
![]() $\cdots$
of convergent sequences of vertices of
$\cdots$
of convergent sequences of vertices of
![]() $\mathcal{EC}^{\dagger }(N)$
converges if the sequence of limit points
$\mathcal{EC}^{\dagger }(N)$
converges if the sequence of limit points
![]() $\textrm{lim}(c_{i}^{1})$
,
$\textrm{lim}(c_{i}^{1})$
,
![]() $\textrm{lim}(c_{i}^{2})$
,
$\textrm{lim}(c_{i}^{2})$
,
![]() $\textrm{lim}(c_{i}^{3})$
,
$\textrm{lim}(c_{i}^{3})$
,
![]() $\cdots$
converges to a point
$\cdots$
converges to a point
![]() $x\in N$
. In this case, we say that the sequence converges to
$x\in N$
. In this case, we say that the sequence converges to
![]() $x$
.
$x$
.
Corollary 5.5 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Corollary 4.4]). Let
![]() $N$
be a closed nonorientable surface. Automorphisms of
$N$
be a closed nonorientable surface. Automorphisms of
![]() $\mathcal{EC}^{\dagger }(N)$
preserve convergent sequences of convergent sequences of vertices of
$\mathcal{EC}^{\dagger }(N)$
preserve convergent sequences of convergent sequences of vertices of
![]() $\mathcal{EC}^{\dagger }(N)$
.
$\mathcal{EC}^{\dagger }(N)$
.
We say that a vertex
![]() $c$
is a limit curve for a sequence
$c$
is a limit curve for a sequence
![]() $(c_{i})$
of vertices in
$(c_{i})$
of vertices in
![]() $\mathcal{EC}^{\dagger }(N)$
if
$\mathcal{EC}^{\dagger }(N)$
if
![]() $\textrm{lim}(c_{i})\in c$
.
$\textrm{lim}(c_{i})\in c$
.
Corollary 5.6 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Corollary 4.5]). Let
![]() $N$
be a closed nonorientable surface. Let
$N$
be a closed nonorientable surface. Let
![]() $c$
be a limit curve for a sequence
$c$
be a limit curve for a sequence
![]() $(c_{i})$
of vertices, and
$(c_{i})$
of vertices, and
![]() $\alpha$
an automorphism of
$\alpha$
an automorphism of
![]() $\mathcal{EC}^{\dagger }(N)$
. Then,
$\mathcal{EC}^{\dagger }(N)$
. Then,
![]() $\alpha (c)$
is a limit curve for
$\alpha (c)$
is a limit curve for
![]() $(\alpha (c_{i}))$
.
$(\alpha (c_{i}))$
.
We provide an outline of the proof of Theorem 5.1. We can prove the injectivity of
![]() $\nu$
as follows.
$\nu$
as follows.
Lemma 5.7 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 4.6]). Let
![]() $N$
be a closed nonorientable surface of genus
$N$
be a closed nonorientable surface of genus
![]() $g$
. The natural map
$g$
. The natural map
![]() $\nu \colon \mathrm{Homeo}(N)\rightarrow \mathrm{Aut}(\mathcal{EC}^{\dagger }(N))$
is injective.
$\nu \colon \mathrm{Homeo}(N)\rightarrow \mathrm{Aut}(\mathcal{EC}^{\dagger }(N))$
is injective.
Proof. We can prove the same as in [Reference Long, Margalit, Pham, Verberne and Yao5] as follows. Assume that
![]() $f \in \operatorname{Ker} \nu$
. For every
$f \in \operatorname{Ker} \nu$
. For every
![]() $x \in N$
, there exist two curves
$x \in N$
, there exist two curves
![]() $c,d \in \mathcal{EC}^{\dagger }(N)$
such that
$c,d \in \mathcal{EC}^{\dagger }(N)$
such that
![]() $c \cap d = \{x\}$
. Then,
$c \cap d = \{x\}$
. Then,
![]() $f(x)=f(c \cap d)=c \cap d = x$
and this implies that
$f(x)=f(c \cap d)=c \cap d = x$
and this implies that
![]() $f$
is the identity.
$f$
is the identity.
Therefore, it is sufficient to prove that
![]() $\nu$
is surjective. As in [Reference Long, Margalit, Pham, Verberne and Yao5], we can define
$\nu$
is surjective. As in [Reference Long, Margalit, Pham, Verberne and Yao5], we can define
![]() $\xi \colon \textrm{Aut}(\mathcal{EC}^{\dagger }(N)) \to \textrm{Homeo}(N)$
as follows: for
$\xi \colon \textrm{Aut}(\mathcal{EC}^{\dagger }(N)) \to \textrm{Homeo}(N)$
as follows: for
![]() $\alpha \in \textrm{Aut}(\mathcal{EC}^{\dagger }(N))$
, we define
$\alpha \in \textrm{Aut}(\mathcal{EC}^{\dagger }(N))$
, we define
![]() $\xi (\alpha ) \in \textrm{Homeo}(N)$
by
$\xi (\alpha ) \in \textrm{Homeo}(N)$
by
![]() $\xi (\alpha )(x)=\lim ( \alpha (c_i))$
, where
$\xi (\alpha )(x)=\lim ( \alpha (c_i))$
, where
![]() $(c_i)$
is a convergent sequence of
$(c_i)$
is a convergent sequence of
![]() $x \in N$
.
$x \in N$
.
As Claims 1 and 2 in the proof of [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 4.6], we can observe the following:
-
(a) If
 $\alpha \in \textrm{Aut}(\mathcal{EC}^{\dagger }(N))$
and
$\alpha \in \textrm{Aut}(\mathcal{EC}^{\dagger }(N))$
and
 $c \in \mathcal{EC}^{\dagger }(N)$
, then
$c \in \mathcal{EC}^{\dagger }(N)$
, then
 $\xi (\alpha )(c)=\alpha (c)$
.
$\xi (\alpha )(c)=\alpha (c)$
. -
(b) If
 $f \in \textrm{Homeo}(N)$
and
$f \in \textrm{Homeo}(N)$
and
 $c \in \mathcal{EC}^{\dagger }(N)$
, then
$c \in \mathcal{EC}^{\dagger }(N)$
, then
 $\nu (f)(c)=f(c)$
.
$\nu (f)(c)=f(c)$
.
We remark that (a) follows from Corollary 5.6 and (b) follow from the definition. By using (a) and (b), for every
![]() $\alpha \in \textrm{Aut}(\mathcal{EC}^{\dagger }(N))$
and every
$\alpha \in \textrm{Aut}(\mathcal{EC}^{\dagger }(N))$
and every
![]() $c \in \mathcal{EC}^{\dagger }(N)$
, we have
$c \in \mathcal{EC}^{\dagger }(N)$
, we have
This implies that
![]() $\nu (\xi (\alpha ))= \alpha$
and thus
$\nu (\xi (\alpha ))= \alpha$
and thus
![]() $\nu$
is surjective, and Theorem 5.1 holds.
$\nu$
is surjective, and Theorem 5.1 holds.
6. Automorphisms of the fine curve graph
In this section, we prove Theorem 1.1. By the same argument as in the proof of Lemma 5.7, the following lemma holds.
Lemma 6.1 (cf. [Reference Long, Margalit, Pham, Verberne and Yao5, Lemma 5.1]). Let
![]() $N$
be a closed nonorientable surface. The natural map
$N$
be a closed nonorientable surface. The natural map
![]() $\eta \colon \mathrm{Homeo}(N)\rightarrow \mathrm{Aut}(\mathcal{C}^{\dagger }(N))$
is injective.
$\eta \colon \mathrm{Homeo}(N)\rightarrow \mathrm{Aut}(\mathcal{C}^{\dagger }(N))$
is injective.
Before proving Theorem 1.1, we require the following notion. Let
![]() $\Gamma$
be a graph and
$\Gamma$
be a graph and
![]() $\Delta \subset \Gamma$
a subgraph. A map
$\Delta \subset \Gamma$
a subgraph. A map
![]() $E\colon \mathrm{Aut}(\Delta )\rightarrow \mathrm{Aut}(\Gamma )$
is an extension map if for any
$E\colon \mathrm{Aut}(\Delta )\rightarrow \mathrm{Aut}(\Gamma )$
is an extension map if for any
![]() $\varphi \in \mathrm{Aut}(\Delta )$
,
$\varphi \in \mathrm{Aut}(\Delta )$
,
![]() $E(\varphi )(\Delta )=\Delta$
, and
$E(\varphi )(\Delta )=\Delta$
, and
![]() $E(\varphi )|_{\Delta }=\varphi$
.
$E(\varphi )|_{\Delta }=\varphi$
.
We now prove Theorem 1.1, by the same strategy as the proof of [Reference Long, Margalit, Pham, Verberne and Yao5, Theorem 1.1].
Proof of Theorem 1.1. This proof has two steps. In the first step, we construct an extension homomorphism
![]() $\varepsilon \colon \mathrm{Aut}(\mathcal{C}^{\dagger }(N))\rightarrow \mathrm{Aut}(\mathcal{EC}^{\dagger }(N))$
, and in the second step, we complete the proof by using the extension homomorphism
$\varepsilon \colon \mathrm{Aut}(\mathcal{C}^{\dagger }(N))\rightarrow \mathrm{Aut}(\mathcal{EC}^{\dagger }(N))$
, and in the second step, we complete the proof by using the extension homomorphism
![]() $\varepsilon$
.
$\varepsilon$
.
Step 1. Let
![]() $\alpha \in \mathrm{Aut}(\mathcal{C}^{\dagger }(N))$
. We define
$\alpha \in \mathrm{Aut}(\mathcal{C}^{\dagger }(N))$
. We define
![]() $\hat{\alpha }\colon \mathcal{EC}^{\dagger }(N)\rightarrow \mathcal{EC}^{\dagger }(N)$
as follows. If
$\hat{\alpha }\colon \mathcal{EC}^{\dagger }(N)\rightarrow \mathcal{EC}^{\dagger }(N)$
as follows. If
![]() $c$
is an essential curve in
$c$
is an essential curve in
![]() $N$
, that is, if
$N$
, that is, if
![]() $c\in \mathcal{C}^{\dagger }(N)$
, then
$c\in \mathcal{C}^{\dagger }(N)$
, then
![]() $\hat{\alpha }(c)=\alpha (c)$
. If
$\hat{\alpha }(c)=\alpha (c)$
. If
![]() $e$
is an inessential curve which bounds a disk in
$e$
is an inessential curve which bounds a disk in
![]() $N$
, then we choose a nonseparating bigon pair
$N$
, then we choose a nonseparating bigon pair
![]() $\{c,d\}$
that determines
$\{c,d\}$
that determines
![]() $e$
and define
$e$
and define
![]() $\hat{\alpha }(e)$
to be an inessential curve bounding a disk determined by the nonseparating bigon pair
$\hat{\alpha }(e)$
to be an inessential curve bounding a disk determined by the nonseparating bigon pair
![]() $\{\alpha (c), \alpha (d)\}$
; this correspondence makes sense because of Proposition 3.1.
$\{\alpha (c), \alpha (d)\}$
; this correspondence makes sense because of Proposition 3.1.
First, we verify
![]() $\hat{\alpha }$
is well defined and an automorphism of
$\hat{\alpha }$
is well defined and an automorphism of
![]() $\mathcal{EC}^{\dagger }(N)$
. Suppose that
$\mathcal{EC}^{\dagger }(N)$
. Suppose that
![]() $\{c',d'\}$
is another nonseparating bigon pair that determines
$\{c',d'\}$
is another nonseparating bigon pair that determines
![]() $e$
. It follows from Corollary 4.3 that there exists a sequence of bigon pairs:
$e$
. It follows from Corollary 4.3 that there exists a sequence of bigon pairs:
where each pair
![]() $\{\{c_{i},d_{i}\}, \{c_{i+1}, d_{i+1}\}\}$
(
$\{\{c_{i},d_{i}\}, \{c_{i+1}, d_{i+1}\}\}$
(
![]() $i=0,1,\cdots, n-1$
) is a linked sharing pair for
$i=0,1,\cdots, n-1$
) is a linked sharing pair for
![]() $e$
. It follows from Proposition 3.2 that
$e$
. It follows from Proposition 3.2 that
![]() $\{\alpha (c'), \alpha (d')\}$
also determines the inessential curve
$\{\alpha (c'), \alpha (d')\}$
also determines the inessential curve
![]() $\hat{\alpha }(e)$
bounding a disk, and we see that
$\hat{\alpha }(e)$
bounding a disk, and we see that
![]() $\hat{\alpha }$
is well defined.
$\hat{\alpha }$
is well defined.
Next, we show that
![]() $\hat{\alpha }$
is an automorphism of
$\hat{\alpha }$
is an automorphism of
![]() $\mathcal{EC}^{\dagger }(N)$
. Since
$\mathcal{EC}^{\dagger }(N)$
. Since
![]() $\hat{\alpha }$
is a bijection on the set of vertices of
$\hat{\alpha }$
is a bijection on the set of vertices of
![]() $\mathcal{EC}^{\dagger }(N)$
it suffices to show that
$\mathcal{EC}^{\dagger }(N)$
it suffices to show that
![]() $\hat{\alpha }$
maps any edge to an edge.
$\hat{\alpha }$
maps any edge to an edge.
Let
![]() $a_{1}$
and
$a_{1}$
and
![]() $a_{2}$
be two distinct essential curves. Then
$a_{2}$
be two distinct essential curves. Then
![]() $\hat{\alpha }(a_{1})=\alpha (a_{1})$
and
$\hat{\alpha }(a_{1})=\alpha (a_{1})$
and
![]() $\hat{\alpha }(a_{2})=\alpha (a_{2})$
, and so
$\hat{\alpha }(a_{2})=\alpha (a_{2})$
, and so
![]() $\hat{\alpha }(a_{1})$
and
$\hat{\alpha }(a_{1})$
and
![]() $\hat{\alpha }(a_{2})$
form an edge if and only if
$\hat{\alpha }(a_{2})$
form an edge if and only if
![]() $a_{1}$
and
$a_{1}$
and
![]() $a_{2}$
form an edge. For the case where an edge is spanned by an essential curve
$a_{2}$
form an edge. For the case where an edge is spanned by an essential curve
![]() $c$
and an inessential curve
$c$
and an inessential curve
![]() $e$
bounding a disk, we claim that there exists a nonseparating bigon pair
$e$
bounding a disk, we claim that there exists a nonseparating bigon pair
![]() $\{d_{1}, d_{2}\}$
that determines
$\{d_{1}, d_{2}\}$
that determines
![]() $e$
and is disjoint from
$e$
and is disjoint from
![]() $c$
. In fact, if
$c$
. In fact, if
![]() $c$
is a separating curve in
$c$
is a separating curve in
![]() $N$
, we set the two connected components
$N$
, we set the two connected components
![]() $N'$
and
$N'$
and
![]() $N''$
of
$N''$
of
![]() $N\setminus c$
, and we suppose that
$N\setminus c$
, and we suppose that
![]() $e$
lies in
$e$
lies in
![]() $N'$
. Since
$N'$
. Since
![]() $c$
is essential and
$c$
is essential and
![]() $N$
is a closed nonorientable surface, the genera of
$N$
is a closed nonorientable surface, the genera of
![]() $N'$
and
$N'$
and
![]() $N''$
are at least
$N''$
are at least
![]() $2$
. Hence, we can take two-sided (note that bigon pairs are constructed by only two-sided curves) nonseparating curves
$2$
. Hence, we can take two-sided (note that bigon pairs are constructed by only two-sided curves) nonseparating curves
![]() $d_{1}$
and
$d_{1}$
and
![]() $d_{2}$
on the component
$d_{2}$
on the component
![]() $N'$
containing
$N'$
containing
![]() $e$
so that the pair
$e$
so that the pair
![]() $\{d_{1}, d_{2}\}$
is a bigon pair that determines
$\{d_{1}, d_{2}\}$
is a bigon pair that determines
![]() $e$
. If
$e$
. If
![]() $c$
is a nonseparating curve in
$c$
is a nonseparating curve in
![]() $N$
, the surface
$N$
, the surface
![]() $F$
obtained by cutting
$F$
obtained by cutting
![]() $N$
along
$N$
along
![]() $c$
is homeomorphic to one of
$c$
is homeomorphic to one of
![]() $N_{{g}-1}^{1}$
,
$N_{{g}-1}^{1}$
,
![]() $N_{{g}-2}^{2}$
,
$N_{{g}-2}^{2}$
,
![]() $S_{\frac{{g}-1}{2}}^{1}$
, or
$S_{\frac{{g}-1}{2}}^{1}$
, or
![]() $S_{\frac{{g}-2}{2}}^{2}$
(see Subsection 2.1). Since we assume that the genus of
$S_{\frac{{g}-2}{2}}^{2}$
(see Subsection 2.1). Since we assume that the genus of
![]() $N$
is at least
$N$
is at least
![]() $4$
, we can take two-sided nonseparating curves
$4$
, we can take two-sided nonseparating curves
![]() $d_{1}$
and
$d_{1}$
and
![]() $d_{2}$
on the surface
$d_{2}$
on the surface
![]() $F$
so that the pair
$F$
so that the pair
![]() $\{d_{1}, d_{2}\}$
is a bigon pair that determines
$\{d_{1}, d_{2}\}$
is a bigon pair that determines
![]() $e$
, as desired.
$e$
, as desired.

Figure 1. Bigon pair for disjoint inessential curves bounding a disk in the nested case (left) and the unnested case (right).
For the case where two inessential curves
![]() $e$
and
$e$
and
![]() $f$
that bound a disk form an edge, similar to the case of orientable surfaces we claim that two inessential curves
$f$
that bound a disk form an edge, similar to the case of orientable surfaces we claim that two inessential curves
![]() $e$
and
$e$
and
![]() $f$
bounding a disk are disjoint if and only if the following holds up to relabeling
$f$
bounding a disk are disjoint if and only if the following holds up to relabeling
![]() $e$
and
$e$
and
![]() $f$
: for every nonseparating bigon pair
$f$
: for every nonseparating bigon pair
![]() $\{c,d\}$
that determines
$\{c,d\}$
that determines
![]() $e$
, there is a bigon pair
$e$
, there is a bigon pair
![]() $\{c',d'\}$
that determines
$\{c',d'\}$
that determines
![]() $f$
and is disjoint from
$f$
and is disjoint from
![]() $e$
. The forward direction is proved by direct construction (see Figure 1), and note that since the genus of
$e$
. The forward direction is proved by direct construction (see Figure 1), and note that since the genus of
![]() $N$
is at least
$N$
is at least
![]() $4$
,
$4$
,
![]() $N$
has a subsurface homeomorphic to an orientable subsurface of genus
$N$
has a subsurface homeomorphic to an orientable subsurface of genus
![]() $1$
. For the other direction, we assume that two inessential curves
$1$
. For the other direction, we assume that two inessential curves
![]() $e$
and
$e$
and
![]() $f$
that bound a disk intersect. We choose an intersection point
$f$
that bound a disk intersect. We choose an intersection point
![]() $x\in e\cap f$
. We can take a nonseparating bigon pair
$x\in e\cap f$
. We can take a nonseparating bigon pair
![]() $\{c,d\}$
that determines
$\{c,d\}$
that determines
![]() $e$
where
$e$
where
![]() $x$
is one of the vertices of the bigon. Let
$x$
is one of the vertices of the bigon. Let
![]() $\{c',d'\}$
be any bigon pair that determines
$\{c',d'\}$
be any bigon pair that determines
![]() $f$
. Then
$f$
. Then
![]() $x\in f\subset c'\cup d'$
, and so
$x\in f\subset c'\cup d'$
, and so
![]() $c'\cup d'$
intersects
$c'\cup d'$
intersects
![]() $c$
, as desired. By this claim, we see that
$c$
, as desired. By this claim, we see that
![]() $\hat{\alpha }$
preserves the set of edges spanned by two inessential curves bounding a disk. Therefore, we see that
$\hat{\alpha }$
preserves the set of edges spanned by two inessential curves bounding a disk. Therefore, we see that
![]() $\hat{\alpha }$
is an automorphism of
$\hat{\alpha }$
is an automorphism of
![]() $\mathcal{EC}^{\dagger }(N)$
, in particular
$\mathcal{EC}^{\dagger }(N)$
, in particular
![]() $\hat{\alpha }$
is an automorphism of
$\hat{\alpha }$
is an automorphism of
![]() $\mathcal{C}^{\dagger }(N)$
.
$\mathcal{C}^{\dagger }(N)$
.
By the definition of
![]() $\varepsilon \colon \mathrm{Aut}(\mathcal{C}^{\dagger }(N))\rightarrow \mathrm{Aut}(\mathcal{EC}^{\dagger }(N))$
given by
$\varepsilon \colon \mathrm{Aut}(\mathcal{C}^{\dagger }(N))\rightarrow \mathrm{Aut}(\mathcal{EC}^{\dagger }(N))$
given by
![]() $\varepsilon (\alpha )=\hat{\alpha }$
, we have the desired extension map.
$\varepsilon (\alpha )=\hat{\alpha }$
, we have the desired extension map.
Step 2. Recall that
![]() $\eta \colon \mathrm{Homeo}(N)\rightarrow \mathrm{Aut}(\mathcal{C}^{\dagger }(N))$
and
$\eta \colon \mathrm{Homeo}(N)\rightarrow \mathrm{Aut}(\mathcal{C}^{\dagger }(N))$
and
![]() $\nu \colon \mathrm{Homeo}(N)\rightarrow \mathrm{Aut}(\mathcal{EC}^{\dagger }(N))$
are the natural homomorphisms. By Theorem 5.1, we see that
$\nu \colon \mathrm{Homeo}(N)\rightarrow \mathrm{Aut}(\mathcal{EC}^{\dagger }(N))$
are the natural homomorphisms. By Theorem 5.1, we see that
![]() $\nu$
is an isomorphism. Let
$\nu$
is an isomorphism. Let
![]() $\varepsilon$
be the extension homomorphism constructed in the first step.
$\varepsilon$
be the extension homomorphism constructed in the first step.
As with (b) in the previous section, the following holds by definition:
-
(c) If
 $f \in \textrm{Homeo}(N)$
and
$f \in \textrm{Homeo}(N)$
and
 $c \in \mathcal{C}^{\dagger }(N)$
, then
$c \in \mathcal{C}^{\dagger }(N)$
, then
 $\eta (f)(c)=f(c)$
.
$\eta (f)(c)=f(c)$
.
By (a) and (c), for every
![]() $\alpha \in \textrm{Aut}(\mathcal{C}^{\dagger }(N))$
and every
$\alpha \in \textrm{Aut}(\mathcal{C}^{\dagger }(N))$
and every
![]() $c \in \mathcal{C}^{\dagger }(N)$
, we have
$c \in \mathcal{C}^{\dagger }(N)$
, we have
This implies that
![]() $\eta (\xi (\varepsilon (\alpha )))= \alpha$
and thus
$\eta (\xi (\varepsilon (\alpha )))= \alpha$
and thus
![]() $\eta$
is surjective. Since
$\eta$
is surjective. Since
![]() $\eta$
is injective by Lemma 6.1, we have finished the proof.
$\eta$
is injective by Lemma 6.1, we have finished the proof.
Remark 6.2. In the definition of
![]() $\mathcal{EC}^{\dagger }(N)$
, we excluded curves that bound a Möbius band and allowed only those that bound a disk as inessential curves. This is done to avoid the difficulty of including curves that bound a Möbius band, and it is sufficient for the proof of our main theorem.
$\mathcal{EC}^{\dagger }(N)$
, we excluded curves that bound a Möbius band and allowed only those that bound a disk as inessential curves. This is done to avoid the difficulty of including curves that bound a Möbius band, and it is sufficient for the proof of our main theorem.
Remark 6.3. In the part where we verify
![]() $\hat{\alpha }$
is a bijection for the edges between one essential curve and one inessential curve bounding a disk in the proof of Theorem 1.1, if the genus
$\hat{\alpha }$
is a bijection for the edges between one essential curve and one inessential curve bounding a disk in the proof of Theorem 1.1, if the genus
![]() $g$
of a closed nonorientable surface is at most
$g$
of a closed nonorientable surface is at most
![]() $3$
, we cannot take a bigon pair
$3$
, we cannot take a bigon pair
![]() $\{d_{1},d_{2}\}$
that is disjoint from
$\{d_{1},d_{2}\}$
that is disjoint from
![]() $c$
in the case where
$c$
in the case where
![]() $c$
is nonseparating. In fact, in our definition of bigon pairs
$c$
is nonseparating. In fact, in our definition of bigon pairs
![]() $\{d_{1},d_{2}\}$
, the curves
$\{d_{1},d_{2}\}$
, the curves
![]() $d_{1}$
and
$d_{1}$
and
![]() $d_{2}$
are two-sided curves, and by Proposition 3.1 we see that automorphisms of the fine curve graph
$d_{2}$
are two-sided curves, and by Proposition 3.1 we see that automorphisms of the fine curve graph
![]() $\mathcal{C}^{\dagger }(N)$
preserve “nonseparating” bigon pairs. Therefore, we should take two-sided and nonseparating curves
$\mathcal{C}^{\dagger }(N)$
preserve “nonseparating” bigon pairs. Therefore, we should take two-sided and nonseparating curves
![]() $d_{1}$
and
$d_{1}$
and
![]() $d_{2}$
on the surface
$d_{2}$
on the surface
![]() $F$
obtained by cutting
$F$
obtained by cutting
![]() $N$
along
$N$
along
![]() $c$
, which is homeomorphic to
$c$
, which is homeomorphic to
![]() $N_{{g}-1}^{1}$
,
$N_{{g}-1}^{1}$
,
![]() $N_{{g}-2}^{2}$
,
$N_{{g}-2}^{2}$
,
![]() $S_{\frac{{g}-1}{2}}^{1}$
, or
$S_{\frac{{g}-1}{2}}^{1}$
, or
![]() $S_{\frac{{g}-2}{2}}^{2}$
. If
$S_{\frac{{g}-2}{2}}^{2}$
. If
![]() ${g} \leq 3$
,
${g} \leq 3$
,
![]() $F$
is homeomorphic to one of
$F$
is homeomorphic to one of
![]() $N_{1}^{1}$
,
$N_{1}^{1}$
,
![]() $N_{1}^{2}$
,
$N_{1}^{2}$
,
![]() $S_{0}^{1}$
, or
$S_{0}^{1}$
, or
![]() $S_{0}^{2}$
, and we can not take two-sided essential curves in these surfaces (see [Reference Atalan and Korkmaz1, Section 2.4]).
$S_{0}^{2}$
, and we can not take two-sided essential curves in these surfaces (see [Reference Atalan and Korkmaz1, Section 2.4]).
Acknowledgements
The authors wish to express their great appreciation to Genki Omori for valuable comments. They are also very grateful to the referee for carefully reading the manuscript and providing comments that helped us to improve the quality of the paper.
Funding statement
The first author is supported by JST-Mirai Program Grant Number JPMJMI22G1 and JSPS KAKENHI Grant number JP24K16921. The second author is supported by JSPS KAKENHI, grant number 21K13791.