No CrossRef data available.
Article contents
Arens regularity and retractions
Published online by Cambridge University Press: 18 May 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper a characterisation of the regularity of a normed algebra A is given in terms of retractions onto A** from A4*. The second dual A** of a normed algebra A possesses two natural Banach algebra multiplications, say ° and *. Each of ° and * extends the original algebra multiplication on A; see (2). An algebra A is called regular if and only if F * G = F ° G for all F, G ∈ A**. See (1). The existing results in the Arens regularity theory can be found in a recent survey (2). Denoting the nth dual of A by An*, and en the natural embedding of An* in its second dual A(n+2)*, we can naturally represent the second dual A** of A as a Banach space retract of A4* in two different ways:
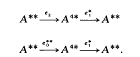
Our main results say that A** is in fact a Banach algebra retract of A4* (i.e. the maps involved are homomorphisms) in either of these cases if and only if A is regular.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1983
References
REFERENCES
2.Duncan, J. and Hosseinian, S. A. R., The second dual of a Banach algebra. Proc. Roy. Soc. Edinburgh 84(A), (1979), 309–325.CrossRefGoogle Scholar
3.Young, N. J., Periodicity of functionals and representations of normed algebras on reflexive spaces. Proc. Edinburgh Math. Soc, (2) 20, (1976), 99–120.Google Scholar
You have
Access