Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-27T19:44:44.906Z Has data issue: false hasContentIssue false
  • English
  • Français

AN INVARIANT OF LEGENDRIAN AND TRANSVERSE LINKS FROM OPEN BOOK DECOMPOSITIONS OF CONTACT 3-MANIFOLDS

Part of: Low-dimensional topology Differential topology

Published online by Cambridge University Press:  04 August 2020

ALBERTO CAVALLO
ALBERTO CAVALLO*
Affiliation:
Alfr´ed R´enyi Institute of Mathematics, Budapest 1053, Hungary, e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a generalization of the Lisca–Ozsváth–Stipsicz–Szabó Legendrian invariant 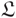${\mathfrak L}$ to links in every rational homology sphere, using the collapsed version of link Floer homology. We represent a Legendrian link L in a contact 3-manifold 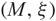${(M,\xi)}$ with a diagram D, given by an open book decomposition of 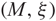${(M,\xi)}$ adapted to L, and we construct a chain complex 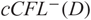${cCFL^-(D)}$ with a special cycle in it denoted by 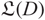${\mathfrak L(D)}$ . 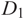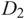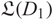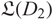Then, given two diagrams ${D_1}$ and ${D_2}$ which represent Legendrian isotopic links, we prove that there is a map between the corresponding chain complexes that induces an isomorphism in homology and sends ${\mathfrak L(D_1)}$ into ${\mathfrak L(D_2)}$ . Moreover, a connected sum formula is also proved and we use it to give some applications about non-loose Legendrian links; that are links such that the restriction of 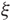${\xi}$ on their complement is tight.

MSC classification

Primary: 57M25: Knots and links in $S^3$
Secondary: 57R17: Symplectic and contact topology
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 2 , May 2021 , pp. 451 - 483
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baldwin, J., Vela-Vick, D. S. and Vértesi, V., On the equivalence of Legendrian and transverse invariants in knot Floer homology, Geom. Topol. 17(2) (2013), 925–974.CrossRefGoogle Scholar
Cavallo, A., On loose Legendrian knots in rational homology spheres, Topology Appl. 235 (2018), 339–345.CrossRefGoogle Scholar
Colin, V., Chirurgies d’indice un et isotopies de sphères dans les variétés de contact tendues, C. R. Acad. Sci. Paris Sér. I Math. 324 (1997), 659–663.CrossRefGoogle Scholar
Dymara, K., Legendrian knots in overtwisted contact structures on ${S^3}$ , Ann. Global Anal. Geom. 19(3) (2001), 293–305.Google Scholar
Eliashberg, Y., Classification of overtwisted contact structures on 3-manifolds, Invent. Math. 98(3) (1989), 623–637.CrossRefGoogle Scholar
Etnyre, J., Legendrian and Transversal Knots. Handbook of Knot Theory (Elsevier B. V., Amsterdam, 2005), 105–185.Google Scholar
Etnyre, J., Lectures on Open Book Decompositions and Contact Structures, Clay Mathematics Proceedings, vol. 5 (American Mathematical Society, Providence, RI, 2006), 103–141.Google Scholar
Etnyre, J. and Honda, K., Knots and contact geometry I: torus knots and the figure eight, J. Sympl. Geom. 1(1) (2001), 63–120.CrossRefGoogle Scholar
Etnyre, J. and Honda, K., On connected sums and Legendrian knots, Adv. Math. 179(1) (2003), 59–74.CrossRefGoogle Scholar
Giroux, E., Géométrie de contact: de la dimension trois vers les dimensions supérieures, in Proceedings of the International Congress of Mathematicians, vol. II (Higher Ed. Press, Beijing, 2002), 405–414.Google Scholar
Honda, K., Kazez, W. and Matić, G., On the contact class in Heegaard Floer homology, J. Diff. Geom. 83(2) (2009), 289–311.Google Scholar
Juhász, A., Miller, M. and Zemke, I., Transverse invariants and exotic surfaces in the 4-ball, arXiv:2001.07191.Google Scholar
Juhász, A., Thurston, D. and Zemke, I., Naturality and mapping class groups in Heegaard Floer homology, Mem. Am. Math. Soc. (to appear), arXiv:1210.4996.Google Scholar
Lisca, P., Ozsváth, P., Stipsicz, A. and Szabó, Z., Heegaard Floer invariants of Legendrian knots in contact three-manifolds, J. Eur. Math. Soc. 11(6) (2009), 1307–1363.CrossRefGoogle Scholar
Ozsváth, P. and Stipsicz, A., Contact surgeries and the transverse invariant in knot Floer homology, J. Inst. Math. Jussieu 9(3) (2010), 601–632.CrossRefGoogle Scholar
Ozsváth, P., Stipsicz, A. and Szabó, Z., Grid Homology for Knots and Links, AMS, Mathematical Surveys and Monographs, vol. 208 (2015).Google Scholar
Ozsváth, P. and Szabó, Z., Absolutely graded Floer homologies and intersection forms for four-manifolds with boundary, Adv. Math. 173(2) (2003), 179–261.CrossRefGoogle Scholar
Ozsváth, P. and Szabó, Z., Holomorphic disks and topological invariants of closed three-manifolds, Ann. Math. (2), 159(3) (2004), 1159–1245.CrossRefGoogle Scholar
Ozsváth, P. and Szabó, Z., Holomorphic disks and knot invariants, Adv. Math. 186(1) (2004), 58–116.CrossRefGoogle Scholar
Ozsváth, P. and Szabó, Z., Heegaard Floer homology and contact structures, Duke Math. J. 129(1) (2005), 39–61.CrossRefGoogle Scholar
Ozsváth, P. and Szabó, Z., Holomorphic disks, link invariants and the multi-variable Alexander polynomial, Algebr. Geom. Topol. 8(2) (2008), 615–692.CrossRefGoogle Scholar
Plamenevskaya, O., A combinatorial description of the Heegaard Floer contact invariant, Algebr. Geom. Topol. 7 (2007), 1201–1209.CrossRefGoogle Scholar
Rasmussen, J., Floer homology and knot complements, PhD Thesis (Harvard University, 2003).Google Scholar
Turaev, V., Torsions of 3-Manifolds , Geometry and Topology Monographs, vol. 4 (Geometry and Topology Publications, Coventry, 2002).Google Scholar