An infinitesimal proof of the implicit function theorem

Extract

We give a short and constructive proof of the general (multi-dimensional) Implicit Function Theorem (IFT), using infinitesimal (i.e. nonstandard) methods to implement our basic intuition about the result. Here is the statement of the IFT, quoted from [4];

Theorem. Let A ⊂ ℝⁿ × ℝ^mbe an open set and let F:A → ℝ be a function of class C^p (p≥1). Suppose that (x_O, y_O) ε A with F(x_O, y_O) = 0 (x_O ε ℝⁿ, y_O ε ℝ^m) and that the Jacobian determinant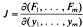is not zero at (x_O, y_O). Then there is an open neighbourhood U of x_O and a unique function f:U→ ℝ_mwith

F(x, f(x)) = 0

for all x ε U. Moreover, f is of class C^p.